蓝桥杯 --- 双指针、BFS与图论（习题）

1240. 完全二叉树的权值

给定一棵包含 N 个节点的完全二叉树，树上每个节点都有一个权值，按从上到下、从左到右的顺序依次是 A1,A2,⋅⋅⋅AN，如下图所示：

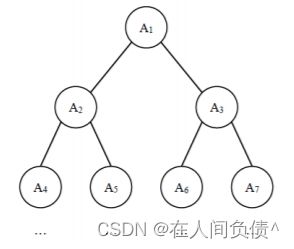
现在小明要把相同深度的节点的权值加在一起，他想知道哪个深度的节点权值之和最大？

如果有多个深度的权值和同为最大，请你输出其中最小的深度。

注：根的深度是 1。

输入格式
第一行包含一个整数 N。

第二行包含 N 个整数 A1,A2,⋅⋅⋅AN。

输出格式
输出一个整数代表答案。

数据范围

1≤N≤105 ,
−10⁵≤Ai≤10⁵

输入样例：

7
1 6 5 4 3 2 1

输出样例：

2

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include

#define x first
#define y second

using namespace std;
typedef long long ll;
typedef pair<int, int> PII;
const int N = 101000;
const int MOD = 1000000007;
const int INF = 0x3f3f3f3f;

int gcd(int a, int b){return b ? gcd(b, a % b) : a;}

int n;
ll a[N];

int main()
{
	cin >> n;
	for(int i = 1; i <= n; i ++ ) cin >> a[i];
	int maxx = -INF, flag = -1, idx = 1;
	for(int i = 1; i <= n; i *= 2 ) {
		ll sum = 0;
		for(int j = i; j <= i * 2 - 1 && j <= n; j ++ ) {
			sum += a[j];
		}
		if(sum > maxx) {
			maxx = sum;
			flag = idx;
		}
		idx ++ ;
	}
	cout << flag << endl;
	
	return 0;
}

1096. 地牢大师

你现在被困在一个三维地牢中，需要找到最快脱离的出路！

地牢由若干个单位立方体组成，其中部分不含岩石障碍可以直接通过，部分包含岩石障碍无法通过。

向北，向南，向东，向西，向上或向下移动一个单元距离均需要一分钟。

你不能沿对角线移动，迷宫边界都是坚硬的岩石，你不能走出边界范围。

请问，你有可能逃脱吗？

如果可以，需要多长时间？

输入格式
输入包含多组测试数据。

每组数据第一行包含三个整数 L,R,C 分别表示地牢层数，以及每一层地牢的行数和列数。

接下来是 L 个 R 行 C 列的字符矩阵，用来表示每一层地牢的具体状况。

每个字符用来描述一个地牢单元的具体状况。

其中, 充满岩石障碍的单元格用”#”表示，不含障碍的空单元格用”.”表示，你的起始位置用”S”表示，终点用”E”表示。

每一个字符矩阵后面都会包含一个空行。

当输入一行为”0 0 0”时，表示输入终止。

输出格式
每组数据输出一个结果，每个结果占一行。

如果能够逃脱地牢，则输出”Escaped in x minute(s).”，其中X为逃脱所需最短时间。

如果不能逃脱地牢，则输出”Trapped!”。

数据范围

1≤L,R,C≤100

输入样例：

3 4 5
S....
.###.
.##..
###.#

#####
#####
##.##
##...

#####
#####
#.###
####E

1 3 3
S##
#E#
###

0 0 0

输出样例：

Escaped in 11 minute(s).
Trapped!

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include

#define x first
#define y second

using namespace std;
typedef long long ll;
typedef pair<int, int> PII;
const int N = 110;
const int MOD = 1000000007;
const int INF = 0x3f3f3f3f;

int gcd(int a, int b){return b ? gcd(b, a % b) : a;}

int l, r, c;
char g[N][N][N];
int dist[N][N][N];

int dx[] = {0, 0, 1, 0, -1, 0};
int dy[] = {0, 0, 0, 1, 0, -1};
int dz[] = {1, -1, 0, 0, 0, 0};

struct Node{
	int z, x, y;
};

int bfs(int z, int x, int y) {
	queue<Node> q;
	q.push({z, x, y});
	dist[z][x][y] = 0;
	while(!q.empty()) {
		Node t = q.front();
		q.pop();
		for(int i = 0; i < 6; i ++ ) {
			int zz = t.z + dz[i];
			int xx = t.x + dx[i];
			int yy = t.y + dy[i];
			if(zz < 0 || zz >= l || xx < 0 || xx >= r || yy < 0 || yy >= c) continue;
			if(dist[zz][xx][yy] != -1) continue;
			if(g[zz][xx][yy] == '#') continue;
			dist[zz][xx][yy] = dist[t.z][t.x][t.y] + 1;
			if(g[zz][xx][yy] == 'E') return dist[zz][xx][yy];
			q.push({zz, xx, yy});
		}
	}
	return -1;
}

int main()
{	
	while(1) {
		memset(dist, -1, sizeof dist);
		cin >> l >> r >> c;
		if(l == 0 &&r == 0 && c == 0) break;
		int x, y, z;
		for(int i = 0; i < l; i ++ ) {
			for(int j = 0; j < r; j ++ ) {
				for(int k = 0; k < c; k ++ ) {
					cin >> g[i][j][k];
					if(g[i][j][k] == 'S') {
						z = i;
						x = j;
						y = k;
					}
				}
			}
		}	
		int res = bfs(z, x, y);
		if(res != -1) printf("Escaped in %d minute(s).\n",res);
		else cout << "Trapped!" << endl;
	}	
	
	return 0;
}

1233. 全球变暖

你有一张某海域 N×N 像素的照片，”.”表示海洋、”#”表示陆地，如下所示：

.......
.##....
.##....
....##.
..####.
...###.
.......

其中”上下左右”四个方向上连在一起的一片陆地组成一座岛屿，例如上图就有2 座岛屿。

由于全球变暖导致了海面上升，科学家预测未来几十年，岛屿边缘一个像素的范围会被海水淹没。

具体来说如果一块陆地像素与海洋相邻(上下左右四个相邻像素中有海洋)，它就会被淹没。

例如上图中的海域未来会变成如下样子：

.......
.......
.......
.......
....#..
.......
.......

请你计算：依照科学家的预测，照片中有多少岛屿会被完全淹没。

输入格式
第一行包含一个整数N。

以下 N 行 N 列，包含一个由字符”#”和”.”构成的 N×N 字符矩阵，代表一张海域照片，”#”表示陆地，”.”表示海洋。

照片保证第 1 行、第 1 列、第 N 行、第 N 列的像素都是海洋。

输出格式
一个整数表示答案。

数据范围

1≤N≤1000

输入样例1：

7
.......
.##....
.##....
....##.
..####.
...###.
.......

输出样例1：

1

输入样例2：

9
.........
.##.##...
.#####...
.##.##...
.........
.##.#....
.#.###...
.#..#....
.........

输出样例2：

1

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include

#define x first
#define y second

using namespace std;
typedef long long ll;
typedef pair<int, int> PII;
const int N = 1010;
const int MOD = 1000000007;
const int INF = 0x3f3f3f3f;

int gcd(int a, int b){return b ? gcd(b, a % b) : a;}

int n;
char g[N][N];
bool st[N][N];

int dx[] = {1, 0, -1, 0};
int dy[] = {0, 1, 0, -1};

void bfs(int sx, int sy, int &total, int &bound) {
	queue<PII> q;
	q.push({sx, sy});
	st[sx][sy] = true;
	while(!q.empty()) {
		PII t = q.front();
		q.pop();
		total ++ ;
		bool is_bound = false;
		for(int i = 0; i < 4; i ++ ) {
			int x = t.first + dx[i];
			int y = t.second + dy[i];
			if(x < 0 || y < 0 || x >= n || y >= n) continue;
			if(st[x][y]) continue;
			if(g[x][y] == '.') {
				is_bound = true;
				continue;
			}
			q.push({x, y});
			st[x][y] = true;
		}
		if(is_bound) bound ++ ;
	}
}

int main()
{	
	cin >> n;
	for(int i = 0; i < n; i ++ ) {
		for(int j = 0; j < n; j ++ ) {
			cin >> g[i][j];
		}
	}
	int cnt = 0;
	for(int i = 0; i < n; i ++ ) {
		for(int j = 0; j < n; j ++ ) {
			if(!st[i][j] && g[i][j] == '#') {
				int total = 0, bound = 0;
				bfs(i, j, total, bound);
				if(total == bound) cnt ++ ;
			}
		}
	}
	cout << cnt << endl;
	
	return 0;
}

1207. 大臣的旅费

很久以前，T王国空前繁荣。

为了更好地管理国家，王国修建了大量的快速路，用于连接首都和王国内的各大城市。

为节省经费，T国的大臣们经过思考，制定了一套优秀的修建方案，使得任何一个大城市都能从首都直接或者通过其他大城市间接到达。

同时，如果不重复经过大城市，从首都到达每个大城市的方案都是唯一的。

J是T国重要大臣，他巡查于各大城市之间，体察民情。

所以，从一个城市马不停蹄地到另一个城市成了J最常做的事情。

他有一个钱袋，用于存放往来城市间的路费。

聪明的J发现，如果不在某个城市停下来修整，在连续行进过程中，他所花的路费与他已走过的距离有关，在走第x千米到第x+1千米这一千米中（x是整数），他花费的路费是x+10这么多。也就是说走1千米花费11，走2千米要花费23。

J大臣想知道：他从某一个城市出发，中间不休息，到达另一个城市，所有可能花费的路费中最多是多少呢？

输入格式
输入的第一行包含一个整数 n，表示包括首都在内的T王国的城市数。

城市从 1 开始依次编号，1 号城市为首都。

接下来 n−1 行，描述T国的高速路（T国的高速路一定是 n−1 条）。

每行三个整数 Pi,Qi,Di，表示城市 Pi 和城市 Qi 之间有一条双向高速路，长度为 Di 千米。

输出格式
输出一个整数，表示大臣J最多花费的路费是多少。

数据范围

1≤n≤105 ,
1≤Pi,Qi≤n ,
1≤Di≤1000

输入样例：

5 
1  2  2 
1  3  1 
2  4  5 
2  5  4 

输出样例：

135

解题思路
由于题目说到不重复经过大城市，从首都到达每个大城市的方案都是唯一的。因此可以知道该图是一棵树，本题求的是树的直径

树的直径：树中长度最长的路径

1、任取一点x

2、找到距离x最远的点y

3、从y开始遍历，找到离y最远的点，与y最远的点的距离是树的直径

证明：AcWing 1207. 大臣的旅费

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include

#define x first
#define y second

using namespace std;
typedef long long ll;
typedef pair<int, int> PII;
const int N = 100010;
const int MOD = 1000000007;
const int INF = 0x3f3f3f3f;

int gcd(int a, int b){return b ? gcd(b, a % b) : a;}

int n;
struct Edge{
	int id, w;
};
vector<Edge> h[N];
int dist[N];

void dfs(int u, int father, int distance) {
	dist[u] = distance;
	for(int i = 0; i < h[u].size(); i ++ ) {
		if(h[u][i].id != father) {
			dfs(h[u][i].id, u, distance + h[u][i].w);
		}
	}
}

int main()
{	
	cin >> n;
	for(int i = 0; i < n; i ++ ) {
		int p, q, d;
		cin >> p >> q >> d;
		h[p].push_back({q, d});
		h[q].push_back({p, d});
	}
	int u = 1;
	dfs(u, -1, 0);
	for(int i = 1; i <= n; i ++ ) {
		if(dist[i] > dist[u]) {
			u = i;
		}
	}
	dfs(u, -1, 0);
	for(int i = 1; i <= n; i ++ ) {
		if(dist[i] > dist[u]) {
			u = i;
		}
	}
	int ans = dist[u];
	cout << ans * 10 + ans * (ans + 1ll) / 2 << endl;
	
	return 0;
}

826. 单链表

实现一个单链表，链表初始为空，支持三种操作：

向链表头插入一个数；
删除第 k 个插入的数后面的数；
在第 k 个插入的数后插入一个数。
现在要对该链表进行 M 次操作，进行完所有操作后，从头到尾输出整个链表。

注意:题目中第 k 个插入的数并不是指当前链表的第 k 个数。例如操作过程中一共插入了 n 个数，则按照插入的时间顺序，这 n 个数依次为：第 1 个插入的数，第 2 个插入的数，…第 n 个插入的数。

输入格式
第一行包含整数 M，表示操作次数。

接下来 M 行，每行包含一个操作命令，操作命令可能为以下几种：

H x，表示向链表头插入一个数 x。
D k，表示删除第 k 个插入的数后面的数（当 k 为 0 时，表示删除头结点）。
I k x，表示在第 k 个插入的数后面插入一个数 x（此操作中 k 均大于 0）。
输出格式
共一行，将整个链表从头到尾输出。

数据范围

1≤M≤100000

所有操作保证合法。

输入样例：

10
H 9
I 1 1
D 1
D 0
H 6
I 3 6
I 4 5
I 4 5
I 3 4
D 6

输出样例：

6 4 6 5

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include

#define x first
#define y second

using namespace std;
typedef long long ll;
typedef pair<int, int> PII;
const int N = 100010;
const int MOD = 1000000007;
const int INF = 0x3f3f3f3f;

int gcd(int a, int b){return b ? gcd(b, a % b) : a;}

int m;
int head, e[N], ne[N], idx;

void init() {
	head = -1;
	idx = 0;
}

void add_head(int x) {
	e[idx] = x;
	ne[idx] = head;
	head = idx;
	idx ++ ;
}

void add_k(int k, int x) {
	e[idx] = x;
	ne[idx] = ne[k];
	ne[k] = idx;
	idx ++ ;
}

void remove(int k) {
	ne[k] = ne[ne[k]];
}

int main()
{	
	init();
	cin >> m;
	while(m -- ) {
		char op;
		cin >> op;
		if(op == 'H') {
			int x;
			cin >> x;
			add_head(x);
		}
		else if(op == 'D') {
			int k;
			cin >> k;
			if(!k) head = ne[head];
			else remove(k - 1);
		}
		else if(op == 'I') {
			int k, x;
			cin >> k >> x;
			add_k(k - 1, x);
		}
	}
	for(int i = head; i != -1; i = ne[i] ) cout << e[i] << ' ';
	cout << endl; 
	
	return 0;
}