C语言实现离散余弦变换(DCT)并用MATLAB和Python验证

概念

离散余弦变换（Discrete Cosine Transform，DCT）是可分离的变换，其变换核为余弦函数。是与傅里叶变换相关的一种变换，它相当于把离散傅里叶变换的虚数部分丢掉，只使用实数。DCT除了具有一般的正交变换性质外， 它的变换阵的基向量能很好地描述人类语音信号和图像信号的相关特征。因此，在对语音信号、图像信号的变换中，DCT变换被认为是一种准最佳变换。
设x(n)是N个有限值的一维实数信号序列，$n=0,1,\cdots ,N-1$的完备正交归一函数如下：
$$\begin{array}{rl}X(k)& =a(k)\sum _{n=0}^{N-1}x(n)\cos \left[\frac{\pi (2n+1)k}{2N}\right]\\ x(n)& =a(k)\sum _{k=0}^{N-1}X(k)\cos \left[\frac{\pi (2n+1)k}{2N}\right]\end{array}$$
其中$a(k)$定义为：
$$a(k)=\{\begin{array}{ll}\sqrt{1/N}& k=0\\ \sqrt{2/N}& 1\le k\le N-1\end{array}$$
由上述两个式子可以得到DCT的另一种表现形式：
$$X(k)=\sqrt{\frac{2}{N}}\sum _{n=0}^{N}C(k)x(n)\cos \left[\frac{\pi (2\pi +1)k}{2N}\right]k=0,1\dots ,N-1$$

任务需求

我们产生一个幅度为1，频率为100hz，采样频率为5000的正弦波信号，并对其进行DFC变换，将产生的正弦波信号保存在text.txt中，将经过DCT变换的数据保存在result.txt文件中。再把text.txt数据放到MATLAB和Python中验证,检验数据计算是否正确。

C语言实现

在C语言环境下的代码如下：

#include 
#include 
#include
#define PI 3.1415926
void main(int argc,char* argv[])
{
	double A = atof(argv[1]);//幅度
	double f = atof(argv[2]);//频率/hz
	double fn = atof(argv[3]);//采样频率
	int len = (int)fn;//ken就是长度N
	double x[len];
	double X[len];
	double t,data;
	int i,j,k;
	double ak;
	FILE* fp1 = fopen("test.txt","w");
	FILE* fp2 = fopen("result.txt","w");
    for (i = 0; i < len; i++)
    {//产生信号
        t = i / fn;
        x[i] = A * sin(2 * PI * f * t);
		//printf("%d %lf\n", i, x[i]);
		fprintf(fp1, "%lf\n", x[i]);
    }
	//DFT变换
	//求出a(k)
	for(k=0;k<len;k++)
	{
		double data =0;
		if(k==0)         //计算k=0时的ak
		ak=sqrt(1.0/len);  
		else           //计算k!=0时的ak
		ak=sqrt(2.0/len);
		for(j=0;j<len;j++)//离散余弦变换 
		{
			t = x[j]*cos(((2*j+1)*k*PI)/(2*len));
			data = data + t;    //累加求和
		}
		X[k]=ak*data;//X[k]等于累和结果s乘以系数C
	}
	for(k=0;k<len;k++)  
	{
       //printf("%dDFC:%lf\n",k,X[k]);
	   fprintf(fp2, "%.4f\n", X[k]);//输出离散余弦变换结果 
	}
	printf("successfully!");
}

在cmd中输入如下指令进行编译和运行

gcc dct-c.c
a.exe 1 100 5000

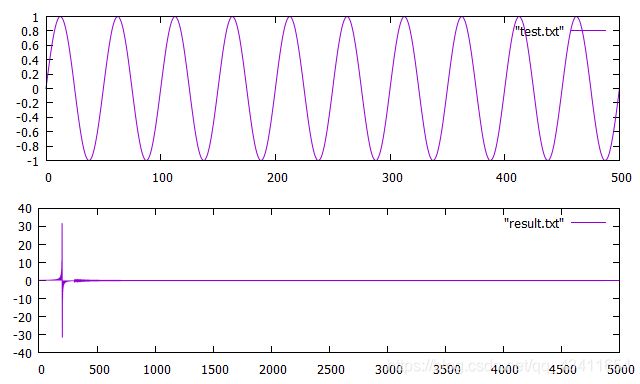
打开test.txt和result.txt文件，查看输出的数据是否是5000行，输出结果如下。

在gnuplot中输入如下的代码绘制出图像

set multiplot layout 2,1
set xrange[0:500]
plot "test.txt" w l
unset xrange
plot "result.txt" w l

MATLAB验证

在MATLAB环境下的代码如下：

close all;
x=load("test.txt");%加载数据
subplot(211);%两个子图
plot(x)%绘制原始的信号图
xlim([0,500]);%控制x轴范围
y=dct(x);%进行dct变换
subplot(212);%第二个子图
plot(y);%绘制变换后的频谱图

MATLAB中的输出结果

Python实现

在Python环境下的代码如下：

import numpy as np
from scipy.fftpack import dct
import matplotlib.pyplot as plt
file = 'test.txt'
data = np.loadtxt(file)#读入数据
a = len(data)#计算数据长度
x1 = np.linspace(0, 1, a)#创建0-1的等差数组 a个
y = dct(data)#对数据进行dct变换
plt.subplot(211)#绘制第一幅图
plt.xlim((0, 0.1))#控制xy轴范围
plt.ylim((-2, 2))#图表标题
plt.title('signal', fontsize=12, color='black')
plt.plot(x1,data)

plt.subplot(212)#绘制第二幅图
plt.title('dct', fontsize=12, color='black')
plt.plot(y)#控制两幅子图的上下间距
plt.subplots_adjust(left=None, bottom=None, right=None, top=None,wspace=None, hspace=1)
plt.savefig('1.7.eps')#保存为eps矢量图
plt.show()

在Python中的输出结果如图
可以验证我们C语言实现的算法是正确的。