【LeetCode】《LeetCode 101》第五章:排序算法
文章目录
- 5.1 常用的排序算法
-
- 1. 快速排序
- 2. 归并排序
- 3. 插入排序
- 4. 冒泡排序
- 5. 选择排序
- 6. 总结
- 5.2 快速选择
-
- 215. 数组中的第K个最大元素(中等)
- 5.3 桶排序
-
- 347. 前 K 个高频元素(中等)
- 5.4 练习
-
- 451. 根据字符出现频率排序(中等)
- 75. 颜色分类(中等)
- 5.5 总结
5.1 常用的排序算法
以下代码均采用 左闭右开 的写法。
1. 快速排序
快速排序是从冒泡排序演变而来的算法,但是比冒泡排序要高效得多,所以叫做快速排序。快速排序之所以快速,是因为它使用了“分治法”。
快速排序也属于交换排序,通过元素之间的比较和交换位置来达到排序的目的。
快速排序在每一轮挑选一个基准元素,并让其他比它大的元素移动到数列一边,比它小的元素移动到数列的另一边,从而把数列拆解成了两个部分。
void quick_sort(vector<int> &nums, int l, int r){
if(l + 1 >= r){
return ;
}
int first = l, last = r - 1, key = nums[first];
while(first < last){
while(first < last && nums[last] >= key){
-- last;
}
nums[first] = nums[last];
while(first < last && nums[first] <= key){
++ first;
}
nums[last] = nums[first];
}
nums[first] = key;
quick_sort(nums, l, first);
quick_sort(nums, first + 1, r);
}
2. 归并排序
归并排序图文详解
归并排序结合了递归的思想和有序数组合并的算法。
将整个数组进行不断划分,直到划分的每个字数组的长度为0或者为1,这时每个字数组都是有序数组,再按照有序数组的拼接算法,对每个子数组进行拼接,就能保证每次的拼接结果还是有序的。最终拼接成一个数组后,整个数组也是有序的,所以数组完成排序。关于子数组的划分,实际上是通过递归实现的。
时间复杂度低,但是空间复杂度很高。
void merge_sort(vector<int> &nums, int l, int r, vector<int> &temp){
// 直到每个子数组最多只有一个元素
if(l + 1 >= r) return ;
// divide
int m = l + (r - l) / 2;
// 左边子数组继续划分
merge_sort(nums, l, m, temp);
// 右边子数组继续划分
merge_sort(nums, m, r, temp);
// conquer
// 两个有序数组归并
// p 指向第一个数组 q 指向第二个数组
int p = l, q = m, i = l;
while(p < m || q < r){
// 如果第二个数组已经遍历结束
// 或 第一个数组当前指向的值小于等于第二个数组
// 选择第一个数组的元素放入临时数组 temp
if(q >= r || (p < m && nums[p] <= nums[q])){
temp[i++] = nums[p++];
}
// 否则选择第二个数组的值放入临时数组 temp
else{
temp[i++] = nums[q++];
}
}
// 最后需要把临时数组的值放回原数组
for(i = l; i < r; ++i){
nums[i] = temp[i];
}
}
3. 插入排序
通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
插入排序在实现上,需要用到O(1)的额外空间的排序,因而在从后向前扫描过程中,需要反复把已排序元素逐步向后挪位,为最新元素提供插入空间。
void insertion_sort(vector<int> &nums, int n){
for(int i = 0; i < n; ++i){
for(int j = i; j > 0 && nums[j] < nums[j-1]; --j){
swap(nums[j], nums[j-1]);
}
}
}
4. 冒泡排序
依次比较两个相邻的子元素,如果他们的顺序错误就把他们交换过来,重复地进行此过程直到没有相邻元素需要交换,即完成整个冒泡。
每一趟只能确定将一个数归位。即第一趟只能确定将末位上的数归位,第二趟只能将倒数第2位上的数归位,依次类推下去。如果有n个数进行排序,只需将n-1个数归位,也就是要进行n-1趟操作。
而"每一趟”都需要从第一位开始进行相邻的两个数的比较,将较大的数放后面,比较完毕之后向后挪一位继续比较下面两个相邻的两个数大小关系,重复此步骤,直到最后一个还没归位的数。
void bubble_sort(vector<int> &nums, int n){
bool swapped;
for(int i = 1; i < n; ++i){
swapped = false;
for(int j = 1; j < n - i + 1; ++j){
if(nums[j] < nums[j-1]){
swap(nums[j], nums[j-1]);
swapped = true;
}
}
if(!swapped) break;
}
}
5. 选择排序
选择排序思想
选择排序又称简单选择排序,是一种不稳定的排序方法,其基本思想是:第 i 趟排序在待排序序列 a[i]~a[n] 中选取关键码最小的记录,并和第 i 个记录交换作为有序序列的第 i 个记录。
其实现利用双重循环,外层 i 控制当前序列最小值存放的数组元素位置,内层循环 j 控制从 i+1 到 n 序列中选择最小的元素所在位置 k 。
void selection_sort(vector<int> &nums, int n){
int mid;
for(int i = 0; i < n - 1; ++i){
mid = i; // mid 保存无序区第一个值的下标
for(int j = i + 1; j < n ; ++j){
// 寻找无序区中最小的值的下标
if(nums[j] < nums[mid]){
mid = j;
}
}
// 将无序区中的最小值和无序区第一个值交换
// 此时有序区的元素个数有 i+1 个
swap(nums[mid], num[i]);
}
}
6. 总结
以上排序代码调用方法为:
void sort(){
vector<int> nums = {1, 3, 5, 7, 2, 6, 4, 8};
vector<int> temp(nums.size());
sort(nums.begin(), nums.end());
quick_sort(nums, 0, nums.size());
merge_sort(nums, 0, nums.size(), temp);
insertion_sort(nums, nums.size());
bubble_sort(nums, nums.size());
selection_sort(nums, nums.size());
}
5.2 快速选择
215. 数组中的第K个最大元素(中等)
-
思路
- 快速选择 一般用于求解 k-th Element 问题,可以在O(n)时间复杂度,O(1)空间复杂度完成求解工作。
- 快速选择的实现和快速排序类似,不过只需要找到第 k 大的枢(pivot) 即可,不需要对其左右进行排序。
- 与快速排序一样,快速选择需要先打乱数组,即随机化,随机挑选一个值作为枢 ,否则最坏情况下时间复杂度为O(n2)。
- 这一题需要找到第 k 个最大的元素,也就是降序排序后,返回 下标为 k-1 的元素。因此,在快速排序的时候,需要使用随机化降低时间复杂度。在第一次粗略排序后,nums[k-1] 一定在枢的左半边或右半边,此时只需要递归其中一半,可以大大减少时间复杂度。
-
代码
class Solution { public: int findKthLargest(vector<int>& nums, int k) { // 降序快排 quick_sort(nums, 0, nums.size(), k - 1); // 返回下标为 k-1 的元素 return nums[k-1]; } // 快速排序 // 使得左边的数都比key大 右边的数都比key小 void quick_sort(vector<int> &nums, int l, int r, int target){ if(l + 1 >= r) return ; int first = l, last = r - 1; // 采用随机化 避免极端情况 // 时间复杂度才能从 O(logn) -> O(n) srand(time(nullptr)); int random = rand() % (r - l) + l; // 将随机选取的key值放到数组的起始位置 swap(nums[random], nums[first]); int key = nums[first]; while(first < last){ // 移动last指针 保证key右边的数都小于它 while(first < last && nums[last] <= key){ last--; } swap(nums[first], nums[last]); // 移动first指针 保证key左边的数都大于它 while(first < last && nums[first] >= key){ first++; } swap(nums[last], nums[first]); } nums[last] = key; // 因为 nums[k-1] 只会在key的左边或右边 // 分类考虑可以大大降低时间复杂度 if(target <= first) quick_sort(nums, l, first, target); else quick_sort(nums, first + 1, r, target); } }; -
收获
- 这道题之前做过,那时候一知半解,现在大致了解了排序的思想后,比较容易理解这道题的思路。
- 总结:如果遇到求数组中第 k 大的元素,可以使用快排;如果时间复杂度限制在 O(n),加上随机化的思想和只递归其中一边的策略。
5.3 桶排序
347. 前 K 个高频元素(中等)
![]()
![]()
-
思路
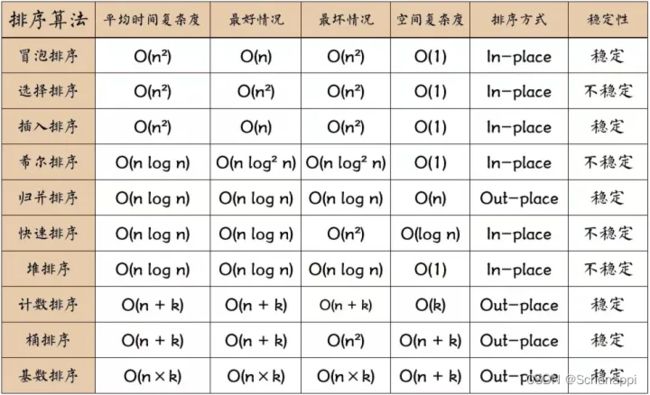
- 由于这道题需要保证时间复杂度优于 O(n log n),因此常规的排序算法都不满足要求,通过查看 5.1 的总结,发现桶排序的时间复杂度为 O(n + k) ,可以使用。
- 桶排序,就是为每个值设立一个桶,桶内记录这个值的出现次数(或者其他属性),然后对桶进行排序。
- 针对样例,我们先通过桶排序得到四个桶 [1,2,3,4],它们的值分别为[4,2,1,1],表示每个数字的出现次数。这里可以用
unordered_map实现。 - 接着,我们对桶的频次排序,前 k 个大桶是前 k 个频繁的数。在这里,我们可以再进行一次桶排序,把每个旧桶根据频次放在不同的新桶内。针对样例来说,因为目前最大频次是 4,我们建立 [1,2,3,4] 四个新桶,将它们分别放入的旧桶为 [[3,4],[2],[],[1]],表示不同数字的出现频率。这里可以用
二维数组实现,下标作为出现频率。 - 最后,从后往前遍历(因为频率越大,下标越大),直到找到 k 个旧桶。
- 针对样例,我们先通过桶排序得到四个桶 [1,2,3,4],它们的值分别为[4,2,1,1],表示每个数字的出现次数。这里可以用
-
代码
class Solution { public: vector<int> topKFrequent(vector<int>& nums, int k) { // 将元素存入计数桶 unordered_map<int, int> counts; int max_count = 0; // 记录最高频次 for(int n : nums){ max_count = max(max_count, ++counts[n]); } // 二维数组 频次作为下标 // 因此对数组buckets从后往前遍历,即从大到小遍历 vector<vector<int>> buckets(max_count + 1); for(auto count : counts){ buckets[count.second].push_back(count.first); } vector<int> ans; int cnt = 0; for(int i = max_count; i>=0 && ans.size() < k; --i){ for(int n : buckets[i]){ ans.push_back(n); if(ans.size() == k) break; } } return ans; } }; -
收获
- 学习了桶排序,基本都是看着题解写的。
5.4 练习
451. 根据字符出现频率排序(中等)
-
思路
- 这题是频率排序问题,因此使用桶排序。
- 首先统计字符串中字符的出现次数。为每个字符设立一个桶,桶里面存放该字符的出现次数;
- 接着,对桶里的出现次数使用桶排序。这里用了
unordered_map,映射字符出现次数和字符数组(该数组里存放出现次数相同的字符)。由于出现次数和下标相对应,所以此时字符的出现次数是升序的。 - 最后,从后往前遍历,按降序依次得到字符,并按照出现次数将字符添加到答案字符串中。
-
代码
class Solution { public: string frequencySort(string s) { unordered_map<char, int> counts; int max_count = 0; // 统计最大频次 for(char ch : s){ max_count = max(max_count, ++counts[ch]); } // 出现次数,字符数组(保存出现i次的字符) unordered_map<int, vector<char>> buckets; for(auto count : counts){ buckets[count.second].push_back(count.first); } string ans; for(int i = max_count; i > 0 ; --i){ for(char ch : buckets[i]){ // 该字符出现几次就要添加几次 for(int j=i; j>0; j--){ ans.push_back(ch); } } } return ans; } }; -
收获
- 刚学完桶排序,做这道题就很轻松。代码基本是上一道题一致,修改了对频率进行桶排序时使用的数据结构。
- 总结一下,以后遇到频率排序相关问题,应该先思考是否可以使用桶排序。
75. 颜色分类(中等)
-
题解
-
由于这道题要求仅使用常数空间,只能扫描一遍,此时已经排除了大部分常规的排序方法。因此,本题使用 快速排序 的子过程 partition:通过一次遍历,将数组分成三个部分。
-
写代码的时候需要注定到设置的变量以及区间的定义,也就是循环不变量。
所谓循环不变量就是在每次循环的时候,都满足的一个条件。
对于这道题,我们可以为 3 个值划分三个区间,分别为:0∈nums[0, p0),1∈nums[p0, i),2∈nums(p2, nums.size() - 1]。这三个区间就是这道题的循环不变量,每次循环的时候,每个值必须属于这个区间。
-
在设置完三个区间后,我们需要保证每个区间初始的时候都是空集,因此要严格设置
p0, i, p2的值。其中p0指向 0 的下一个元素,i指向当前遍历到的元素,p2指向 2 的前一个元素。 -
然后开始从左到右进行一次遍历,当
i > p2的时候,遍历结束。因为第二个区间和第三个区间的指针都是开区间,因此 当i == p2的时候,还需要进行一次判断。- 如果
nums[i] == 0,那么就swap(nums[i], nums[p0]);,同时 指针p0和i向前移动一位,前者是保证p0指向的元素为 0 的下一个元素,后者是继续遍历下一个元素。 - 如果
nums[i] == 1,此时不需要改变p0和p2,因此只需要移动i,遍历下一个元素; - 如果
nums[i] == 2,那么就swap(nums[i], nums[p2]);,同时p2--,保证p2指向的元素为 2 的前一个元素;此时不需要移动i,因为两个元素交换之后,指针i指向的值还没有判断。
- 如果
-
-
代码
class Solution { public: void sortColors(vector<int>& nums) { // 定义循环不变量 // nums[0, p0) = 0; // nums[p0, i) = 1; // nums(p2, len-1] = 2; // 一开始需要让三个区间都为空区间 int p0 = 0, i = 0, p2 = nums.size() - 1; while(i <= p2){ // 因为 i == p2 这个点不包含在区间内 // 所以需要判断 if(nums[i] == 0){ swap(nums[i], nums[p0]); p0 ++; i ++; }else if(nums[i] == 1){ i++; }else if(nums[i] == 2){ swap(nums[i], nums[p2]); p2 --; // 这里没有i++ 是因为: // 原先下标p2的值移动到i,这个值还没有判断 } } } }; -
收获
- 一开始没看清题目要求一次遍历,直接用了冒泡排序,还想着这题这么简单。看了题解之后学了循环不变量,是以前没接触过的知识点。
5.5 总结
- 排序算法很多,也比较容易记混,感觉日后要多做题记住各个排序的特点及模板。