IEArch-矩阵乘法模块
一、思考题
回答 4.1.5 疑问中的疑问,
问题 1 —— 第二个矩阵计算为何出错,
问题 2 —— MAC.v 是否有修改的必要
1.1 问题 1
第一个矩阵出错的原因是在第二个矩阵计算中,在第一个矩阵中涉及到了负数
[[ 111, 25, 32, 66, -12, -99, -28, 16, -95],
[ 63, -90, -102, 40, 73, 16, -53, -33, -27],
[ -39, -79, -12, -83, -112, 59, 34, -49, -57],
[ -18, 103, -86, -51, -104, 36, -105, 112, 58],
[ 52, -12, -52, 1, -95, -123, 34, -89, 11],
[ 50, 123, 90, -74, 99, 100, 95, -12, -97],
[ 12, -94, 55, -14, 115, 84, -110, 64, 18],
[ 74, -105, -111, -43, 63, 107, 111, 56, -15]]
而在 MAC.v 代码中,对于乘法的计算,是这样的
wire signed [15:0] sf_data;
assign sf_data = $signed({8'b0, f_data});
// 本级计算
reg signed [31:0] data_reg; // 存储乘累加的结果
always @(posedge clk or posedge rst) begin
// 复位清零
if (rst) begin
data_reg <= 32'b0;
end
// 如果 valid
else if (valid) begin
// 到了最后一次计算的时候,就交给输出计算,自己复位
if (last) begin
data_reg <= 32'b0;
end
// 进行一个乘累加操作
else begin
data_reg <= data_reg + $signed(w_data) * $signed(sf_data);
end
end
// 保持原值不变
else begin
data_reg <= data_reg;
end
end
因为 8 位的操作数乘法运算,可能出现 16 位的结果,而零拓展只适用于无符号乘法,而第二个矩阵中出现的第一个矩阵中出现了负数,这就导致了运算错误的出现。只需要将其修改如下
assign sf_data = $signed( {{8{f_data[7]}}, f_data}); // 修改后
assign sf_data = $signed({8'b0, f_data}); // 修改前
那么就可以有 test.py 中的输出结果,如图所示
1.1 问题 2
没有必要修改,因为根据题义描述,这个模块将被用于全连接层,其输入格式是
feature 是 uint8,weight 是 int8
全连接层的计算方式为 F ⋅ W F \cdot W F⋅W 。从上面的分析可以看出,这个模块未修改前对于 W W W 中的负数分量就可以正确处理,只是没有办法处理 F F F 中的负数分量,但是由输入格式可知, F F F 的分量是 uint8,其范围是 0 ~ 255 所以不会出现负数情况,所以是没有必要修改的。
二、矩阵乘模块设计文档
2.1 设计功能
对于 Multiply_8x8 模块,它接受一个 8 x num 的分量为 uint8 的 F e a t u r e Feature Feature 矩阵和一个 num x 8 的分量为 int 的 W e i g h t Weight Weight 矩阵,在经过一定的周期后输出 F e a t u r e ⋅ W e i g h t Feature \cdot Weight Feature⋅Weight 。
对于 MAC 模块,它将输入的 uint8 的值和 int8 的值相乘,并与保存在寄存器中的值进行加和,然后将结果继续保存在这个寄存器中。除了计算功能以外,MAC 还有传递输入数据和传递计算结果的功能。
2.2 接口说明
对于 Multiply_8x8 模块有
| 名称 | 位宽 | 符号 | 方向 | 含义 |
|---|---|---|---|---|
| clk | 1 | unsigned | input | 时钟信号 |
| rst | 1 | unsigned | input | 复位信号 |
| fvalid0 | 1 | unsigned | input | F F F 矩阵的第 0 行输入是否有效 |
| fdata0 | 8 | unsigned | input | F F F 矩阵的第 0 行输入数据 |
| fvalid1 | 1 | unsigned | input | F F F 矩阵的第 1 行输入是否有效 |
| fdata1 | 8 | unsigned | input | F F F 矩阵的第 1 行输入数据 |
| fvalid2 | 1 | unsigned | input | F F F 矩阵的第 2 行输入是否有效 |
| fdata2 | 8 | unsigned | input | F F F 矩阵的第 2 行输入数据 |
| fvalid3 | 1 | unsigned | input | F F F 矩阵的第 3 行输入是否有效 |
| fdata3 | 8 | unsigned | input | F F F 矩阵的第 3 行输入数据 |
| fvalid4 | 1 | unsigned | input | F F F 矩阵的第 4 行输入是否有效 |
| fdata4 | 8 | unsigned | input | F F F 矩阵的第 4 行输入数据 |
| fvalid5 | 1 | unsigned | input | F F F 矩阵的第 5 行输入是否有效 |
| fdata5 | 8 | unsigned | input | F F F 矩阵的第 5 行输入数据 |
| fvalid6 | 1 | unsigned | input | F F F 矩阵的第 6 行输入是否有效 |
| fdata6 | 8 | unsigned | input | F F F 矩阵的第 6 行输入数据 |
| fvalid7 | 1 | unsigned | input | F F F 矩阵的第 7 行输入是否有效 |
| fdata7 | 8 | unsigned | input | F F F 矩阵的第 7 行输入数据 |
| wvalid0 | 1 | unsigned | input | W W W 矩阵的第 0 列输入是否有效 |
| wdata0 | 8 | signed | input | W W W 矩阵的第 0 列输入数据 |
| wvalid1 | 1 | unsigned | input | W W W 矩阵的第 1 列输入是否有效 |
| wdata1 | 8 | signed | input | W W W 矩阵的第 1 列输入数据 |
| wvalid2 | 1 | unsigned | input | W W W 矩阵的第 2 列输入是否有效 |
| wdata2 | 8 | signed | input | W W W 矩阵的第 2 列输入数据 |
| wvalid3 | 1 | unsigned | input | W W W 矩阵的第 3 列输入是否有效 |
| wdata3 | 8 | signed | input | W W W 矩阵的第 3 列输入数据 |
| wvalid4 | 1 | unsigned | input | W W W 矩阵的第 4 列输入是否有效 |
| wdata4 | 8 | signed | input | W W W 矩阵的第 4 列输入数据 |
| wvalid5 | 1 | unsigned | input | W W W 矩阵的第 5 列输入是否有效 |
| wdata5 | 8 | signed | input | W W W 矩阵的第 5 列输入数据 |
| wvalid6 | 1 | unsigned | input | W W W 矩阵的第 6 列输入是否有效 |
| wdata6 | 8 | signed | input | W W W 矩阵的第 6 列输入数据 |
| wvalid7 | 1 | unsigned | input | W W W 矩阵的第 7 列输入是否有效 |
| wdata7 | 8 | signed | input | W W W 矩阵的第 7 列输入数据 |
| num_valid_ori | 1 | unsigned | input | W W W 矩阵的列数(同时也是 F F F 的行数)是否有效 |
| num_ori | 32 | unsigned | input | W W W 矩阵的列数(同时也是 F F F 的行数) |
| valid_o0 | 1 | unsigned | output | 结果矩阵的第 0 行是否有效 |
| data_o0 | 32 | signed | output | 结果矩阵的第 0 行输出数据 |
| valid_o1 | 1 | unsigned | output | 结果矩阵的第 1 行是否有效 |
| data_o1 | 32 | signed | output | 结果矩阵的第 1 行输出数据 |
| valid_o2 | 1 | unsigned | output | 结果矩阵的第 2 行是否有效 |
| data_o2 | 32 | signed | output | 结果矩阵的第 2 行输出数据 |
| valid_o3 | 1 | unsigned | output | 结果矩阵的第 3 行是否有效 |
| data_o3 | 32 | signed | output | 结果矩阵的第 3 行输出数据 |
| valid_o4 | 1 | unsigned | output | 结果矩阵的第 4 行是否有效 |
| data_o4 | 32 | signed | output | 结果矩阵的第 4 行输出数据 |
| valid_o5 | 1 | unsigned | output | 结果矩阵的第 5 行是否有效 |
| data_o5 | 32 | signed | output | 结果矩阵的第 5 行输出数据 |
| valid_o6 | 1 | unsigned | output | 结果矩阵的第 6 行是否有效 |
| data_o6 | 32 | signed | output | 结果矩阵的第 6 行输出数据 |
| valid_o7 | 1 | unsigned | output | 结果矩阵的第 7 行是否有效 |
| data_o7 | 32 | signed | output | 结果矩阵的第 7 行输出数据 |
对于 MAC 模块,有
| 名称 | 位宽 | 符号 | 方向 | 含义 |
|---|---|---|---|---|
| clk | 1 | unsigned | input | 时钟信号 |
| rst | 1 | unsigned | input | 复位信号 |
| num_valid | 1 | unsigned | input | 乘累加长度 num 是否有效 |
| num | 32 | unsigned | input | 乘累加长度 |
| num_r_valid | 1 | unsigned | output | 传播到下一 MAC 的乘累加长度是否有效 |
| num_r | 32 | unsigned | output | 传播到下一 MAC 的乘累加长度 |
| w_valid | 1 | unsigned | input | W W W 矩阵的一个分量是否有效 |
| w | 8 | signed | input | W W W 矩阵的一个分量 |
| w_r_valid | 1 | unsigned | output | 传播到下一 MAC 的 W W W 矩阵的一个分量是否有效 |
| w_r | 8 | signed | output | 传播到下一 MAC 的 W W W 矩阵的一个分量长度 |
| f_valid | 1 | unsigned | input | F F F 矩阵的一个分量是否有效 |
| f | 8 | unsigned | input | F F F 矩阵的一个分量 |
| f_r_valid | 1 | unsigned | output | 传播到下一 MAC 的 F F F 矩阵的一个分量是否有效 |
| f_r | 8 | unsigned | output | 传播到下一 MAC 的 F F F 矩阵的一个分量长度 |
| valid_l | 1 | unsigned | input | 下一个 MAC 的运算结果是否有效 |
| data_l | 32 | signed | input | 下一个 MAC 的运算结果 |
| valid_o | 1 | unsigned | output | 该 MAC 的运算结果是否有效 |
| data_o | 32 | signed | output | 该 MAC 的运算结果 |
2.3 设计思想及流程描述
为了更好的展示设计思想和流程,这里采用一个简化版的矩阵乘法,比较方便描述。
流程主要分为两个部分,一个是计算,一个是将结果传出。
2.3.1 简单流程模拟
我们规定我们的需求是计算
F 2 × 3 ⋅ W 3 × 2 = R 2 × 2 F_{2 \times 3} \cdot W_{3 \times 2} = R_{2\times 2} F2×3⋅W3×2=R2×2
其中有
F = [ 1 2 3 4 5 6 ] W = [ 7 8 9 10 11 12 ] F = \left[ \begin{matrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{matrix} \right] \quad\quad W = \left[ \begin{matrix} 7 & 8 \\ 9 & 10\\ 11 & 12 \end{matrix} \right] F=[142536]W= 791181012
此时我们只需要一个 2 x 2 个 MAC 即可完成运算,如下所示
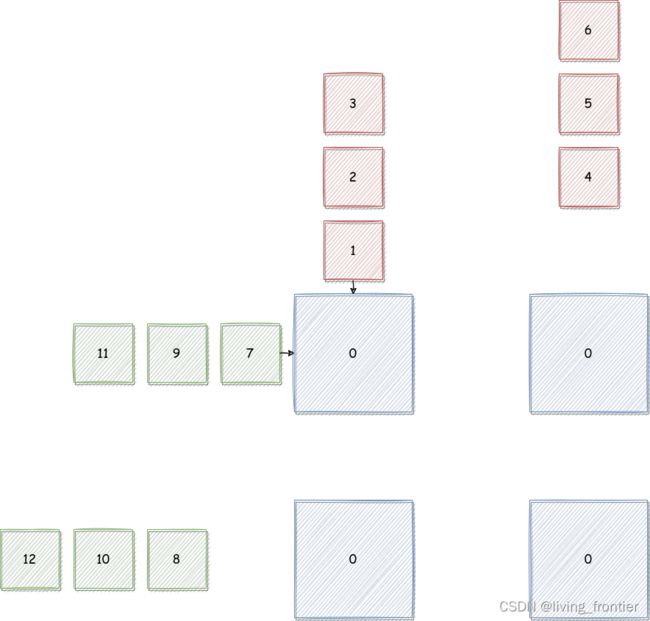
Cycle 0
首先数据呈现这这种形式
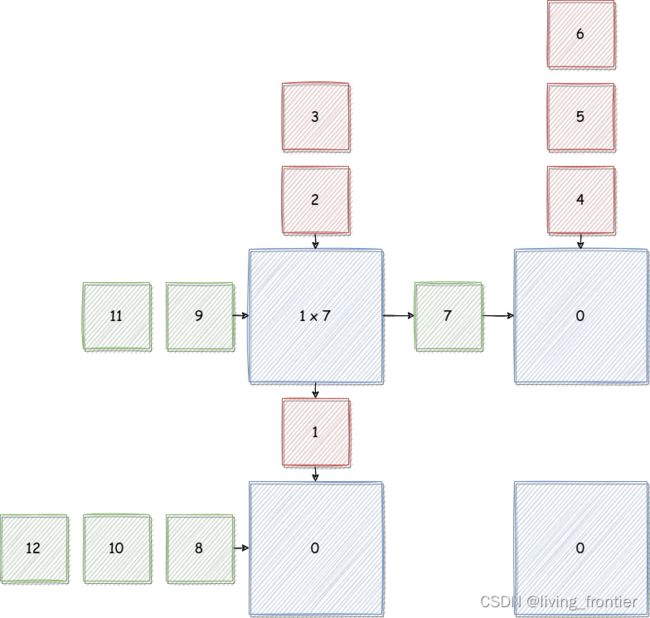
Cycle 1
Cycle 2
Cycle 3
Cycle 4
Cycle 5
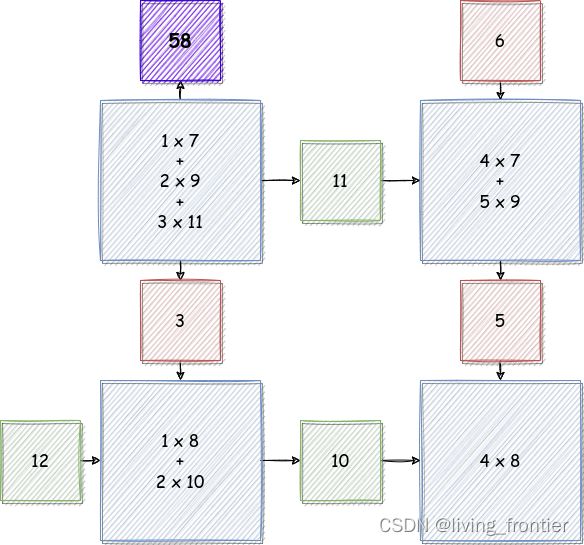
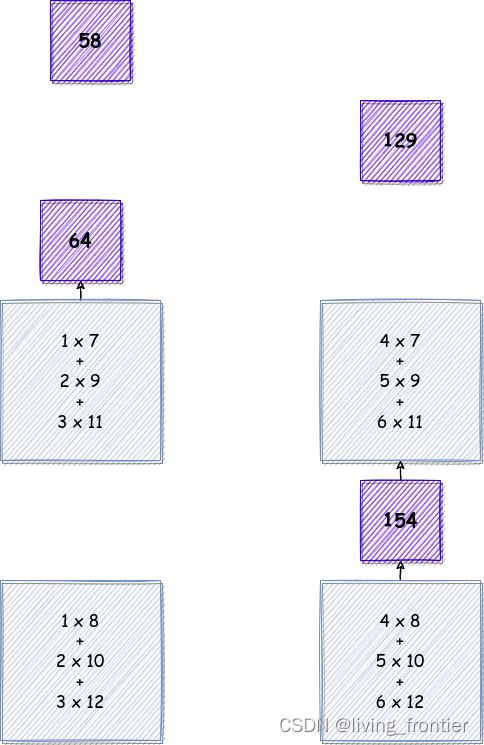
Cycle 6
对于这样的一个计算,需要花
2 + 3 + 2 = 7 2 + 3 + 2 = 7 2+3+2=7
个周期就可以得到结果。
2.3.2 设计思想
对于矩阵乘法,可以看做是一堆数进行有规律、有复用的乘加运算,所以搭建模块解决这个问题,需要将其按照规律一步一步的进行计算。普世分析
A p × n ⋅ B n × q = R p × q A_{p \times n} \cdot B_{n \times q} = R_{p \times q} Ap×n⋅Bn×q=Rp×q
对于 MAC 模块,它对应这结果矩阵 R R R 中的一个分量,为了计算这个分量,需要进行 n 次的乘并累加操作。所以一般是在 n 个周期内完成的。需要注意的是,对于 A , B A, B A,B 中的某个分量,不止会被一个 MAC 利用,所以 MAC 还承担着传播分量的作用,除此之外,MAC 计算出结果后,还需要将结果通过 MAC 网络传递出去。
那么又没有什么更快的改进方法呢,其实是有的,比如说下面这种方法,就可以缩短传入的时间
但是要付出更多的布线还有驱动的代价,所以综合考虑,还是利用了第一种。
2.4 内部关键信号与变量描述
在 MAC 中,固定长度的累加操作,是通过一个计数器 num_cnt 实现的,如下所示
// 本级控制信号
reg [31:0] num_cnt; // 已经计算的轮数
wire valid = w_valid & f_valid; // 输入数据是否有效
wire last = (num_cnt == num_r - 1'b1); // 是否是最后一次计算
// num_cnt 用于计数
always @(posedge clk or posedge rst) begin
// 复位
if (rst) begin
num_cnt <= 32'b0;
end
// 当 valid 信号有效时,num_cnt 会发生变化
else if (valid) begin
// 应该是 cnt 增加到一定的值(num_r)以后,就会重新开始
if (last) begin
num_cnt <= 32'b0;
end
// num_cnt 递增
else begin
num_cnt <= num_cnt + 1'b1;
end
end
// valid 信号无效,则保持原值
else begin
num_cnt <= num_cnt;
end
end
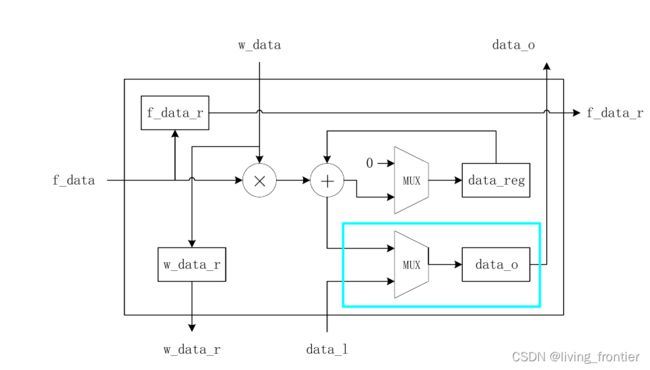
MAC 不仅需要传输自己的运算结果,而且需要传输其下面的 MAC 传输的结果,是通过一个 MUX 实现的,如下所示
这个结构的对应代码如下
// 数据输出,纵向向上传播
always @(posedge clk or posedge rst) begin
if (rst) begin
data_o <= 32'b0;
end
// 最后一次的计算在这里进行
else if (valid & last) begin
data_o <= data_reg + $signed(w_data) * $signed(sf_data);
end
// 数据被更新成一个外来值
else if (valid_l) begin
data_o <= data_l;
end
// 保持原值
else begin
data_o <= data_o;
end
end
// valid_o 是一个输出项,当 data_o 有效的时候,他就是有效的
always @(posedge clk or posedge rst) begin
if (rst) begin
valid_o <= 32'b0;
end
else begin
valid_o <= (valid & last) | valid_l;
end
end
可以看到当输出数据有两个来源,一个是本身计算的数据 data_reg 一个是其下的 MAC 的计算数据 data_l 。而且 data_l 的优先级更高,这是因为当下方数据有效时,当前 MAC 一定已经计算出来了。
在 Multiply_8x8 中,这个模块控制了数据的流向,比如说纵向传播,写法是这样的
assign w_valid[0] = wvalid0;
assign w_valid[1] = wvalid1;
assign w_valid[2] = wvalid2;
assign w_valid[3] = wvalid3;
assign w_valid[4] = wvalid4;
assign w_valid[5] = wvalid5;
assign w_valid[6] = wvalid6;
assign w_valid[7] = wvalid7;
assign w_valid[8] = w_valid_r[0];
assign w_valid[9] = w_valid_r[1];
assign w_valid[10] = w_valid_r[2];
assign w_valid[11] = w_valid_r[3];
assign w_valid[12] = w_valid_r[4];
assign w_valid[13] = w_valid_r[5];
assign w_valid[14] = w_valid_r[6];
assign w_valid[15] = w_valid_r[7];
assign w_valid[16] = w_valid_r[8];
assign w_valid[17] = w_valid_r[9];
assign w_valid[18] = w_valid_r[10];
assign w_valid[19] = w_valid_r[11];
assign w_valid[20] = w_valid_r[12];
assign w_valid[21] = w_valid_r[13];
assign w_valid[22] = w_valid_r[14];
assign w_valid[23] = w_valid_r[15];
assign w_valid[24] = w_valid_r[16];
assign w_valid[25] = w_valid_r[17];
assign w_valid[26] = w_valid_r[18];
assign w_valid[27] = w_valid_r[19];
assign w_valid[28] = w_valid_r[20];
assign w_valid[29] = w_valid_r[21];
assign w_valid[30] = w_valid_r[22];
assign w_valid[31] = w_valid_r[23];
assign w_valid[32] = w_valid_r[24];
assign w_valid[33] = w_valid_r[25];
assign w_valid[34] = w_valid_r[26];
assign w_valid[35] = w_valid_r[27];
assign w_valid[36] = w_valid_r[28];
assign w_valid[37] = w_valid_r[29];
assign w_valid[38] = w_valid_r[30];
assign w_valid[39] = w_valid_r[31];
assign w_valid[40] = w_valid_r[32];
assign w_valid[41] = w_valid_r[33];
assign w_valid[42] = w_valid_r[34];
assign w_valid[43] = w_valid_r[35];
assign w_valid[44] = w_valid_r[36];
assign w_valid[45] = w_valid_r[37];
assign w_valid[46] = w_valid_r[38];
assign w_valid[47] = w_valid_r[39];
assign w_valid[48] = w_valid_r[40];
assign w_valid[49] = w_valid_r[41];
assign w_valid[50] = w_valid_r[42];
assign w_valid[51] = w_valid_r[43];
assign w_valid[52] = w_valid_r[44];
assign w_valid[53] = w_valid_r[45];
assign w_valid[54] = w_valid_r[46];
assign w_valid[55] = w_valid_r[47];
assign w_valid[56] = w_valid_r[48];
assign w_valid[57] = w_valid_r[49];
assign w_valid[58] = w_valid_r[50];
assign w_valid[59] = w_valid_r[51];
assign w_valid[60] = w_valid_r[52];
assign w_valid[61] = w_valid_r[53];
assign w_valid[62] = w_valid_r[54];
assign w_valid[63] = w_valid_r[55];
其中比较关键的变量还有 num 表示计算的次数。