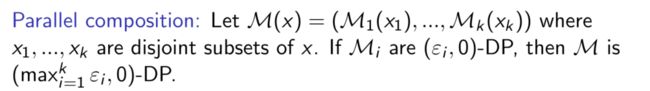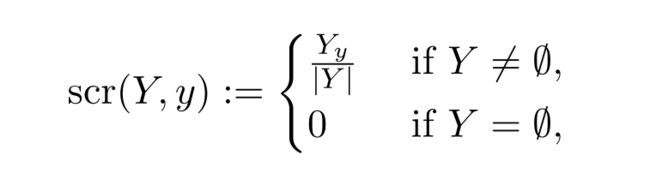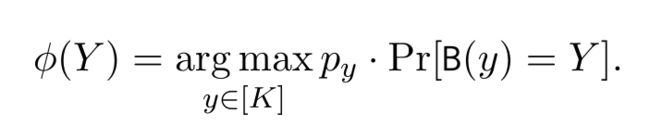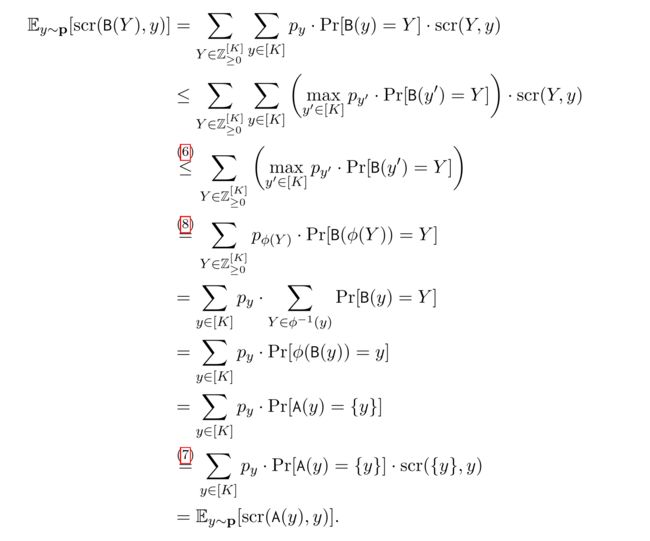On Deep Learning with Label Differential Privacy 深度学习中的本地差分隐私技术的应用和改进
On Deep Learning with Label Differential Privacy
链接: (1) Ghazi, B.; Golowich, N.; Kumar, R.; Manurangsi, P.; Zhang, C. On Deep Learning with Label Differential Privacy. arXiv preprint arXiv:2102.06062 2021.
.
这里写目录标题
- On Deep Learning with Label Differential Privacy
-
- 0. Abstract
- 1. Introduction
-
-
-
- 背景
- 1.1 Label DP
-
- 举例
- Our Contributions
-
-
- 2. Preliminaries
-
-
-
- Definition 2.1 （Differential Privacy）
- Definition 2.2 （Label Differential Privacy）
- [K]
-
-
- 3. Training Algorithms
-
- 3.0 GRR
-
- 3.1.1 v.s. DP-SGD
- 3.1 Multi-Stage Training
-
- 3.1.1 Algorithm Introduction
-
- 初始设置
- 在每一轮 t ∈ [ T ] t\in[T] t∈[T](iteration)
- LP-MST (Label Privacy Multi-Stage Training)
- 3.1.2 Observation
-
- 证明
- 3.2 RR with Prior
-
-
- 已知
- 目标
- 约束
- 3.2.1 RRWithPrior Description
-
- RRTop-k
- RRWithPrior
- 3.2.2 Optimality of RRWithPrior
-
- Obj~p~ (R)
- Lemma 4
- 证明
-
- 3.3 Optimality of RR for Maximizing Quality Score
-
- 3.3.1 Quality Score
-
- Assumption 5
- Example
- 3.3.2 RR 是 求最优Quality Score 的最优算法
-
- Lemma 6
- 证明
- 结果展示
- 4. Evaluation
-
- 4.1 Experimental Setup
-
-
- 数据集
- 深度学习模型架构
- 训练参数设置
- Learning with Noisy Labels
- Multi-Stage Training
-
- 4.2 Result
- 4.3 Robustness to Hyperparameters
-
-
- Data Splits
- Prior Temperature
- Accuracy of Stage-1
- Mixup Regularization
-
- 4.4 Training Beyond Two Stages
- 5. Removal/ Addition Label DP
-
-
-
- Random Response
-
-
- 6. Convex ERM with LabelDP
-
-
-
- 参数设置
- 目标函数
- 损失函数的假设
-
- 6.1 Label-Private SGD
-
- 6.1.1 DP-SGP v.s. LP-SGD
-
- DP-SGD
- LP-SGD
-
- 7. Conclusion and Future Directions
本文主要贡献是在多分类深度学习任务中，提出了一个使用label differential privacy 的深度学习算法，实现了在提高准确率的同时，保证了隐私性，同时该算法利用了每一轮训练的结果作为先验知识，提高下一轮训练的准确率
0. Abstract
- 训练大规模的深度学习模型任务中，实现不泄露敏感信息的同时，不影响准确率，一直是一项重大的挑战
- 将标签Label看作敏感信息，认作需要被保护
- 用理论结果补充了算法，表明在凸经验风险最小化的设置下，Label-DP训练的样本复杂度是与维度无关的，这与普通的差分隐私形成了对比。
1. Introduction
背景
- 机器学习收集大量数据用于分析，使得人们对在模型训练中使用被使用的个人数据隐私产生担忧
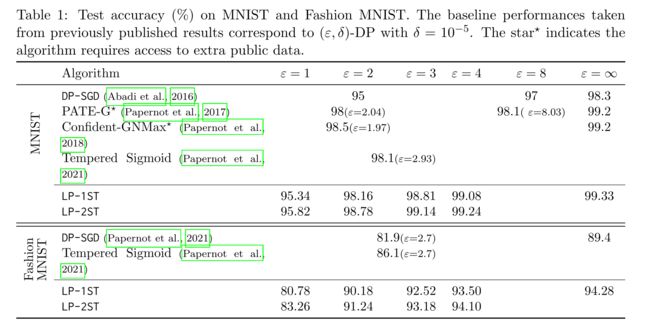
- 差分隐私Differential Privacy被广泛部署应用在机器学习模型训练中，但如DP-SGD一类的模型训练精度仍远低于无DP约束的模型训练结果（准确率-DP-SGD：73%，准确率 non-DP：95%）
1.1 Label DP
- 标签Label被认为是敏感的，而输入被认为不是敏感的，只需要保护Label的隐私
举例
-
computational advertising
-
recommendation systems
-
users surveys and analytics
Our Contributions
- 提出了一个新的基于Label DP的阶段深度学习算法，并对其性能进行了测试
- 得到了一个带有先验知识Prior的经典随机响应-（General Random Respond）GRR算法——RR with Prior
- DP-SGD对于模型大小的伸缩性很差，但是新的算法能够应用在最先进的深度学习框架中，比如ResNet
- 实验证明：保护标签要比保护输入特征和标签来得容易，同时对于经验风险凸优化的情况，Label-DP算法的复杂度远小于同时对特征和标签同时执行DP的复杂度，Label-DP实现了于维度无关的界限
2. Preliminaries
Definition 2.1 （Differential Privacy）
对于任一两个只相差一条数据的邻接数据库D和D’ ，和对任一输出集A的子集S都有
P r [ A ( D ) ∈ S ] ≤ e ε ⋅ P r [ A ( D ’ ) ∈ S ] + δ Pr\lbrack A(D)\in S\rbrack \le e^{\varepsilon} \cdot Pr\lbrack A(D^{’})\in S\rbrack + \delta Pr[A(D)∈S]≤eε⋅Pr[A(D’)∈S]+δ
Definition 2.2 （Label Differential Privacy）
对于任一仅在label上相差一条数据的训练集D和D’ ，和对任一输出集A的子集S都有
P r [ A ( D ) ∈ S ] ≤ e ε ⋅ P r [ A ( D ’ ) ∈ S ] + δ Pr\lbrack A(D)\in S\rbrack \le e^{\varepsilon} \cdot Pr\lbrack A(D^{’})\in S\rbrack + \delta Pr[A(D)∈S]≤eε⋅Pr[A(D’)∈S]+δ
[K]
对于任何的正整数 K, 令 [K] := {1, . . . , K}. [K] 表示标签集
3. Training Algorithms
描述了一个基于Label-DP的深度学习算法
3.0 GRR
对每个Label y i y_i yi使用GRR生成一个隐私的随机Label y i ~ \widetilde{y_i} yi
\
GRR机制的具体实现
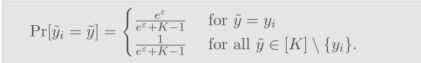3.1.1 v.s. DP-SGD
DP-SGD 每一轮训练都梯度进行新的查询，即进行一次DP算法
而我们的算法只需要对标签进行一次DP算法，后续重复使用
3.1 Multi-Stage Training
直观上：
- 在一小部分的训练数据集（已GRR）训练模型，使其达到一定的准确率
- 任何用该模型对剩余的样本进行预测
3.1.1 Algorithm Introduction
初始设置
-
算法A 输出 概率分类器，给定一个unlabel的样本x，可以给每个类y∈[K]分配一个概率py
-
将数据集S划分为不相交的S(1), ……, S(T)
-
并设置第0轮（初始）模型的M0，给说所有的类输出相同的概率分布
在每一轮 t ∈ [ T ] t\in[T] t∈[T](iteration)
- 使用上一轮训练得到的模型M(t-1) ，为S(t)中的每一个样本xi分配对应的概率(p1, . . . , pK)
- 利用得到的概率 p ⃗ \vec{p} p 帮助RR更加准确，即进行RRWithPriorp算法，见3.2节
- 通过RRWithPriorp得到 y ~ \widetilde{y} y ，使用所有经过随机响应的数据集 S ~ ( 1 ) , … … , S ~ ( t ) \widetilde{S}^{(1)}, ……, \widetilde{S}^{(t)} S (1),……,S (t)（即前t轮全部）训练得到模型 M(t)
个人总结
- 每一轮的RR 都通过上一轮的模型结果M(t-1) 得到关于本轮需要进行RR的数据集的先验知识，即概率分布 来改进本轮RR的准确率 【每一轮的先验知识随着训练也越来越准确】
- 每一轮的模型训练算法A 都使用前t轮经过RR的数据集（随着每一轮的训练扩大数据集），得到新一轮的模型 M(t) 【每一轮的模型随着更准确数据集的占比的扩大也越来越准确】
LP-MST (Label Privacy Multi-Stage Training)
-
multi-stage多阶段算法的第t 阶段，即表示为第t轮
此处多阶段multi stage算法即为 多轮训练算法
-
LP-1ST表示算法的第一轮，LP-2ST表示算法的第二轮，以此类推
-
LP-1ST等价于使用普通的RR算法
3.1.2 Observation
对任意的 ε > 0, 如果RRWithPrior满足ε-DP, 则 LP-MST 满足 ε-LabelDP.
证明
组合性
3.2 RR with Prior
已知
- 关于x的先验概率 p ⃗ = p 1 , . . . , p k \vec{p}={p_1,...,p_k} p=p1,...,pk
- 真实的标签Label y
目标
目标是利用先验概率使得随机化后的标签 y ~ \widetilde{y} y t最大化 输出是正确的概率（等效于最大化信噪比）
约束
对于y算法需要满足ε-DP
3.2.1 RRWithPrior Description
RRWithPrior使用了一个“RRTop-k的子程序”
RRTop-k
(k为预设值，期望输入的尽可能地接近前k个概率大的标签
- 对RR随机响应机制的一个改进，我们只考虑前k个概率最大的标签
- 这里 p ⃗ \vec{p} p是先验知识，根据 p ⃗ \vec{p} p ，集合 Y k Y_k Yk 是标签label i 对应的概率 p ⃗ \vec{p} p中前k个大的label标签
- 如果真实标签 true label y∈Yk，则在集合 Y k Y_k Yk 中使用随机响应
- 否则，我们从这个集合Yk中均等的随机输出一个label标签
Lemma :RRTop-k 满足 ε-DP
证明
对于任何的输入 y , y , ∈ [ K ] y,y^, \in \lbrack K \rbrack y,y,∈[K] 以及任何可能的输出 y ~ ∈ Y k \widetilde{y} \in Y_k y ∈Yk
P r [ R R T o p − k ( y ) = y ~ ] = e ε e ε + k − 1 Pr[RRTop-k(y) = \widetilde{y}]=\frac{e^{\varepsilon}}{e^{\varepsilon}+k-1} Pr[RRTop−k(y)=y ]=eε+k−1eε 当 y = y ~ y=\widetilde{y} y=y ，取到最大
P r [ R R T o p − k ( y , ) = y ~ ] = 1 e ε + k − 1 Pr[RRTop-k(y^,) = \widetilde{y}] = \frac{1}{e^{\varepsilon}+k-1} Pr[RRTop−k(y,)=y ]=eε+k−11当 y , ∈ Y k ∖ y ~ y^, \in Y_k \setminus \widetilde{y} y,∈Yk∖y ，取到最小
对于任何的输入 y , ∉ [ K ] y^, \notin \lbrack K \rbrack y,∈/[K]
P r [ R R T o p − k ( y , ) = y ~ ] = 1 k ≥ 1 e ε + k − 1 Pr[RRTop-k(y^,) = \widetilde{y}] = \frac{1}{k} \ge \frac{1}{e^{\varepsilon}+k-1} Pr[RRTop−k(y,)=y ]=k1≥eε+k−11
that P r [ R R T o p − k ( y ) = y ~ ] P r [ R R T o p − k ( y , ) = y ~ ] ≤ e ε e ε + k − 1 1 e ε + k − 1 = e ε \frac{Pr[RRTop-k(y) = \widetilde{y}]}{Pr[RRTop-k(y^,) = \widetilde{y}]} \le \frac{\frac{e^{\varepsilon}}{e^{\varepsilon}+k-1}}{\frac{1}{e^{\varepsilon}+k-1}}=e^{\varepsilon} Pr[RRTop−k(y,)=y ]Pr[RRTop−k(y)=y ]≤eε+k−11eε+k−1eε=eε
得到如下公式：
RRWithPrior
RRWithPrior 可以被认为是 结合计算 maximizes P r [ R R T o p − k ( y ) = y ] Pr[RRTop-k(y) = y] Pr[RRTop−k(y)=y] 的阈值k 的RRTop-k
计算k值
计算使得 P r [ R R T o p − k ( y ) = y ] = e ε e ε + k − 1 ⋅ ∑ y ~ ∈ Y k p y ~ Pr[RRTop-k(y) = y] = \frac{e^{\varepsilon}}{e^{\varepsilon}+k-1} \cdot \sum_{\widetilde{y} \in Y_k}p_{\widetilde{y}} Pr[RRTop−k(y)=y]=eε+k−1eε⋅∑y ∈Ykpy 最大化的k值
P r [ R R T o p − k ( y ) = y ] = ∑ y ∈ [ K ] p y q y ∣ y = ∑ y ∈ Y k p y q y ∣ y Pr[RRTop-k(y) = y] =\sum_{y\in[K]}p_{y}q_{y|y}=\sum_{y\in Y_k}p_yq_{y|y} Pr[RRTop−k(y)=y]=y∈[K]∑pyqy∣y=y∈Yk∑pyqy∣y
- p y : 由 已 知 概 率 分 布 y ∼ p ⃗ 得 出 p_y:由已知概率分布 y \sim \vec{p}得出 py:由已知概率分布y∼p得出
- q y ∣ y : 表 示 输 入 项 y 经 过 随 机 机 制 R R T o p − k 得 到 得 扰 动 值 仍 未 y 的 概 率 q_{y|y}:表示输入项y经过随机机制RRTop-k得到得扰动值仍未y的概率 qy∣y:表示输入项y经过随机机制RRTop−k得到得扰动值仍未y的概率
- i f y ∉ Y k , q y ∣ y = 0 if\ y \notin Y_k,\ q_{y|y}=0 if y∈/Yk, qy∣y=0
3.2.2 Optimality of RRWithPrior
Objp ®
表示输入标签y 经过随机机制R后 的输出标签仍然为y
O b j p ( R ) = P r y ∼ p [ R ( y ) = y ] Obj_p(R)=Pr_{y\sim p}\lbrack R(y) = y\rbrack Objp(R)=Pry∼p[R(y)=y]
- 已知概率分布 y ∼ p ⃗ y \sim \vec{p} y∼p is P r [ y = i ] = p i f o r a l l i ∈ [ K ] Pr[y = i] = p_i \ \ \ for \ all \ i \in [K] Pr[y=i]=pi for all i∈[K].
Lemma 4
设p为[K]上的任一概率分布，并且R是满足 ε − D P \varepsilon-DP ε−DP 的算法，则有
O b j p ( R R W i t h P r i o r ) ≥ O b j p ( R ) . Obj_p(RRWithPrior) ≥ Obj_p(R). Objp(RRWithPrior)≥Objp(R).
证明
令 q y ~ ∣ y = P r [ R ( y ) = y ~ ] q_{\widetilde{y}|y} = Pr[R(y)=\widetilde{y}] qy ∣y=Pr[R(y)=y ]
则有 O b j p ( R ) = P r y ∼ p [ R ( y ) = y ] = ∑ y ∈ [ k ] q y ∣ y ⋅ p y Obj_p(R)=Pr_{y\sim p}\lbrack R(y) = y\rbrack = \sum_{y\in \lbrack k\rbrack}q_{y|y}\cdot p_y Objp(R)=Pry∼p[R(y)=y]=∑y∈[k]qy∣y⋅py
-
∑ y ~ ∈ [ K ] q y ~ ∣ y = 1 , ∀ y ∈ [ K ] , a n d q y ~ ∣ y ≥ 0 , ∀ y ~ , y ∈ [ K ] \sum_{\widetilde{y}\in[K]} q_{\widetilde{y}|y}=1,\ \forall y \in [K], \ \ and \ \ q_{\widetilde{y}|y}\ge0, \forall \widetilde{y}, \ y \in [K] ∑y ∈[K]qy ∣y=1, ∀y∈[K], and qy ∣y≥0,∀y , y∈[K]
ε − D P \varepsilon-DP ε−DP 则保证了如下公式 q y ~ ∣ y ≤ e ε ⋅ q y ~ ∣ y , ∀ y ~ , y , y , ∈ [ K ] q_{\widetilde{y}|y} \le e^{\varepsilon} \cdot q_{\widetilde{y}|y^{,}} \ \ \ \forall \widetilde{y},\ y,\ y^,\ \in[K] qy ∣y≤eε⋅qy ∣y, ∀y , y, y, ∈[K]
得到如下线性规划方程
3.3 Optimality of RR for Maximizing Quality Score
讨论在RR机制上的普适性，如是否可以推广到RAPPOR上
- 上述讨论为1个样本一个随机输出
- Rappor 为了防止hash碰撞设置了多个Bloom Filte 映射到不同的队列，因此一个输入最终会有多个输出
- 暂时还没研究RAPPOR机制有待后续学习
3.3.1 Quality Score
Z ≥ 0 [ K ] × [ K ] → R ≥ 0 \mathcal{Z}^{[K]}_{\ge0} \times [K] \to \mathcal{R}_{\ge0} Z≥0[K]×[K]→R≥0
- 输入：一个 multiset Y (为RAPPOR中一个真实标签对应的多个输出值集合) 和 真实标签 y ∈[K]
- 输出：分数 scr(Y,y)≥0
Assumption 5
- 第一个条件确保：关于每个Y的score被适当的缩放
- 避免场景：|Y|激励算法输出不必要的 大集合 multiset Y时，quality score 随着|Y| 激增
- 第二个条件确保：当真实标签y的输出值集合为{y}时，quality score 达到最大
Example
-
在第3节中推导的RRWithPrior 可能如下
-
另一种比较好的设置
- Y y Y_y Yy表示Y中y出现的次数
3.3.2 RR 是 求最优Quality Score 的最优算法
Lemma 6
对任一 优良的quality score， 任一先验p， 和任一ε>0， 都有一个ε-DP算法 A 在所有的ε-DP算法， 最大化 E y ∼ p [ s c r ( B ( y ) , y ) ] ， 且 该 算 法 的 输 出 集 合 大 小 总 为 1 E_{y\sim \textbf{p}}[scr(B(y),y)]，且该算法的输出集合大小总为1 Ey∼p[scr(B(y),y)]，且该算法的输出集合大小总为1
证明
令B为任一能最大化 E y ∼ p [ s c r ( B ( y ) , y ) ] E_{y\sim \textbf{p}}[scr(B(y),y)] Ey∼p[scr(B(y),y)]，且能满足ε-DP的算法，则可将其转化为想要的算法A，证明如下
-
得到在先验p下，能够最大概率映射到Y的真实概率y
-
令算法A设置如下： 首先运行算法B获得集合Y，然后输出 $ {\phi(Y) }$，由于后处理算法的特性，算法A也时一个满足 ε-DP的算法，且可得如下推导过程
推导得的算法A即为引理中即能$ 最大化E_{y\sim \textbf{p}}[scr(B(y),y)]，且输出集合大小总为1 的满足ε-DP的算法A$
结果展示
4. Evaluation
4.1 Experimental Setup
数据集
深度学习模型架构
训练参数设置
Learning with Noisy Labels
- 标准化的训练过程会存在过拟合带有噪声的标签，并在测试集上得到很差的泛化结果
- 使用mixup 正则化，在训练期间生成输入和（独热码）标签的随机凸组合，该方法对标签上的噪声有较强的抵抗能力
- 原则上可以使用任何健壮的训练方法，选择mixup只是因为它比较简单
- 近期关于标签噪声的深度学习方法的工作
Multi-Stage Training
-
在multi stage training 中实施 enhancements 增强功能十分有用
- 在multi-stage中使用上一轮训练得到的模型，得到下一轮数据集标签y对应概率p，利用先验概率p，进行RRWithPriorp算法得到对应的扰动值 y ~ \widetilde{y} y ，取RRWithPriorp算法过程中的k值平均值。
- 将前面轮次中 y ~ \widetilde{y} y 不在其top-k概率中的数据全部删除
因为训练的数据都是经过RRWithPrior 扰动后的数据，实施的enhancemens措施主要为：删除前面轮次噪声过大的数据
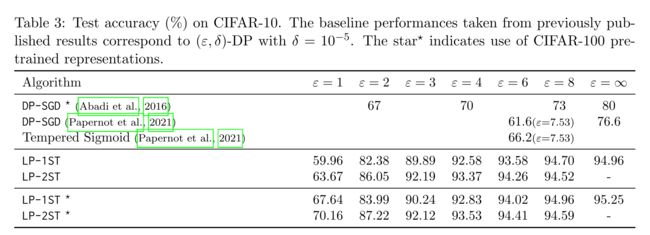
4.2 Result
4.3 Robustness to Hyperparameters
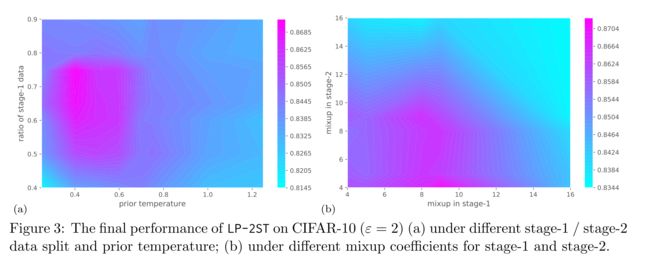
Data Splits
Data Splits：该参数决定了不同训练阶段的数据比例
- 为stage-1分配更多数据有助于为LP-2ST算法学习到更好的先验p
- 但也相对减少了stage-2的训练样本数量，从而降低学习模型的效用
- 在实际应用中，可以为stage-1设置略高于50%的比例
Prior Temperature
-
使用temperature 参数 t t t 修改所学的先验p
-
令 f k ( x ) f_k(x) fk(x)为 输入x上在第k类任务上 关于学得的先验模型 的logits预测
-
如果将prior稀疏化，t大于1通常没有帮助的
Accuracy of Stage-1
理想情况下希望在RRWithPrior计算出的k能够满足如下条件：真实标签y 总是在prior p的前top-k的概率里，否则随机响应一定输出一个错误的扰动标签。
实现方法：
- 分配更多数据提高stage-1训练的性能
- 调整temperature t，分散prior，从而有效增加RRWithPrior中计算的k值
这是一个需要折衷考虑的问题，stage-1的准确率过高或过低都不好
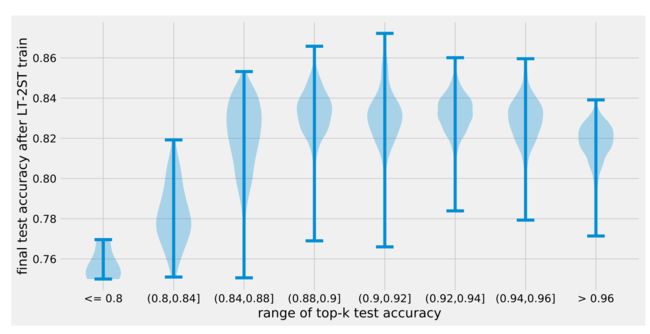
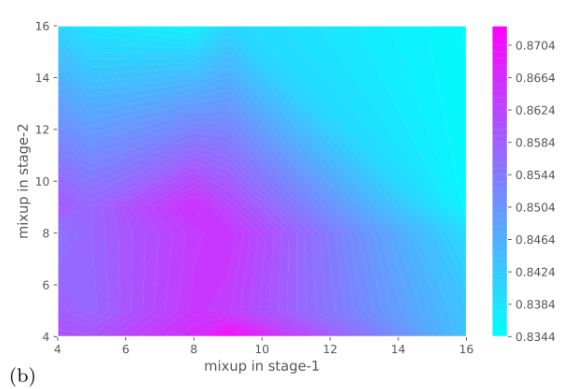
Mixup Regularization
Mixup：控制正则化强度的超参数α，α越大，正则化越强
- 一般α在4-8之间比较好，且如下图所示一般stage-2需要比stage-1相对更少的正则化
- 主要原因是 stage-2的噪声比stage-1的噪声更小
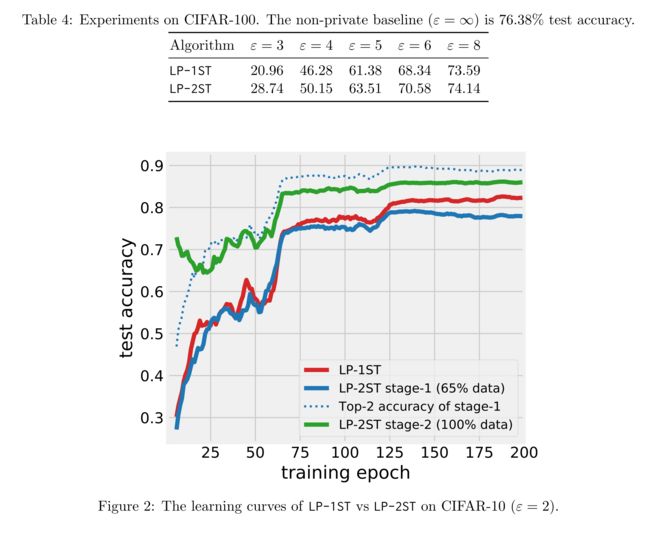
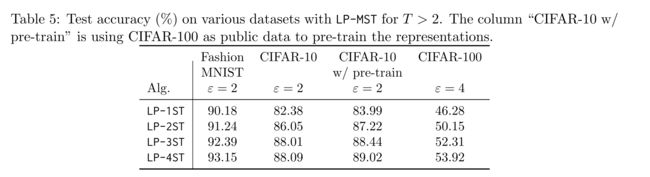
4.4 Training Beyond Two Stages
在1-4 stage 测试精度提高， ＞4的stage会导致某些数据集的收益递减
5. Removal/ Addition Label DP
此部分暂不做深入了解
- removal/addition DP :如果删除/添加一个数据可以实现从一个数据集到另一个数据集，则两个数据集被认为是邻近的
- substitution notion DP: 如果改变一个数据集的一条数据 到另一个数据集，则这两个数据集被认为是邻近的
- Relation :一个满足ε-removal/addition-DP的算法隐私性保证意味着一个满足2ε-substitution-DP的算法隐私性保证
- removal/addition Label DP:可以通过一个像一个数据集中不含有Label标签的数据添加标签 到另一个数据集，则里两个数据集被认为是邻近的
Random Response
6. Convex ERM with LabelDP
参数设置
目标函数
损失函数的假设
推得公式如下：
6.1 Label-Private SGD
此部分大概过了一下，暂未深入阅读推导
6.1.1 DP-SGP v.s. LP-SGD
DP-SGD
LP-SGD
span：由梯度组成的生成空间
- LP-SGD 说明了在n
- 仅对数据集执行单次SGD，T=1，只进行一轮 训练
- 它给每个非零方差的梯度向量添加一个高斯噪声向量，这个梯度向量只对应于每个点的 k 维子空间
- 这意味着，一个典型的噪声矢量的标准只能作为√ k 相对于 bassily 等人(2014)算法的标度√ p。
- LP-SGD v.s. RRWithPrior
7. Conclusion and Future Directions
