第十三届蓝桥杯省赛真题-统计子矩阵

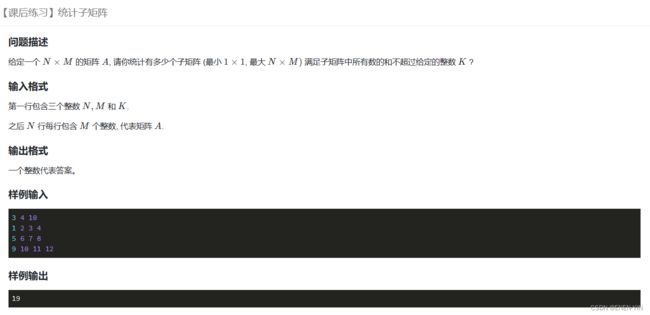
题目

思路

• 30%解法-暴力：复杂度为o($n^6$)
  两层for循环选择起始行、终止行，两层for循环选择起始列、终止列，两层for循环计算和是否小于等于K
• 70%解法-二维前缀和：复杂度为o($n^4$)
  两层for循环选择起始行、终止行，两层for循环选择起始列、终止列
• 100%解法-二位前缀和+尺取法：复杂度为o($n^3$)
  两层for循环选择起始行、终止行，一层for循环尺取列
  ps：尺取法也叫移动窗口法

二维前缀和定义：s[i][j]为从(1,1)到(i,j)这个矩阵的和
画图可以证明：$s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j]$

代码

• 30%解法-暴力

N,M,K = map(int,input().split())
a = [[0]*(M+1)]
for i in range(N):
    a.append([0]+list(map(int,input().split())))
def check(i,j,h,w):
    temp = [a[t][j:j+w] for t in range(i,i+h)]
    if sum(map(sum,temp)) <= K:
        return True
    return False
ans = 0
for i in range(1,N+1):
    for j in range(1,M+1):
        for h in range(1,N-i+2):
            for w  in range(1,M-j+2):
                if check(i,j,h,w):
                    ans += 1
print(ans)

• 70%解法-二维前缀和

import copy
N,M,K = map(int,input().split())
a = [[0]*(M+1)]
for i in range(N):
    a.append([0]+list(map(int,input().split())))
b = [[0]*(M+1) for _ in range(N+1)]
for i in range(1,N+1):
    for j in range(1,M+1):
        b[i][j] = b[i][j-1]+b[i-1][j]-b[i-1][j-1]+a[i][j]
def check(i1,j1,i2,j2):
    temp = b[i2][j2]-b[i2][j1-1]-b[i1-1][j2]+b[i1-1][j1-1]
##    print(i1,j1,i2,j2,temp)
    if temp <= K:
        return True
    return False
ans = 0
##print(b)
for i1 in range(1,N+1):
    for i2 in range(i1,N+1):
        for j1 in range(1,M+1):
            for j2 in range(j1,M+1):
                if check(i1,j1,i2,j2):
                    ans += 1
print(ans)

• 100%解法-二位前缀和+尺取法

N,M,K = map(int,input().split())
a = [[0]*(M+1)]
for i in range(N):
    a.append([0]+list(map(int,input().split())))
b = [[0]*(M+1) for _ in range(N+1)]
for i in range(1,N+1):
    for j in range(1,M+1):
        b[i][j] = b[i-1][j]+b[i][j-1]-b[i-1][j-1]+a[i][j]
def getsum(i1,j1,i2,j2):
    return b[i2][j2]-b[i2][j1-1]-b[i1-1][j2]+b[i1-1][j1-1]
ans = 0
for i1 in range(1,N+1):
    for i2 in range(i1,N+1):
        j1 = 1
        for j2 in range(1,M+1):
            while getsum(i1,j1,i2,j2) > K:
                j1 += 1
            if getsum(i1,j1,i2,j2) <= K:
                ans += (j2-j1+1)
                    
print(ans)