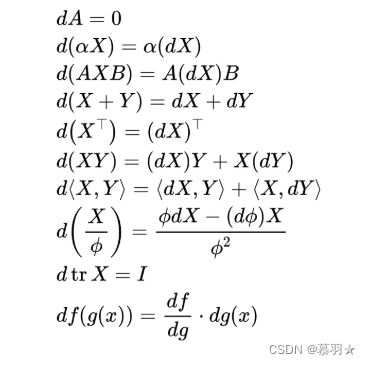机器人中的数值优化(一)—— 数学优化、凸集合与凸函数
本系列文章主要是我在学习《数值优化》过程中的一些笔记和相关思考,主要的学习资料是深蓝学院的课程《机器人中的数值优化》和高立编著的《数值最优化方法》等,本系列文章篇数较多,不定期更新,上半部分介绍无约束优化,下半部分介绍带约束的优化,中间会穿插一些路径规划方面的应用实例
一、数学优化问题
1、最优化问题描述
最优化问题可以描述成,在满足等式约束和不等式约束的前提下,求取使得目标函数值最小的最优解 x ∗ x^{*} x∗,即:
min f ( x ) :s.t. g ( x ) ≤ 0 , h ( x ) = 0 \min f(x):\text{s.t.}g(x)\le0,h(x)=0 minf(x):s.t.g(x)≤0,h(x)=0
其中:
注1:最优解 x ∗ x^{*} x∗,是一个解集,可能包含一个解、多个解,也有可能不存在
注2: f ( x ) \ f(x) f(x)、 g ( x ) \ g(x) g(x)、 h ( x ) \ h(x) h(x)可以是非光滑的,但必须是连续的
2、前提假设
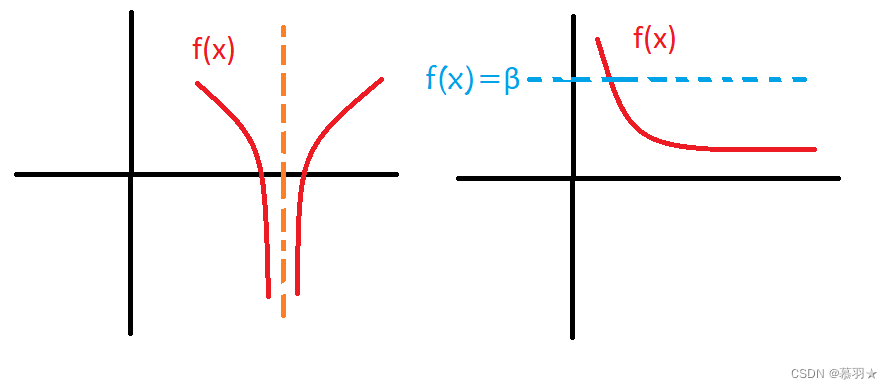
假设1:选取的目标函数是有下界的( lower bounded),即 f ( x ) > = α \ f(x)>=α f(x)>=α
目标函数的最小值可以很小但必须有界 ,因此,目标函数不能存在负无穷的值,若存在负无穷的值会使得最小值无法在计算机中用浮点数表示。
假设2: f ( x ) < = β \ f(x)<=β f(x)<=β时,x是有界的,即保证最优解在x的有限范围内取到
目标函数不能存在当x趋于无穷时函数趋于某个值即下水平集(sub-level sets)无界,这同样会导致最小值无法用浮点数表示。
如下图中的 f ( x ) \ f(x) f(x)分别不满足假设1、假设2
3、非凸优化中的凸性质
为什么我们需要知道凸性?
(1)研究凸集上凸函数的优化问题,关于凸优化问题的研究更成熟。
(2)即使是一些非凸的优化问题,也需要一些凸的性质去分析它的收敛性、稳定性等
(3)对于一些重要的问题,我们可以把非凸问题,进行等价转换,或者近似成凸的问题
(4)很多非凸问题,它的局部是凸的,可以用凸函数对非凸函数进行较好的逼近,如下图的例子所示
(5)在实践中,非凸函数的局部极小值可以是足够好的解。
二、凸集合与凸函数
1、凸优化和非凸优化
在最优化问题中求取 x ∗ ∈ χ x^{*}\in \chi x∗∈χ ,使 f ( x ∗ ) = m i n { f ( x ) : x ∈ χ } f(x^{*} )=min\{f(x):x\in \chi \} f(x∗)=min{f(x):x∈χ} ,其中 x 是n维向量, χ \chi χ是 x 的可行域, f f f 是 χ \chi χ 上的实值函数。凸优化 问题是指 χ \chi χ是 闭合的凸集 ,且 f f f 是 χ \chi χ上的 凸函数 的最优化问题,这两个条件任一不满足则该问题即为非凸的最优化问题。
其中, χ \chi χ是 凸集是指对集合中的任意两点 x 1 , x 2 ∈ χ x_{1},x_{2}\in \chi x1,x2∈χ,有 t x 1 + ( 1 − t ) x 2 ∈ χ , t ∈ [ 0 , 1 ] tx_{1}+(1-t)x_{2}\in \chi,t\in[0,1] tx1+(1−t)x2∈χ,t∈[0,1],即任意两点之间到的连线段都在集合内,直观上就是集合没有“凹下去”的部分。至于闭合的凸集,可以简单地认为是指包含有所有边界点的凸集。
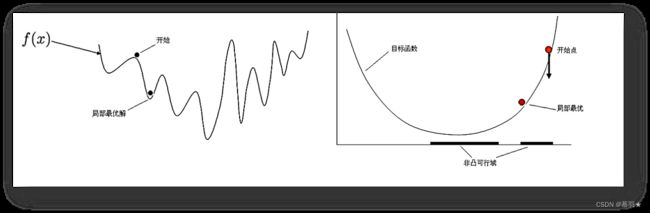
凸优化问题中局部最优解同时也是全局最优解,这个特性使凸优化问题在一定意义上更易于解决,而一般的非凸最优化问题相比之下更难解决,所以常把非凸问题转化成凸问题解决。
若目标函数是下面左图所示的非凸函数,则局部最优解不是全局最优解,可能无法获取全局最优解,若x的集合 χ \chi χ是非凸集合,则会导致如下面右图所示的局部最优解出现。
下图中还给出了凸集合更一般化的描述,在凸集合中任取多个点,如取x1、x2、x3,则表达式 ∑ θ i x i = θ 1 x 1 + θ 2 x 2 + θ 3 x 3 \sum\theta_ix_i=\theta_1x_1+\theta_2x_2+\theta_3x_3 ∑θixi=θ1x1+θ2x2+θ3x3,表示下图所示的蓝色区域(这个蓝色区域称为一个凸组合),其必然位于凸集合中,即蓝色区域是凸集合的子集,其中 ∑ θ i = θ 1 + θ 2 + θ 3 = 1 , θ i ≥ 0 ∀ i \sum\theta_{i}=\theta_{1}+\theta_{2}+\theta_{3}=1,\quad\theta_{i}\geq0\forall i ∑θi=θ1+θ2+θ3=1,θi≥0∀i, θ \theta θ称为重心坐标。
2、凸包与凸集的一些实例
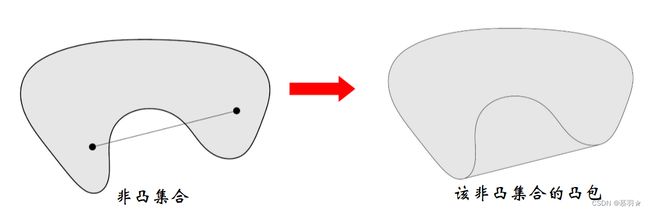
下图的例子中,第一个图中集合中任意两点间连线均位于集合中,是凸集合,第二个图中任意两点间连线存在不属于集合的线段,因此,是非凸集合,第三个图中,因为集合的边界部分缺失,导致相邻两个顶点间连线会有一部分线段不属于集合,因此,为非凸集合。
集合中所有点的凸组合,称为凸包,凸包可以理解为找一个最小的凸集把当前集合包起来,即凸包是包含集合本身最小的一个凸集,对于凸集合而言,凸包就是他本身,而对于非凸集合而言,非凸集合是其凸包的子集,如下图所示:
一些重要的实例如下:
3、凸集间运算对凸性的影响
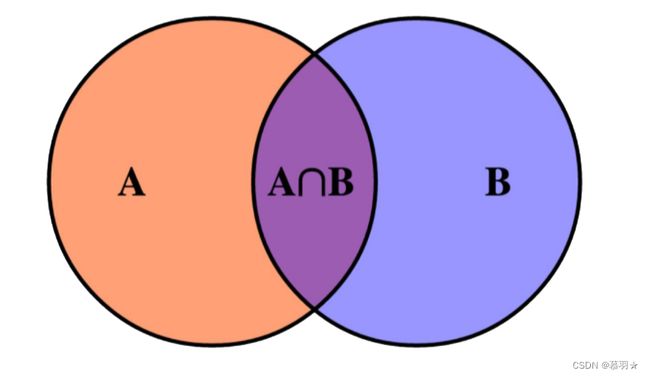
(1)两个凸集的交集一定是凸的,如下图所示:
上述结论可以用来证明一些集合是凸的,如下图所示的两个例子:
(2)两个凸集的加集也是凸集
A + B = { x + y ∣ x ∈ A , y ∈ B } \begin{aligned}A+B=\{x+y\mid x\in A,y\in B\}\end{aligned} A+B={x+y∣x∈A,y∈B}
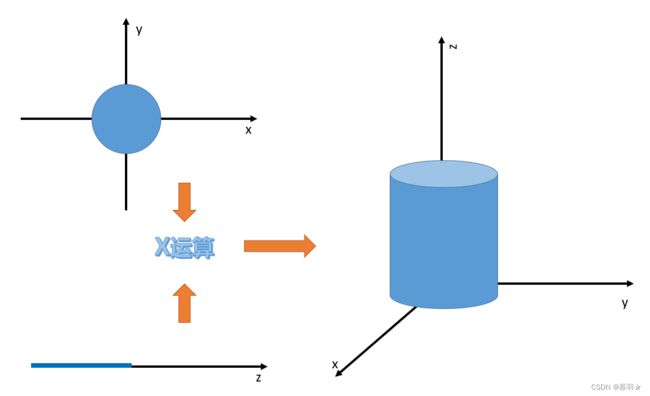
(3)两个凸集的“乘”(组合),也是凸集
A × B = { ( x , y ) ∣ x ∈ A , y ∈ B } \begin{align*}A\times B=\{(x,y)\mid x\in A,y\in B\}\end{align*} A×B={(x,y)∣x∈A,y∈B}
这里的乘,可理解为维数的叠加,如下图中的例子所示,一个二维的集合(圆)与一个一维的集合(线段)进行“乘”运算后变成一个三维的集合(圆柱体):
(4)两个凸集的并集不一定是凸集
A ∪ B A \cup B A∪B
4、函数的高阶信息
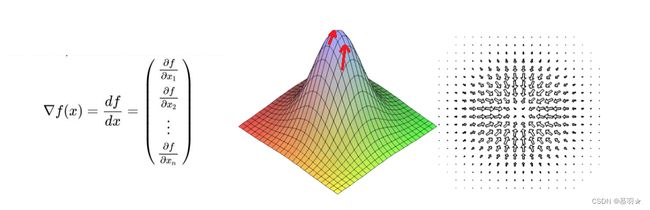
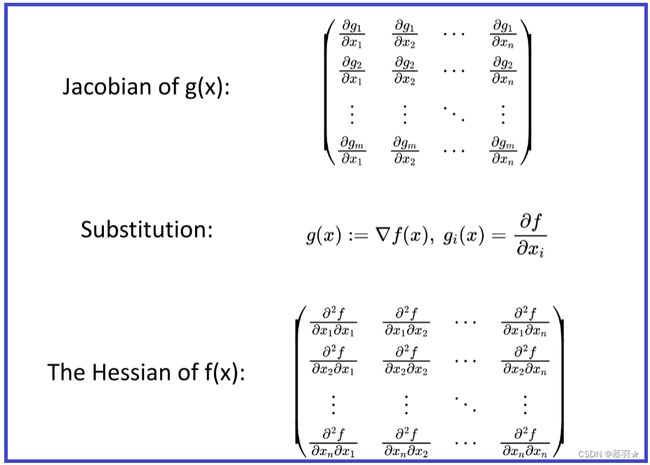
对于一个高维函数而言,其梯度Gradient是依次对每个变量求偏导后组成的向量,二阶梯度Hessian是对Gradient向量中每个元素再分别对每个变量求偏导后组成的矩阵,如下图中的表达式所示,对光滑的函数而言,Hessian矩阵是对称矩阵
常用二阶的泰勒展开式对函数进行近似:
f ( x + △ x ) = f ( x ) + x T ∇ f ( x ) + 1 2 x T ∇ 2 f ( x ) △ x + O ( ∥ △ x ∥ 3 ) f(x+△x)=f(x)+x^{T}\nabla f(x)+\frac{1}{2}x^{T}\nabla^{2}f(x)△x+O\Big(\|△x\|^{3}\Big) f(x+△x)=f(x)+xT∇f(x)+21xT∇2f(x)△x+O(∥△x∥3)
梯度向量 ∇ f ( x ) \nabla f(x) ∇f(x)表示最陡的上升方向。因此,负梯度向量 − ∇ f ( x ) -\nabla f(x) −∇f(x)向量是指函数在点上最陡下降的方向。此外,梯度向量总是与点上的等高线正交,即梯度是沿着等高线垂直的,梯度函数是多对一的: f ( x ) : R n → R f(x):\mathbb{R}^{n}\rightarrow\mathbb{R} f(x):Rn→R。
Hessian矩阵同样是多对一的 R n → R \mathbb{R}^{n}\rightarrow\mathbb{R} Rn→R,而雅可比矩阵Jacobian是多对多的 R n → R m \mathbb{R}^{n}\rightarrow\mathbb{{R}^{m}} Rn→Rm
若取g(x)为f(x)的梯度,则g(x)的雅可比矩阵Jacobian,其实就是f(x)的Hessian矩阵,如下所示:
很多优化问题中涉及的函数不仅仅是多对一的函数,自变量、因变量都可以是标量、向量、矩阵。对应的梯度的结构也有所不同,如下图所示,其中我们用的最多的是:自变量是 R n \mathbb{R}^{n} Rn的,因变量是 R m \mathbb{{R}^{m}} Rm的,而梯度是 R n ∗ m \mathbb{R}^{n*m} Rn∗m的,即雅克比形式。
下图给出了一些微分求导的例子:
在下面的网站中整理了常用的一些运算公式
https://en.wikipedia.org/wiki/Matrix_calculus
下图给出了两个微分求导例子,第一个使用的是按元素求导的方法,第二个使用的是公式法。
参考资料:
1、机器人中的数值优化
2、凸优化和非凸优化