Leetcode 第1342题：将数字变成 0 的操作次数 （位运算解题法详解）

前言

Leetcode第1342题如果用直观方式来做，其实是一道难度极低的题目。但是如果采用位运算的方式来解，则会涉及许多有趣的衍生知识点，了解其背后的原理对我们认识位运算有很大的帮助。现在，就让我们从Leetcode官方的题目描述开始吧。

---

Leetcode 第1342题：将数字变成 0 的操作次数

给你一个非负整数 num ，请你返回将它变成 0 所需要的步数。 如果当前数字是偶数，你需要把它除以 2 ；否则，减去 1 。

示例 1：

输入：num = 14
输出：6
解释：
步骤 1) 14 是偶数，除以 2 得到 7 。
步骤 2） 7 是奇数，减 1 得到 6 。
步骤 3） 6 是偶数，除以 2 得到 3 。
步骤 4） 3 是奇数，减 1 得到 2 。
步骤 5） 2 是偶数，除以 2 得到 1 。
步骤 6） 1 是奇数，减 1 得到 0 。
示例 2：

输入：num = 8
输出：4
解释：
步骤 1） 8 是偶数，除以 2 得到 4 。
步骤 2） 4 是偶数，除以 2 得到 2 。
步骤 3） 2 是偶数，除以 2 得到 1 。
步骤 4） 1 是奇数，减 1 得到 0 。
示例 3：

输入：num = 123
输出：12

---

方法1：最直观的方法

package main

import (
    "fmt"
)

func main() {

    num := 14
    count := 0

    for num > 0 {
        if num%2 == 0 {
            num = num / 2
        } else {            
            num = num - 1
        }
        count++
    }

    fmt.Println(count)

}

解析：过于简单，阅读即可。

---

方法2：位运算

• 前置基础知识

1. 用位运算判断奇偶数：
   首先我们必须了解什么是 “和” 运算，简单而言：
   指两个二进制位，两位都为1，结果为1，任何一位为0，则结果为0，比如：

“和” 运算有很多有趣的特性，例如将任意整数与 “1” 做和运算，可以判断出这个数是奇数还是偶数比如：
10进制数字5（即二进制0101），0101 & 0001 , 结果为1，因此5是奇数
10进制数字6（即二进制0110），0110 & 0001 ，结果是0，因此6是偶数

用程序表达：

    num := 7

    if num&1 == 1 {

        fmt.Println("奇数")

    } else {

        fmt.Println("偶数")

    }

2. 知识延申
   刚才讲到和运算，是两个位为1结果才为1，此外还有以下几种运算：
   或运算 ： 操作符 | ，表示两个位，任何其中一位为1则结果为1，例如：0001|0010，结果：0011
   异或运算 ： 操作符 ^ ，表示两个位，相同则为1，不同则为0，例如：0001^0010，结果：1100

• 移位运算
  左移：操作符 << ，表示将一个二进制位整体左移，相当于将该数乘以2的n次方，例如：
  10进制数5 (0101), 左移1位变成：10进制数10(1010 ) 即： 5 * 2的1次方 = 10
  10进制数6 (0110), 左移2位变成：10进制数24(0001 1000)，即：6 * 2的2次方 = 24

  右移：操作符 >>，表示将一个二进制位整体右移，相当于将该数除以2，例如：
  10进制数5(0101), 右移一位变成：10进制数2(0010) 即：5 / 2 = 2 (整除不含小数点)
  10进制数6(0110), 右移一位变成：10进制数3(0011) 即：6 / 2 = 3
  注意，无论左移还是右移，均会产生补零问题，不同的是左移不会溢出，而右移则会产生溢出：
  左移在低位补零，例如：1111<<1 则变成：11110（最低位补个0）
  右移在高位补零，例如：1111>>1 则变成：0111，原有的最低位那个1，溢出后被吞掉。

• 小技巧
  在Golang里面，如何通过Printf函数打印不同进制的数字：
  %b 输出标准的二进制格式化
  %c 输出对应的unicode码的一个字符
  %d 输出标准的十进制格式化
  %o 输出标准的八进制格式化
  %q 要输出的值是双引号输出就是双引号字符串；另外一种就是 go 自转义的 unicode 单引号字符
  %x（小写x） 输出十六进制编码，字母形式为小写 a-f
  %X（大写X） 输出十六进制编码，字母形式为大写 A-F
  %U（大写U） 输出Unicode格式

• 回到题目
  用位运算的方法来解这道题，有两个要点：

1. 右移1位代表除2，操作次数加1。

2. 最低位为奇数代表一次减1操作，操作次数加1
   用程序表达：

    num := 14
    count := 0
   
    if num <=0 {return 0}    
   
    for num > 0 {
      count = count + (num & 1) + 1
      num = num >> 1
    }
   
    return count - 1
   

   注意：
   程序并没有用 if 语句对num&1的值进行奇偶判断， 观察这行代码：
   count = count + (num & 1) + 1
   因为右移操作总是固定在执行的，即 count 总是要自增1，
   再看 num&1 这个表达式，其结果如果是奇数，则+1（增加1次操作次数），反之则+0 （不增加操作次数）
   偶数情况：count = count + 0 + 1 （相当于自增1）
   奇数情况：count = count + 1 + 1 （相当于自增2）
   再观察这行代码： count = count - 1
   count的终值为什么需要减少1次呢？

   因为任何一个二进制数的最高位肯定是1，比如：0010 这个二进制数，从数值的角度而言，它的前导零没有任何意义（无论10前面有多少个0，它仍然就是10），因此当最后一次右移的时候，判断其为奇数，操作次数加1，此时按照题目要求就应该结束了。但从程序的角度来说，还是要将它右移一次才能触发 num > 0 这个终止条件。因此如果不将这一次操作从总操作次数中去掉，则不符合题目要求。

---

方法3：直接求值

通过方法2，我们可以总结出一个规律：

• 需要做减1操作的次数，其实就是这个数中所有为“1”的个数，
• 需要做除2（右移1位）的次数，就是整体二进制长度减1，即最高位移动到最低位的长度的距离。
  现在以10进制14这个数（1110）为例，
  右移次数：
  1110
  0111 -> 1次
  0011 -> 2次
  0001 -> 3次
  也就是这个二进制数的长度（4-1）次，
  再加上这个二进制位1的数量：3个，
  最终结果3 + 3 = 6 次

C++ 等语言可以用 __builtin_clz 和 __builtin_popcount 这类函数来求出二进制前导零数目和二进制位 1 的个数，遗憾的是并非所有语言都内置有这种函数，比如说Golang就没有，但是我们可以通过算法来实现。

---

一、popcount函数的实现（统计一个二进制位中 “1” 的个数）

首先是popcnt，即算出一个二进制数中有多少个“1”，有非常多的方法实现它，最简单的，可以将这个二进制数转换成一个字符串，遍历之后统计出"1"的个数。稍微进阶一点的，可以用前面说过的num&1配合num>>右移来统计出奇数位（即1）的个数。

另外还有一种极端的以空间换时间的方案，即将所有1个字节（8位）,每个数字(0~255)所对于的个数记录下来，查表就可以了。但是这个方法虽然效率很高，但是对于大数而言就不现实了，因为不可能在程序中放置如此大一张表。

今天我们用分治法来实现这个函数，其他的方法还有很多，如有兴趣可参考以下网址：

参考资料1：https://zhuanlan.zhihu.com/p/147862695
参考资料2：https://zhuanlan.zhihu.com/p/341488123
参考资料3：https://www.geeksforgeeks.org/count-set-bits-in-an-integer/

使用分治法来加速求解二进制数位 1 的个数，算法如下：
对二进制数 num，它的位 为1 的个数等于所有位的值相加的结果，比如：
11010011= 1+1+0+1+0+0+1+1 = 5。

分治法的底层逻辑非常简单，比如我们可以将 8 个位的求和分解成 4 个相邻的位的求和，
然后将 4 个中间结果分解成 2 个相邻的求和，以此类推，如图：

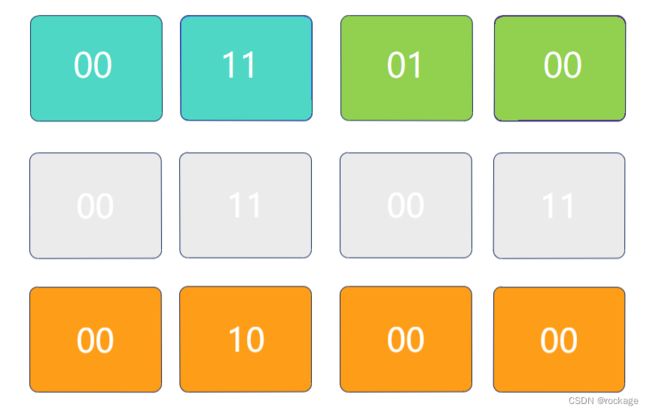
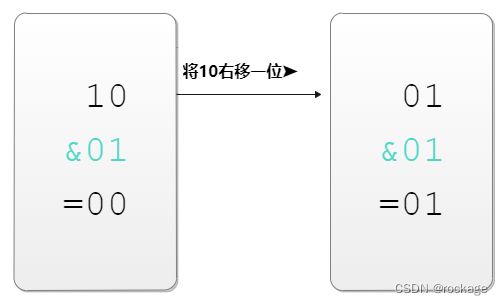
那么，什么是“相邻的位”呢，其实就是指长度为两位（bit)的二进制数，比如以 “10” 为例：

前面我们提到过，可以用num&1来做奇偶数判断，基于同样原理，这里引入一个新的名词称为 ”比特掩码“。为了统计相邻的两个二进制位有多少个1，我们采用 ”01“ 作为比特掩码，

想象一下，如果将 “10” 这个二进制数分成左右两半的话，1在左侧，0在右侧。

首先让 “10” 直接与比特掩码 “01” 做和运算，实际上就是判断"10"的右侧是否为1；

将 “10” 右移一位后，再次与比特掩码 “01” 做一次和运算，相当于判断了"10"的左侧是否为1；

最后，右侧=00，左侧=01，两者相加，即“10” 这个二进制数中有1个 “1” 。

流程如下：

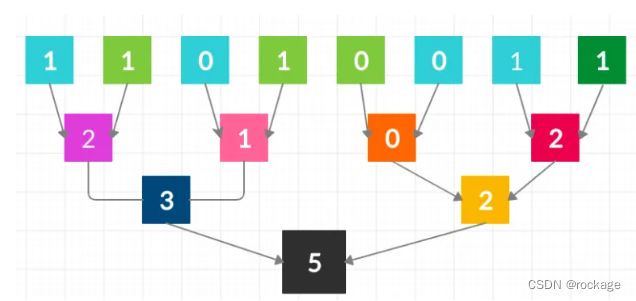
事实上，无论二进制数有多长，总是可以采用将它折成两段的方法分别计算左右两侧的1的个数，再将左右两侧的结果相加统计出所有的“1”。 理解了分治法的底层逻辑后，我们以一个8位二进制数：11010011为例，一步一步观察分治法是如何工作的。

第1步：计算出相邻两位1的个数 （8合为4）

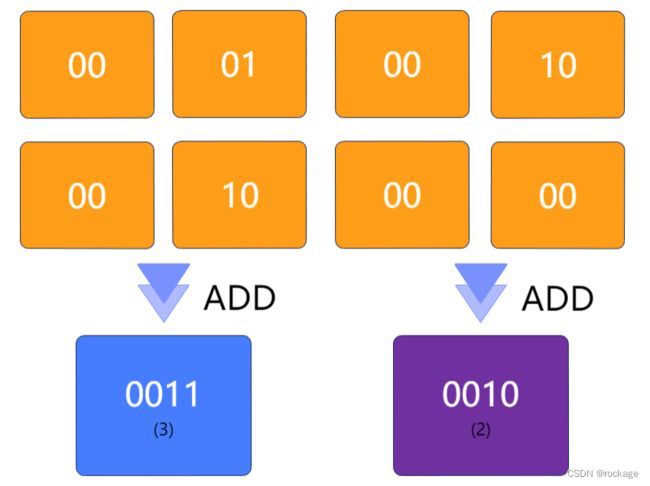
首先用比特掩码 ”01“，对整个二进制位进行”和“运算，其中，

第一行就是要处理的二进制数 11010011 ，按照相邻为一组的方式分成了4组，用不同的颜色加以区分；

第二行（灰色），是用 ”01“ 组成的比特掩码 ；

第三行（橙色），是第一行与第二行做 ”和“ 运算之后的结果。

第一轮“和”运算得到中间结果后，并没有结束，目前为止只计算了相邻两个比特位的其中一半（右侧），另一半（左侧）还没有计算，现在，将11010011向右移动1位，变成：01101001，再与比特掩码做一次和运算：

现在，得到了完整的相邻两个比特位1的个数了，将他们相加（即将橙色两行加起来），就是相邻两个比特位 1 的个数（PS: 为了方便观察括号里为10进制数）：

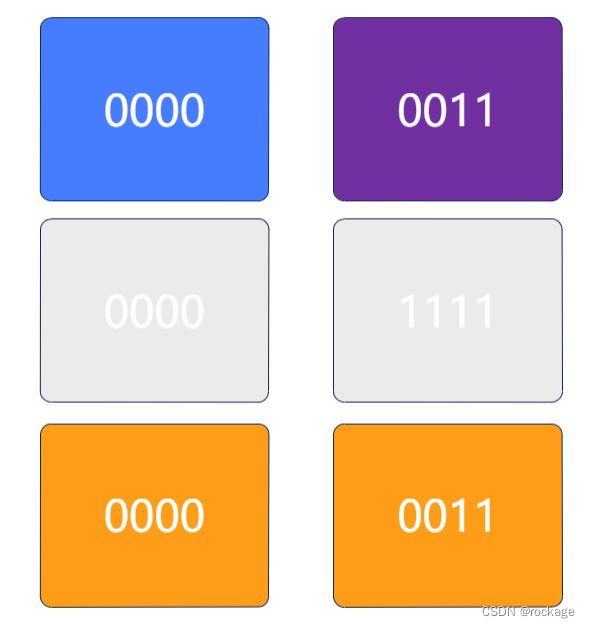
结合最开始出现那幅图，很容易理解，我们已经把一部分工作完成了：

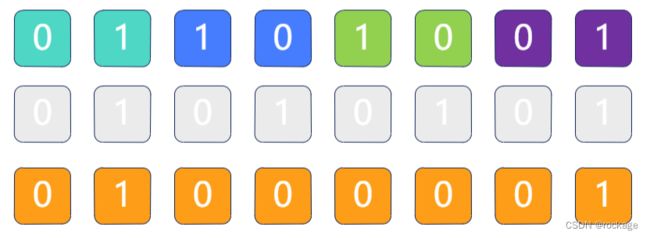
第2步：再次整合（4合为2）

上一步产生中间结果：10、01、00、10 是 2个Bit位，因此在这一步我们需要用比特掩码 “0011” 才能将之完整覆盖。橙色部分为和计算的结果，原理与之前一样：

同理，在进行右移操作的时候，也需要移动2位，即 11010011>>2 = 00110100

接着，跟之前一样，将和运算的结果相加：

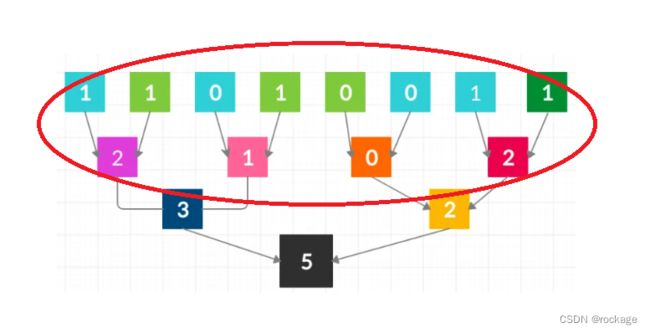
第2步：最后的整合（2合为1）

虽然每一步的计算原理是完全一样的，但必须要提醒的是，随着聚合的比特位越来越多，比特掩码也变得越来越宽 ，现在，因为需要覆盖4个比特位，因此比特掩码也变成了”00001111“，同理右移也需要增加到4位。

首先还是老样子，先映射出右边部分1的个数：

右移4位，然后再映射出左边的1的个数：

将左右两侧结果相加，得到最终结果：

OK，至此我们就将 11010011 这个二进制数里面1的个数统计出来了：5 个。

想象一下，如果我们继续用更大的比特掩码，比如说 “0000000011111111” 再次与上述结果做和运算会发生什么？ 答案是什么也不会发生，因为比特掩码的位数已经超过8位了，任何二进制位与1做和运算其结果等于自身，因此再继续下去尽管没有必要，但也不会影响结果。

---

用程序表达

func popCnt(num uint) int {
    num = num&0x55555555 + num>>1&0x55555555
    num = num&0x33333333 + num>>2&0x33333333
    num = num&0x0F0F0F0F + num>>4&0x0F0F0F0F
    num = num&0x00FF00FF + num>>8&0x00FF00FF
    num = num&0x0000FFFF + num>>16&0x0000FFFF
    return int(num)
}

因为函数的形参num是一个uint无符号整数，它的位长是32Bit，其中，

• 16进制数0x55555555 换算成2进制数为：01010101010101010101010101010101

  也就是我们之前使用过的比特掩码”01“

• 16进制数0x33333333换算成2进制数为：00110011001100110011001100110011

  对应的比特掩码”0011“

• 16进制数0x0F0F0F0F换算成2进制数为：00001111000011110000111100001111

  对应的比特掩码”0000111111“

• 以此类推，一直到0x0000FFFF，则是： 000000000000000011111111111111111

发现规律了吗? 任意长度的32位数，总有将它”罩住“的比特掩码，而任意一个32位数，最多只需要进行5次运算即可得到其中二进制 ”1“ 的个数，因此我们说这个方法的时间复杂度是O（Log32），又因为其只需要常数空间，因此它的空间复杂度是O(1)，效率很高。

---

二、clz 函数的实现（计算一个二进制位的长度）

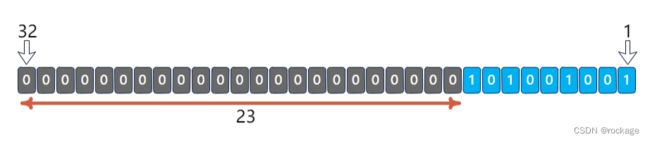
前面提到过，一个 uint 无符号整数，位长为32位，我们只需要算出这个整数的前导零有几个，然后用32减去这些前导0即可。从这个角度而言，计算一个二进制位的长度，相当于就是计算其前导零的个数。如图：

例如 101001001这个二进制数，其长度就是 32 - 23个前导零 = 9位。

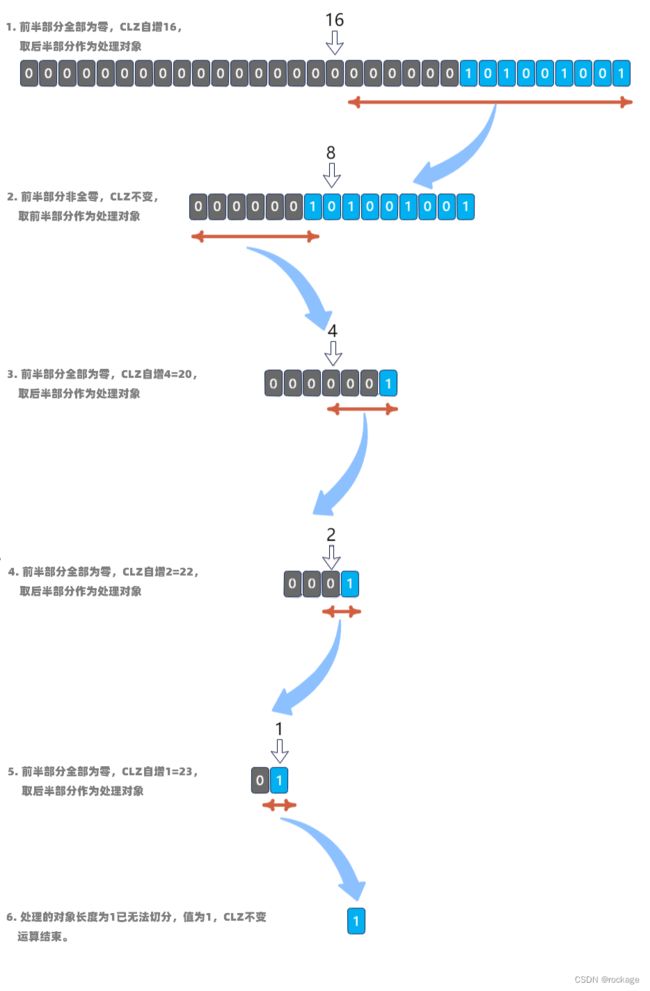
实现这个算法有两种方式，第一种比较简单直观，将 num 做循环左移1位操作，判断最高位是否为1，左移了几次，前导零就有几个。还有另外一种更高效的方法，首先将num一分为二，判断前半部分是否全为零，如果是，则将 clz（前导零计数器） 加上前半部分的长度，然后将后半部分作为处理对象，否则将前半部分作为处理对象。重复以上操作直到处理的对象长度为 1，直接判断是否有零，有则将clz 加 1，如图：

总结而言，这个算法只有两条规则：

1. 前半部分如果为全0，则将其位数计入计数器，取后半部分作为下一步的处理对象；

2. 前半部分如果不是全0，计数器不变，取前半部分作为下一步的处理对象。

如此，任何一个32位无符号整数（uint），无论长短，最多仅需要进行6次计算即可得出其前导零的个数，效率还是很高的。

---

用程序表达：

func bitsLen(x uint) int {
    clz := 0
    if x>>16 == 0 {
        clz += 16
        x <<= 16
    }
    if x>>24 == 0 {
        clz += 8
        x <<= 8
    }
    if x>>28 == 0 {
        clz += 4
        x <<= 4
    }
    if x>>30 == 0 {
        clz += 2
        x <<= 2
    }
    if x>>31 == 0 {
        clz++
    }
    return 32 - clz
}

上面这段代码采用右移的方法来区分前半部分和后半部分的判断的，例如这个判断：

    if x>>16 == 0 {
        clz += 16
        x <<= 16
    }

首先判断 x 右移16位之后的值是否为全0，然后有两种情况：

1. 如果成立，则clz自增16，接着改变 x 的值，将其左移16位，这相当于将 x 的后半部分作为下一步操作对象；

2. 如果不成立，则clz不做改变，也不改变x的值，这就相当于将 x 的前半部分作为下一步操作对象。

---

结语：使用popcount和clz函数重新解题

绕了一大圈，现在让我们将popcount和clz函数用直接位运算的方法将题目重做一遍。

代码如下：

package main

import (
	"fmt"
)

// 计算二进制位的长度
func bitsLen(x uint) int {
	clz := 0
	if x>>16 == 0 {
		clz += 16
		x <<= 16
	}
	if x>>24 == 0 {
		clz += 8
		x <<= 8
	}
	if x>>28 == 0 {
		clz += 4
		x <<= 4
	}
	if x>>30 == 0 {
		clz += 2
		x <<= 2
	}
	if x>>31 == 0 {
		clz++
	}
	return 32 - clz
}

// 统计二进制位中“1”的个数
func onesCount(num uint) int {
	num = num&0x55555555 + num>>1&0x55555555
	num = num&0x33333333 + num>>2&0x33333333
	num = num&0x0F0F0F0F + num>>4&0x0F0F0F0F
	num = num&0x00FF00FF + num>>8&0x00FF00FF
	num = num&0x0000FFFF + num>>16&0x0000FFFF
	return int(num)
}

func main() {
	var num uint
	num = 14

	if num == 0 {
		fmt.Println(0)
	}
	fmt.Println(bitsLen(uint(num)) - 1 + onesCount(uint(num)))
}

---

最后这段代码就不需要再啰嗦什么了，如果你坚持读到了这里并理解了前面的知识点，那么读懂它是不费吹灰之力的，祝大家刷题愉快，也欢迎大家留言评论拍砖！