代码随想录算法训练营第五十三天|1143.最长公共子序列、1035.不相交的线、53.最大子序和 动态规划
day53 2023/03/25
一、最长公共子序列
给定两个字符串 text1 和 text2,返回这两个字符串的最长公共子序列的长度。
一个字符串的 子序列 是指这样一个新的字符串:它是由原字符串在不改变字符的相对顺序的情况下删除某些字符(也可以不删除任何字符)后组成的新字符串。
例如,"ace" 是 "abcde" 的子序列,但 "aec" 不是 "abcde" 的子序列。两个字符串的「公共子序列」是这两个字符串所共同拥有的子序列。
若这两个字符串没有公共子序列,则返回 0。
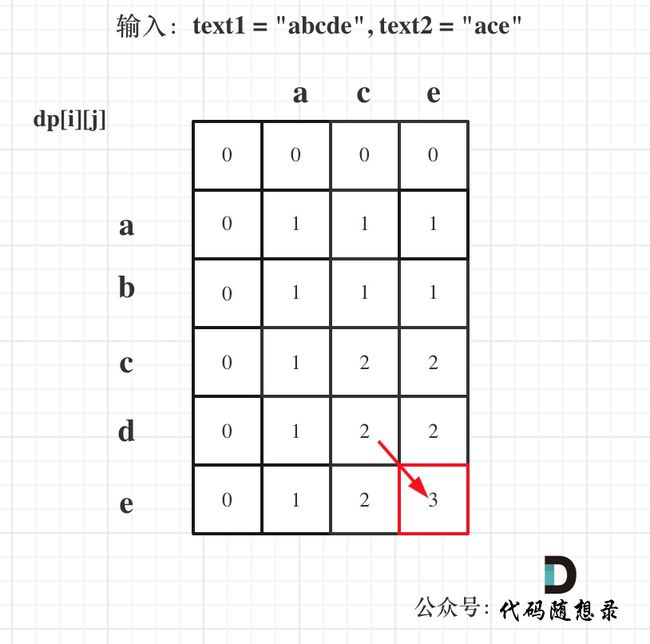
以输入:text1 = "abcde", text2 = "ace" 为例,dp状态如图:
代码如下:
class Solution {
public:
int longestCommonSubsequence(string text1, string text2) {
vector> dp(text1.size() + 1, vector(text2.size() + 1, 0));
for (int i = 1; i <= text1.size(); i++) {
for (int j = 1; j <= text2.size(); j++) {
if (text1[i - 1] == text2[j - 1]) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
return dp[text1.size()][text2.size()];
}
}; 二、不相交的线
我们在两条独立的水平线上按给定的顺序写下 A 和 B 中的整数。
现在,我们可以绘制一些连接两个数字 A[i] 和 B[j] 的直线,只要 A[i] == B[j],且我们绘制的直线不与任何其他连线(非水平线)相交。
以这种方法绘制线条,并返回我们可以绘制的最大连线数。
代码如下:
class Solution {
public:
int maxUncrossedLines(vector& A, vector& B) {
vector> dp(A.size() + 1, vector(B.size() + 1, 0));
for (int i = 1; i <= A.size(); i++) {
for (int j = 1; j <= B.size(); j++) {
if (A[i - 1] == B[j - 1]) {
dp[i][j] = dp[i - 1][j - 1] + 1;
} else {
dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
}
}
}
return dp[A.size()][B.size()];
}
}; 三、最大子序和
给定一个整数数组 nums ,找到一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
代码如下:
class Solution {
public:
int maxSubArray(vector& nums) {
if (nums.size() == 0) return 0;
vector dp(nums.size());
dp[0] = nums[0];
int result = dp[0];
for (int i = 1; i < nums.size(); i++) {
dp[i] = max(dp[i - 1] + nums[i], nums[i]); // 状态转移公式
if (dp[i] > result) result = dp[i]; // result 保存dp[i]的最大值
}
return result;
}
}; 再来几道回溯捏捏,补一下之前欠下的账——棋盘问题
一、n皇后问题
代码如下:
下面我用一个 3 * 3 的棋盘,将搜索过程抽象为一棵树,如图:
//n皇后问题
#include
using namespace std;
vector< vector > result;
int n;
bool check(int row,int col,vector& chessboard,int n)
{
//检查列上是否有皇后
for(int i=0;i=0&&j>=0;i--,j--)
{
if(chessboard[i][j]=='Q')
return false;
}
//检查135°角上是否有皇后
for(int i=row-1,j=col+1;i>=0&&j& chessboard)
{
if(index==n)
{
result.push_back(chessboard);
return;
}
for(int i=0;i chessboard(n,string(n,'.'));
//初始化棋盘
dfs(n,0,chessboard);
for(int i=0;i 二、解数独问题
代码如下:
//解数独问题
#include
using namespace std;
vector< vector > board(9,vector(9,'.'));
//因为这里必须找到一组就返回,所以返回类型不用void
bool check(int row,int col,char val,vector< vector >&board)
{
//先查找列
for(int i=0;i<9;i++)
{
if(board[i][col]==val)
return false;
}
//再查找行
for(int j=0;j<9;j++)
{
if(board[row][j]==val)
return false;
}
//最后查找9方格中是否重复
int startRow=(row/3)*3;
int startCol=(col/3)*3;
for(int i=startRow;i >&board)
{
for(int i=0;i>board[i][j];
}
dfs(board);
for(int i=0;i<9;i++)
{
for(int j=0;j<9;j++)
cout< 再复习一道dp
爬楼梯的最小代价
代码如下:
#include
using namespace std;
const int N=100010;
vector cost;
vector dp(cost.size()+1);//必须将dp数组初始化大小捏
int main()
{
int x;
while(scanf("%d",&x)!=EOF) cost.push_back(x);
dp[0]=0,dp[1]=0;//可以从第0级或者第1级开始爬楼梯
for(int i=2;i<=cost.size();i++)
{
dp[i]=min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);
}
printf("%d\n",dp[cost.size()]);
return 0;
} 不同路径
代码如下:
//不同路径
#include
using namespace std;
int m,n;
//m代表行数,n代表列数
int main()
{
scanf("%d%d",&m,&n);
vector< vector >dp(m,vector(n,0));//注意dp数组应该到主函数里面来
for(int i=0;i 不同路径Ⅱ
代码如下:
//不同路径+有障碍物
#include
using namespace std;
int m,n;
//m代表行数,n代表列数
int main()
{
scanf("%d%d",&m,&n);
vector< vector >obstacle(m,vector(n,0));
vector< vector >dp(m,vector(n,0));//注意dp数组应该到主函数里面来
for(int i=0;i 整数划分代码如下:
//整数拆分
#include
using namespace std;
int n;
int main()
{
scanf("%d",&n);
vectordp(n+1,0);
dp[2]=1;
for(int i=3;i<=n;i++)
{
for(int j=1;j<=i-1;j++)
dp[i]=max(dp[i],max(j*(i-j),j*dp[i-j]));
}
printf("%d\n",dp[n]);
return 0;
} 不同的二叉搜索树
//不同的二叉搜索树
#include
using namespace std;
int n;
int main()
{
scanf("%d",&n);
vectordp(n+1,0);
dp[0]=1;
for(int i=1;i<=n;i++)
{
for(int j=0;j