数学笔记/scipy 笔记：豪斯多夫距离（Hausdorff ）

1 概念

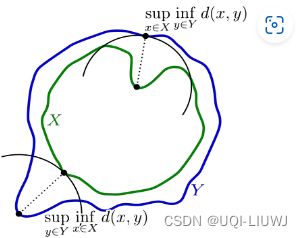
一个点集中的点到另一个点集的最短距离的最大值。 

 

 

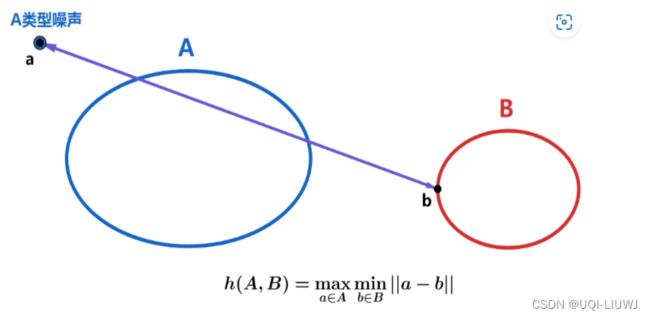
 1.1 容易受噪声的影响

 1.2 性质

• 当A和B都是闭集的时候，Hausdorff距离满足：
  • 

   

2 举例

 

 3 python 实现

3.1 掉包 scipy

3.1.1 数据

from scipy.spatial.distance import directed_hausdorff
u = np.array([(1.0, 0.0),
              (0.0, 1.0),
              (-1.0, 0.0),
              (0.0, -1.0)])
v = np.array([(2.0, 0.0),
              (0.0, 2.0),
              (-2.0, 0.0),
              (0.0, -4.0)])

import matplotlib.pyplot as plt
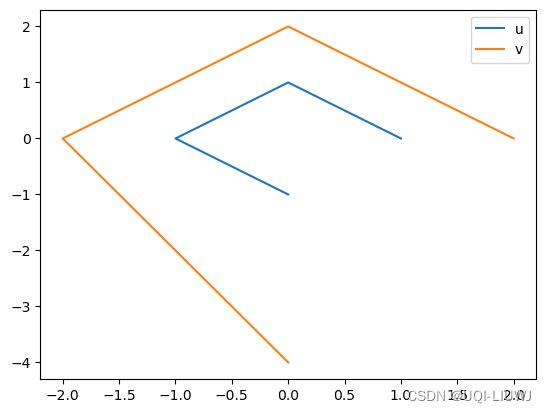
plt.plot(u[:,0],u[:,1],label='u')
plt.plot(v[:,0],v[:,1],label='v')
plt.legend()

3.1.2 scipy 

directed_hausdorff(u, v)
(2.23606797749979, 3, 0)

directed_hausdorff(v,u)
(3.0, 3, 3)

返回的三个元素是什么意思呢？

以（u,v）为例，第一个元素是h(u,v)【单边】,第二个元素是u对应的index，第三个元素是v对应的index。这两个index的连线时最大的最短距离

def distance(x,y):
    return float(np.sqrt((x[0]-y[0])*(x[0]-y[0])+(x[1]-y[1])*(x[1]-y[1])))

ada_matrix=np.zeros((4,4))
for i in range(u.shape[0]):
    for j in range(v.shape[0]):
        ada_matrix[i][j]=distance(u[i],v[j])
ada_matrix
'''
array([[1.        , 2.23606798, 3.        , 4.12310563],
       [2.23606798, 1.        , 2.23606798, 5.        ],
       [3.        , 2.23606798, 1.        , 4.12310563],
       [2.23606798, 3.        , 2.23606798, 3.        ]])
'''