链表噩梦题之一：2条链表相交问题，链表可能有环，也可能无环，求交点

链表噩梦题之一：2条链表相交问题，链表可能有环，也可能无环，求交点

提示：
链表噩梦题也就2个
第二个是约瑟夫环问题！
之前我就写过：
（2）链表噩梦题之二：约瑟夫环问题

---

题目

给定2个链表，head1，和head2
他们可能有环，可能无环
若两个链表相交，请返回相交的第一个交点，否则返回null

---

一、审题

示例：
（1）2个链表都无环
1）俩都无交点，平行的

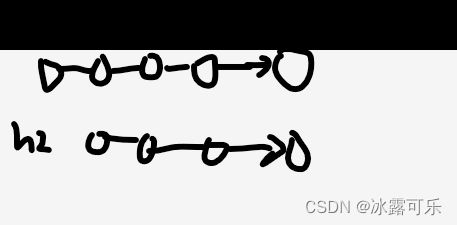
2）俩相交了，最后汇聚到一条链上。

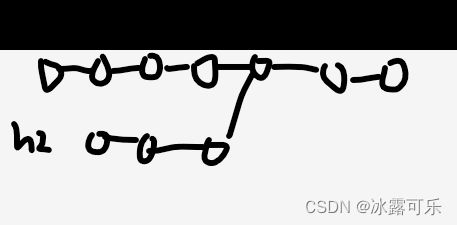
（2）2个链表中，其中一个有环，而另一个无环
其中一个无环，则不可能相交，要是交了，另一个有环那个环也必然是无环链表上的环，岂不矛盾了。

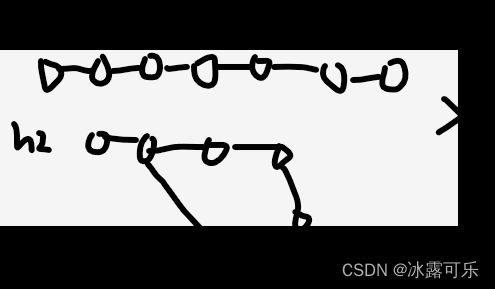
（3）两个链表均有环：
1）俩的环是独立的，压根不相交

2）两个相交，而且入环节点是同一个

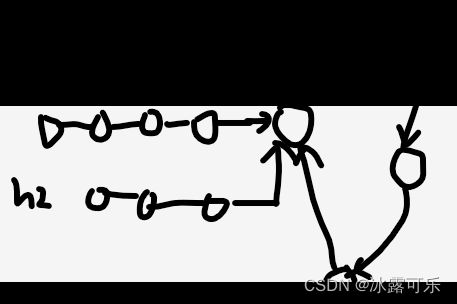
3）2个链表相交，但是入环节点不相同。

请你求上面这些状况下的相交交点

解题思想：

本题中涉及的链表的节点数据结构为：

//基础数据结构，单链表
    public static class Node{
        public int value;
        public Node next;
        public Node(int v){
            value = v;
        }
    }

（1）但凡要求2个链表的交点，就必须给头结点head1和head2，和每一个链表的入环节点loop1和loop2

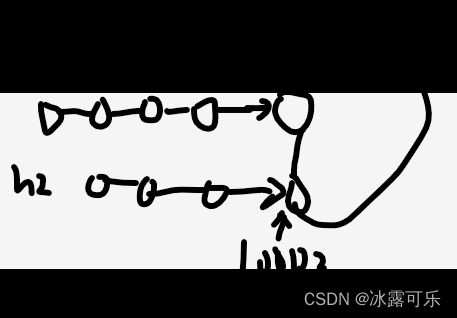
因此，在求交点前，必须单独求链表head1和head2的入环节点：loop1和loop2
这个函数咱们定为：

public static Node getLoopNode(Node head)

（2）当给头结点head1和head2，和每一个链表的入环节点loop1和loop2，请你求交点
咱就得分下面三种情况：
——给你2个链表和他们的入环节点，如果都没有环，求相交点
——给你2个链表和他们的入环节点，如果其中一个有环，而另一个没有环，求相交点
——给你2个链表和他们的入环节点，如果都有环，求相交交点
上面每种情况，都分为相交还是不想交，因此情况复杂，还需要细细分类，这就是所谓的噩梦的原因！！！

经过学习之后，自己画图就能搞明白上面三种情况
我已经是第三次见这个题了，当初第一次学习，初次见面，难！
第二次复习也还好
第三次，见面，也就是这次，我就把它透彻地理解清楚，然后写成博客，加深我的印象。

下面我带你破解这个链表的噩梦题！！！

---

二、给你一个链表，请你求其入环节点

有环就返回入环节点
无环返回null

咱们现在说的只有一个链表！
（1）压根这个链表就无环，返回null

那要怎么判断呢？
也比较容易了，我们让cur依次遍历
遍历过的点，进集合set
往前遍历cur的过程中，每次都要查一下，cur是否曾经出现在set中
如果这个链表，压根没有环，你cur绝对不会遇到2次
遇不到，就无环
遇到了，第一次相遇的入环节点就是cur，其实就是下面（2）的判断方法和求法
——这个方法固然简单，但是！要耗费额外空间复杂度，只适用于笔试！

笔试求AC，不考虑空间复杂度：

//给你一个链表，求这个链表的交点
    public static Node getLoopNodePen(Node head){
        if (head == null || head.next == null) return null;//1个点无法成环

        Set<Node> set = new HashSet<>();
        Node cur = head;
        while (cur != null){
            if (set.contains(cur)) return cur;//见过了，有环，它就是入环节点
            set.add(cur);
            cur = cur.next;
        }

        //一直没见，那就没有入环节点
        return null;
    }

（2）确实，有环，返回入环节点loop
咱们面试可不能这么写，得优化空间复杂度到o(1)
链表的操作，往往要用快慢指针
对于环形链表来说，求入环节点就是一个玄学的数学推理
咱不用推，直接记住以下结论：

（1）初始化快慢指针：slow先走1步，fast先走2步；
（2）如果快指针，先遇到null，则根本就不可能有环，返回null
（3）有环的话，slow和fast一定会相遇，这第一次相遇就证明了有环，就是这么巧！！！
（4）怎么找到那个入环节点呢？让fast回到head，和slow同步慢走（都只走1步），第二次相遇时，这个点，就是入环节点。

绿色是初始化的fast和slow
粉色第一步，橘色第二步，紫色第三步，青蓝第4步，s和f相交，说明有环
然后让f回到head，即红色那，现在开始s和f慢慢走，同步走，发现：
青蓝色s走四步，同时红色fast走四步，他俩相交在同一个点，这个点，就是入环节点。

手撕代码，没啥多说，记住：

//对于环形链表来说，**求入环节点**就是一个玄学的数学推理
    //咱不用推，直接记住以下结论：
    //
    //（1）初始化快慢指针：slow先走1步，fast先走2步；
    //（2）如果快指针，先遇到null，则根本就不可能有环，返回null
    //（3）有环的话，slow和fast一定会相遇，这第一次相遇就证明了有环，就是这么巧！！！
    //（4）怎么找到那个入环节点呢？让fast回到head，和slow同步慢走（都只走1步），第二次相遇时，这个点，就是入环节点。
    public static Node getLoopNodeFace(Node head){
        if (head == null || head.next == null) return null;
        //（1）初始化快慢指针：slow先走1步，fast先走2步；
        Node slow = head.next;
        Node fast = head.next.next;
        //（2）如果快指针，先遇到null，则根本就不可能有环，返回null
        while (slow != fast){
            if (fast.next == null || fast.next.next == null) return null;
            //（3）有环的话，slow和fast一定会相遇，这第一次相遇就证明了有环，就是这么巧！！！
            fast = fast.next.next;
            slow = slow.next;
        }
        //（4）怎么找到那个入环节点呢？
        // 让fast回到head，和slow同步慢走（都只走1步），第二次相遇时，这个点，就是入环节
        fast = head;
        while (slow != fast){
            slow = slow.next;
            fast = fast.next;//同步走
        }
        //第二次相遇，必然是入环节点
        return slow;
    }

测试一把：

//造一条链表
    public static Node createLinkNode1(){
        Node n1 = new Node(1);
        Node n2 = new Node(2);
        Node n3 = new Node(3);
        Node n4 = new Node(4);
        n1.next = n2;
        n2.next = n3;
        n3.next = n4;
        n4.next = n2;//4回指2，说明2是环的交点
        
        return n1;
    }

    public static void test(){
        //测试是否有入环节点，笔试，面试不一样
        Node head = createLinkNode1();
        Node ans = getLoopNodePen(head);
        if (ans == null) System.out.println("没有环，入环节点为null");
        else System.out.println(ans.value);

        System.out.println("------------");
        //测试是否有入环节点，笔试，面试不一样
        Node head2 = createLinkNode1();
        Node ans2 = getLoopNodePen(head);
        if (ans2 == null) System.out.println("没有环，入环节点为null");
        else System.out.println(ans2.value);
    }


    public static void main(String[] args) {
        test();
    }

不管笔试还是面试的代码，都能过：

2
------------
2

---

四、给你2个链表和他们的入环节点，如果其中一个有环，而另一个没有环，求相交点

上面，给了2个链表，可以单独求每一个链表的入环节点：

Node loop1 = getLoopNodeFace(head1);
Node loop2 = getLoopNodeFace(head2);

好，咱现有既有链表，也有了他们的入环节点（虽然可能是null哦）

我们就来分四种情况：
（1）loop1 == null && loop2 == null 俩都无环
（2）if(loop1 != null && loop2 == null) 或者：if(loop1 == null && loop2 != null) 其中一个有环，有一个无环
（3）if(loop1 != null && loop2 != null) 俩都有环

鉴于其中一个有环，有一个无环很特殊，非常简单，咱们先把这个求了，故本节的标题立为四
咱们把上面的情况（1）放到三，但是下面一节，咱再说它

本节：四、给你2个链表和他们的入环节点，如果其中一个有环，而另一个没有环，求相交点
情况（2）if(loop1 != null && loop2 == null) 或者：if(loop1 == null && loop2 != null) 其中一个有环，有一个无环
即给你的2个链表中，其中一个有环，而另一个无环
其中一个无环，则不可能相交，要是交了，另一个有环那个环也必然是无环链表上的环，岂不矛盾了。

因为单链表只有一个next指针，它只能去一个环，绝对不会分身去第二个支路
下面这种情况是不可能的：

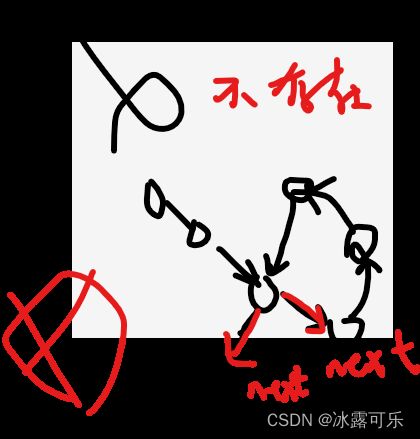
所以两条链表，只要是一个有环，一个没环，不可能相交，交点就是null。
这很简单吧，代码中直接返回null。

下面几个大情况，就比较复杂了

---

三、给你2个链表和他们的入环节点，如果都没有环，求相交点

情况（1）loop1 == null && loop2 == null 俩都无环
即2个链表都无环
又分为2种情况

1）俩都无交点，平行的

这种情况，怎么求交点呢？很好办
（1）让cur1走head1，cur2走head2
（2）如果走完之后，发现，cur1 ！= cur2，何谈相交呢？
对吧，既然不相等，那就是返回null作为交点。

2）俩相交了，最后汇聚到一条链上。

这种情况该怎么求交点呢？
这么做，挺6的
（1）让cur1走head1，cur2走head2
（2）如果走完之后，发现，cur1 = cur2，显然就是相交的
如何确定相交的交点呢？
（3）如果长的那根链表长度为n1，短的那根链表长度为n2，因为末端都是相同的，则必然
n1-n2就是交点之前，head1比head2多出来的长度
故，让cur从新从head1走n1-n2，再让head2和head1同步走，必定同时走到交点处。

这个过程很有趣，自己画图理解一下

n1=100，n2=80，末端相同的地方有60，则n1还有40在头，n2有20在头，自然n1在交点前，要多出20【n1-n2】
所以让n1先走就是对的

这个过程，在代码实现过程中，很有特点！！
【具体咋实现呢？
不是让cur1和cur2去记各自长度，
（1）而是先让cur1走，记n为cur1的长度
（2）然后让cur2，让n–，把短链cur2的长度抵消
剩下的n就是n1-n2的差值了
（3）我们默认cur1就是长链，所以要把长链交给cur1，短链交给cur2
（4）让cur1多走n步，随后与cur2同步走
（5）cur1和cur2必定在交点处相遇】

//给你2个链表和他们的入环节点，如果都没有环，求相交点
    //（1）让cur1走head1，cur2走head2
    //（2）如果走完之后，发现，cur1 = cur2，显然就是相交的
    //如何确定相交的交点呢？
    //（3）如果长的那根链表长度为n1，短的那根链表长度为n2，因为末端都是相同的，则必然
    //n1-n2就是交点之前，head1比head2多出来的长度
    //故，让cur从新从head1走n1-n2，再让head2和head1同步走，必定同时走到交点处。
    public static Node noLoopNodeGetCross(Node head1, Node head2){
        //既然没有环，那也不会有入环节点，就不用串loo1和loop2了
        if (head1 == null || head2 == null) return null;//压根没有第二条链表

        //用n来模拟长链和断链长度的差
        int n = 0;
        //（1）让cur1走head1，cur2走head2
        Node cur1 = head1;
        Node cur2 = head2;
        while (cur1 != null) {
            n++;//计数长度
            cur1 = cur1.next;
        }
        while (cur2 != null) {
            n--;//head2走就要--，最后n就是长短只差
            cur2 = cur2.next;
        }
        //（2）如果走完之后，发现，cur1 = cur2，显然就是相交的
        if (cur1 != cur2) return null;//两个链表平行，不想交

        //否则就是相交的
        //咱需要把长链给cur1，短链给cur2
        cur1 = n >= 0 ? head1 : head2;
        cur2 = cur1 == head1 ? head2 : head1;
        //然后差值将其正数画，现在长链已经在cur1上，n必须>0
        //让长链走线n，弥补差值
        n = n < 0 ? -n : n;
        while (n != 0){
            n--;
            cur1 = cur1.next;
        }
        //然后cur1和cur2同步走
        while (cur1 != cur2){
            cur1 = cur1.next;
            cur2 = cur2.next;
        }
        //一旦相遇，就是交点。

        return cur1;
    }

测试一下：

//造2根链表，然后相交与1个点,2个都无环，返回head1, head2
    public static Node[] create2LinkNode(){
        Node head1 = new Node(1);
        Node n2 = new Node(2);
        Node n3 = new Node(3);
        Node n4 = new Node(4);
        Node n5 = new Node(5);//1-2-3-4-5
        head1.next = n2;
        n2.next = n3;
        n3.next = n4;
        n4.next = n5;

        Node head2 = new Node(6);//让它直接去交head1的3节点
        head2.next = n3;

        return new Node[] {head1, head2};
    }
    public static void test2(){
        Node[] head = create2LinkNode();
        Node head1 = head[0];
        Node head2 = head[1];

        Node ans = noLoopNodeGetCross(head1, head2);
        if (ans == null) System.out.println("无交点");
        else System.out.println("交点是："+ ans.value);

    }
       public static void main(String[] args) {
//        test();
        test2();
    }

结果相交与点3：交点是：3

---

五、给你2个链表和他们的入环节点，如果都有环，求相交交点

好，现在是最后一种大情况：
（3）if(loop1 != null && loop2 != null) 俩都有环
两个链表都有环，链表1的入环节点为loop1，链表2的入环节点为loop2
咱们如何求这俩链表的交点呢？？？

又分为以下三种小情况：
1）俩的环是独立的，压根不相交；
2）两个相交，而且入环节点是同一个；
3）2个链表相交，但是入环节点不相同；
可以看下下面的案例

两个环没有交点

1）俩的环是独立的，压根不相交

两个环交点是同一个点

2）两个相交，而且入环节点是同一个，也是交点

还有这样的情况：h1和h2先交了，入环节点不是交点

两个环的交点是不同的2个点

3）2个链表相交，但是入环节点不相同。交点可以是loop1，也可以是loop2

发现啥了么？
我们看看loop1和loop2是否相等？？

——上面的1）和3）
1）俩的环是独立的，压根不相交；
3）2个链表相交，但是入环节点不相同；
不管交还是不交，loop1都不等于loop2,

求交点怎么求呢？？？咱们可以这么看1）3）
设定cur1，让他们从loop1.next开始走，如果最后cur1竟然与loop2相遇，说明一定是相交的，交点也就是loop1或者loop2，随意
如果cur1回到loop1了，一直没有遇到loop2，说明压根不相交。
你瞅瞅图，看看是不是

——我们在看上面的2）
可能提前交，也就是交点，不是入环节点（loop1或者loop2）
也可能交点就是其中一个入环节点
怎么求？？
你回去上面看一下：
三、给你2个链表和他们的入环节点，如果都没有环，求相交点，中的情况2）
看红色两条链表，尾部是null

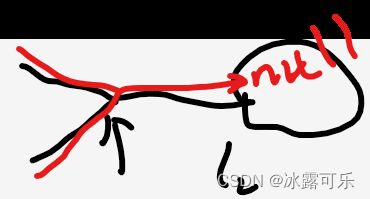
无非，这里的链表时两个相交，而且入环节点是同一个；
尾部不是null而是一个环，null被换成了loop1=loop2

所以，三、给你2个链表和他们的入环节点，如果都没有环，求相交点，中的情况2）的求法中，代码，直接改一下，
就是这个小情况的代码

以上这所有的三种小情况，综合一下代码就是：

//给你2个链表和他们的入环节点，如果都有环，求相交交点
    //又分为以下三种小情况：
    //1）俩的环是独立的，压根不相交；
    //2）两个相交，而且入环节点是同一个；
    //3）2个链表相交，但是入环节点不相同；
    public static Node bothHasLoopCross(Node head1, Node head2,
                                        Node loop1, Node loop2){
        //俩交于1一个点，提前交，或者直接在入环节点loop1=loop2那交
        //2）两个相交，而且入环节点是同一个；
        if (loop1 == loop2){
            //用n来模拟长链和断链长度的差
            int n = 0;
            //（1）让cur1走head1，cur2走head2
            Node cur1 = head1;
            Node cur2 = head2;
            while (cur1 != loop1) {//从null替换为loop1
                n++;//计数长度
                cur1 = cur1.next;
            }
            while (cur2 != loop1) {//从null替换为loop1
                n--;//head2走就要--，最后n就是长短只差
                cur2 = cur2.next;
            }
            //（2）如果走完之后，发现，cur1 = cur2，显然就是相交的
            if (cur1 != cur2) return null;//两个链表平行，不相交

            //否则就是相交的
            //咱需要把长链给cur1，短链给cur2
            cur1 = n >= 0 ? head1 : head2;
            cur2 = cur1 == head1 ? head2 : head1;
            //然后差值将其正数画，现在长链已经在cur1上，n必须>0
            //让长链走线n，弥补差值
            n = n < 0 ? -n : n;
            while (n != 0){
                n--;
                cur1 = cur1.next;
            }
            //然后cur1和cur2同步走
            while (cur1 != cur2){
                cur1 = cur1.next;
                cur2 = cur2.next;
            }
            //一旦相遇，就是交点。不论是交在前面，还是刚刚好交在loop1=loop2处，都是cur1
            return cur1;
        }else {
            //1）俩的环是独立的，压根不相交；
            //3）2个链表相交，但是入环节点不相同；
            //求交点怎么求呢？？？咱们可以这么看1）3）
            //设定cur1，让他们从loop1.next开始走，如果最后cur1竟然与loop2相遇，说明一定是相交的，交点也就是loop1或者loop2，随意
            //如果cur1回到loop1了，一直没有遇到loop2，说明压根不相交。
            Node cur1 = loop1.next;
            while (cur1 != loop1){
                if (cur1 == loop2) return loop2;//3）2个链表相交，但是入环节点不相同；现在找到了交点，任选其一
                cur1 = cur1.next;
            }
            //1）俩的环是独立的，压根不相交；
            return null;
        }
    }

测试一把：
有环，刚刚好交在同一节点3那：

//造2根链表，然后相交与1个点,2个都有环，返回head1, head2
    public static Node[] create2LinkNodeHasCross(){
        Node head1 = new Node(1);
        Node n2 = new Node(2);
        Node n3 = new Node(3);
        Node n4 = new Node(4);
        Node n5 = new Node(5);//1-2-3-4-5，然后咱，让n5指向n3，做环
        head1.next = n2;
        n2.next = n3;
        n3.next = n4;
        n4.next = n5;
        n5.next = n3;

        Node head2 = new Node(6);//让它直接去交head1的3节点
        head2.next = n3;

        return new Node[] {head1, head2};
    }
    public static void test3(){
        Node[] head = create2LinkNode();
        Node head1 = head[0];
        Node head2 = head[1];
        //独立获取入环节点
        Node loop1 = getLoopNodeFace(head1);
        Node loop2 = getLoopNodeFace(head2);
        //看看是否有交点？
        Node ans = bothHasLoopCross(head1, head2, loop1, loop2);
        if (ans == null) System.out.println("无交点");
        else System.out.println("交点是："+ ans.value);

    }

    public static void main(String[] args) {
//        test();
//        test2();
        test3();
    }

再测试一把：如果有环，但是不交呢？

//造2根链表，然后相交与1个点,2个都有环，返回head1, head2
    public static Node[] create2LinkNodeHasCross2(){
        Node head1 = new Node(1);
        Node n2 = new Node(2);
        Node n3 = new Node(3);
        Node n4 = new Node(4);
        Node n5 = new Node(5);//1-2-3-4-5，然后咱，让n5指向n3，做环
        head1.next = n2;
        n2.next = n3;
        n3.next = n4;
        n4.next = n5;
        n5.next = n3;

        Node head2 = new Node(6);
        Node n7 = new Node(7);
        Node n8 = new Node(8);
        head2.next = n7;
        n7.next = n8;
        n8.next = head2;//整体一个环，但是与head1没有交集

        return new Node[] {head1, head2};
    }

    public static void test3(){
        Node[] head = create2LinkNodeHasCross();
        Node head1 = head[0];
        Node head2 = head[1];
        //独立获取入环节点
        Node loop1 = getLoopNodeFace(head1);
        Node loop2 = getLoopNodeFace(head2);
        //看看是否有交点？
        Node ans = bothHasLoopCross(head1, head2, loop1, loop2);
        if (ans == null) System.out.println("无交点");
        else System.out.println("交点是："+ ans.value);

        System.out.println("----------");
        head = create2LinkNodeHasCross2();//不交
        head1 = head[0];
        head2 = head[1];
        //独立获取入环节点
        loop1 = getLoopNodeFace(head1);
        loop2 = getLoopNodeFace(head2);
        //看看是否有交点？
        ans = bothHasLoopCross(head1, head2, loop1, loop2);
        if (ans == null) System.out.println("无交点");
        else System.out.println("交点是："+ ans.value);
    }

    public static void main(String[] args) {
//        test();
//        test2();
        test3();
    }

两个测试都没问题：

交点是：3
----------
无交点

---

链表噩梦题之一：2条链表相交问题，链表可能有环，也可能无环，求交点

根据上面的表述，我们需要做以下几个步骤：
（1）上面，给了2个链表，可以单独求每一个链表的入环节点：

Node loop1 = getLoopNodeFace(head1);
Node loop2 = getLoopNodeFace(head2);

好，咱现有既有链表，也有了他们的入环节点（虽然可能是null哦）

我们就来分四种情况：
（1）loop1 == null && loop2 == null 俩都无环，求相交点
（2）if(loop1 != null && loop2 == null) 或者：if(loop1 == null && loop2 != null) 其中一个有环，有一个无环，求相交点
（3）if(loop1 != null && loop2 != null) 俩都有环，求相交点

综合，解决了链表噩梦题之一：链表相交问题，求交点

//综合：链表噩梦题之一：2条链表相交问题，链表可能有环，也可能无环，求交点
    public static Node nightMireCrossNode(Node head1, Node head2){
        if (head1 == null || head2 == null) return null;

        Node loop1 = getLoopNodeFace(head1);
        Node loop2 = getLoopNodeFace(head2);

        //（1）`loop1 == null && loop2 == null` 俩都无环，求相交点
        if (loop1 == null && loop2 == null) return noLoopNodeGetCross(head1, head2);
        //（2）`if(loop1 != null && loop2 == null)`
        // 或者：`if(loop1 == null && loop2 != null)`
        // 其中一个有环，有一个无环，求相交点
        else if (loop1 != null && loop2 != null) return bothHasLoopCross(head1, head2, loop1, loop2);
        //（3）`if(loop1 != null && loop2 != null)` 俩都有环，求相交点
        else return null;//压根没有的
    }

这些代码，就是一个综合的情况，实际上就是综合了上面五道大题！！！这学过了，怎么也不会在面试场上怯场了！！

---

总结

提示：重要经验：

1）链表噩梦题有2个：第一个就是本题，链表的交点问题，第二个就是约瑟夫环问题，找活下来那个人最初的编号。
2）链表问题，最重要的搞懂核心思想，然后coding清楚，快慢指针要了解。
3）笔试求AC，可以不考虑空间复杂度，但是面试既要考虑时间复杂度最优，也要考虑空间复杂度最优。