4.2学习周报
文章目录
- 前言
- 文献阅读
-
- 摘要
- 介绍
- 时间序列预测目前存在的问题
- 时间序列预测方法分类
- 未来方向
- 时间序列预测
- 总结
前言
本周阅读文献《Forecast Methods for Time Series Data: A Survey》,本文主要对目前时间序列数据建模方法进行分类,主要分为了三类:经典的时序预测方法、机器学习的时序预测模型以及将经典方法和机器学习相结合的混合模型,对不同的方法进行比较;指出时间序列预测的潜在研究方向,主要是三个方面,在数据上可以进行数据预处理提高数据质量,在模型方面对模型进行修正以提高预测能力以及提高并行计算的效率。另外,在阅读文献时了解了一种预测模型叫高斯过程回归,对这个方法进行了初步的学习。
This week,I read an article which attempts to cover the existing modeling methods for time series data and classify them.The existing popular prediction methods of time series are classified into three categories: classical forecasting method of time series, prediction methods of machine learning and deep learning, and hybrid forecasting methods of time series.In addition, we make comparisons between different methods and summarize several potential research directions and unsolved problems, such as data preprocessing, incremental data model construction, and parallel computing.In addition, I learn about a prediction model called Gauss process regression .
文献阅读
题目:Forecast Methods for Time Series Data: A Survey
作者:Liu, ZY (Liu, Zhenyu) [1] ; Zhu, ZT (Zhu, Zhengtong) [1] ; Gao, J (Gao, Jing) [1] ; Xu, C (Xu, Cheng) [1]
文献链接
摘要
时间序列数据预测方法研究成为热点之一。越来越多的时间序列数据在各个领域产生。为时间序列分析方法的研究提供数据,促进时间序列研究的发展。由于时间序列数据的生成高度复杂、规模大,时间序列数据预测模型的构建带来了更大的挑战。时间序列建模面临的主要挑战是时间序列数据复杂度高、预测模型准确率低、泛化能力差。本文试图对现有的时间序列数据建模方法进行分类。此外,我们还对不同的方法进行了比较,并列出了一些时间序列预测的潜在方向。
介绍
时间序列数据是指在等间隔的时间段内,以给定的采样率观测某一过程的结果。时间序列分析的核心是从数据中发现规律,并根据历史观测预测未来值,可以为决策提供参考和依据。传统的基于概率和统计的时间序列预测方法在气象、金融、工业等领域取得了巨大的成果。然而,随着大数据时代的发展,海量的、服从多种分布模式的非线性时间序列数据正在不断产生,这也对时间序列预测方法提出了更高的挑战。因此,人们应用机器学习和深度学习对高度复杂的时间序列数据预测方法,并取得了很大的成果。
时间序列预测目前存在的问题
- 在数据方面:数据分析和建模的准确性受到数据质量的严重影响。因此,数据的质量在数据分析中起着决定性的作用。然而,在现实中,原始数据并不完美。一方面,时间序列数据由传感器、智能终端设备、采集系统等实验仪器等生成。由于客观条件和数据采集设备的稳定性等各种因素,数据往往含有噪声、缺失值等异常情况。如何基于样本数据的分布模式处理异常值和缺失值,这对大规模时间序列数据预处理方法提出了更高的挑战。
- 在模型方面:目前,研究人员通常根据历史数据构建预测模型,以对未来数据进行预测分析。然而,在实际应用中发现,随着时间的推移,预测模型的精度和性能逐渐下降。主要原因是历史数据和实时数据之间的差距。而且新的数据特征并没有被模型增量学习并应用到预测中。
综上所述,基于在线增量数据的时间序列预测修正模型的研究已经成为一个亟待解决的问题。 - 在实时计算方面:由于各领域时间序列数据的快速增长,在线时间序列实时分析已经成为发展需求。
实时计算。由于各领域时间序列数据的快速增长和对数据时效性的需求,对时间序列数据进行在线实时分析成为发展需求。现在的时间序列分析模型通常采用单机模式。通过使用高性能的GPU服务器,提高了运行效率。一方面,GPU服务器价格昂贵,导致研发成本较高;另一方面,受计算资源和数据规模的影响,无法实现实时计算。
时间序列预测方法分类
根据时间序列预测方法的发展历程,我们将现有流行的时间序列预测方法分为三大类:经典的时间序列预测方法、机器学习和深度学习的预测方法以及时间序列的混合预测方法。
A. 时间序列的经典预测方法
时间序列的经典预测方法基于数学和统计建模,经典线性模型主要包括:自回归(AR)模型、移动平均(MA)模型、自回归移动平均(ARMA)模型和自回归积分移动平均(ARIMA)模型。而经典的非线性线性模型主要包括阈值自回归(TAR)模型,恒定条件相关(CCC)模型、条件异方差性模型。此外,还有一些基于指数平滑的重要经典预测方法,如:简单指数平滑(SES)、霍尔特线性趋势法、霍尔特-温特斯乘法、霍尔特-温特斯加法和霍尔特-温特斯阻尼法。
1)经典线性模型
a:针对平稳数据的预测模型
对于平稳时间序列的预测,Yule[4]首先将随机性的概念引入时间序列,将每个时间序列视为随机过程的实现,并提出了自回归(AR)模型,将每个时间序列视为随机过程的实现,并提出了AR模型。然后,研究人员提出了移动平均(MA)模型,并提出了著名的将分解定理[5]。为时间序列预测的研究奠定了基础。直到1970年,Box和JenKins提出了ARMA模型[6],其中包括三个基本模型:AR模型,MA模型和ARMA模型。它广泛用于平稳时间序列的建模。
ARMA 模型是预测稳态时间序列数据的最常见模型。它将时间序列数据视为一个随机序列,这些随机变量的依赖性反映了原始数据在时间上的连续性。

随着格兰杰因果关系[12]的提出,研究人员将单变量时间序列模型扩展到多变量时间序列分析。基于ARMA模型,提出了一种面向量自回归移动平均线(VARMA)的多元促进模型,可以灵活地表示向量自回归(VAR)和向量移动平均(VMA)模型。构建 VARMA 模型时,时间序列数据必须是平稳序列。如果数据是非平稳时间序列,则需要进行一阶差分处理才能获得平稳数据。但是,在差分处理中将忽略时间序列中存在的趋势信息。为了解决上述问题,恩格尔和格兰杰[13]提出了向量纠错模型(VECM),该模型可以很好地考虑时间序列之间的协整关系。
综上所述,ARMA时间序列预测模型在平稳时间序列预测方面取得了很大成就。但是,实时序列数据中几乎没有纯粹的平稳数据。因此,该模型的应用受到数据特性的限制,其通用性较差。
b:非平稳数据的预测模型
包含趋势、季节性或周期性等特征的序列称为非平稳序列。它可能只包含一个组件或多个组件。非平稳时间序列意味着在其局部水平或趋势消除后,它显示出同质性。此时,该系列的某些部分与其他部分非常相似。这种非平稳时间序列可以在差分处理后转换为平稳时间序列。
ARIMA(p, d, q)是一种众所周知的非平稳时间序列模型,可以反映不同数据模式的变化,并且模型需要较少的参数来估计。因此,ARIMA模型得到了广泛的应用。

ARIMA的模型结构简单。应用ARIMA模型时,要求时间序列数据是平稳的,或者经过微分后的稳定。因此,ARIMA 只能捕获线性关系,而不能捕获非线性关系。
2) 经典非线性模型
线性预测模型易于理解且易于实现。然而,线性模型需要线性假设下构建,这对于非线性时间序列数据效果较差。为此,提出了非线性时间序列预测模型。著名的经典非线性模型包括阈值自回归(TAR)模型、自回归条件异方差(ARCH)模型和恒定条件相关(CCC)模型等。
B.时间序列的机器学习预测模型
经典的时间序列预测模型可以很好地捕捉时间序列中的线性关系,并在数据集较小时取得良好的效果。然而,当应用于大规模复杂非线性时间序列时,效果较差。因此,研究人员更加关注机器学习或深度学习的时间序列预测方法。多层感知器(MLP)网络[36]和径向基函数(RBF)网络[37]等人工神经网络具有自适应和自组织学习机制。它们是不同领域最早用于非线性时间序列预测的神经网络模型,并且取得了良好的效果。此外,模糊理论、高斯过程回归、决策树、支持向量机、LSTM 等。也用于时间序列预测,对非线性时间序列也有很好的预测能力。
1)模糊时间序列预测方法
模糊时间序列预测可以解决非线性问题,是预测分析领域的研究热点之一。常用于小数据集或有缺失值的数据集的时间序列预测。
2) 人工神经网络
人工神经网络 (ANN) 是一种数据驱动的预测模型。具有较强的自组织、自学习和良好的非线性逼近能力。因此,它引起了时间序列预测领域研究人员的广泛关注。它已成为非线性建模的有效工具之一,并广泛用于各个领域。在ANN模型中,假设训练样本的数量趋于无限,但实际训练样本是有限的。因此,训练模型往往存在过拟合现象,特别是在小样本建模中,模型的性能劣化更为明显。虽然人工神经网络在时间序列预测方面取得了不错的效果。但是,在数据尺度的影响下,经常发生过拟合。因此,人工神经网络不适合小数据样本的时间序列预测。混合模型在预测方面优于单一模型。研究表明,混合模型在预测方面比单一模型表现更好。
3) 高斯过程回归
高斯过程(GP)[67]是一种基于贝叶斯神经网络的机器学习方法。它是一组随机变量。集合中任意数量的随机变量服从联合高斯分布,并由均值函数和协方差函数唯一确定。
高斯过程回归 (GPR) [68] 是一种非参数模型,它使用高斯过程 (GP) 先验对数据执行回归分析。GPR的模型假设包括噪声(回归残差)和高斯过程先验。它是根据贝叶斯推理[69]求解的。GPR是紧凑空间中任何连续函数的通用近似器。此外,GPR可以提供后验来预测结果。当可能性呈正态分布时,后验具有分析形式。因此,GPR是一种具有多功能性和可解析性的概率模型。
高斯过程回归(GPR)是一种贝叶斯机器学习方法。由于GPR的计算成本高,通常用于低维和小样本回归问题。同时,与ANN和SVM等方法相比,GPR需要更少的建模参数和更多的内核函数,因此GPR更加灵活。
4) 支持向量机
支持向量机(SVM)是Vapnik团队[83]首先提出的一种重要的分类算法,对于小样本和非线性问题具有独特的优势。它广泛用于分类、模式识别和时间序列预测的研究。支持向量机最初应用于二维线性可分情况。核心思想是在分类精度的基础上找到最优的超平面。支持向量机的主要优点是数据分类。在分类方面,适用于小样本数据集,简化了分类和回归问题。它的计算复杂度由支持向量的数量决定,从而避免了“维数的诅咒”。此外,其结果由几个支持向量决定。它对异常值不敏感,因此可以很好地捕获关键样本,具有良好的鲁棒性和泛化能力。但在预测方面,单一支持向量机模型效果不佳,通常采用混合模型进行预测,可以达到一定的效果。
5) 递归神经网络
递归神经网络(RNN)以序列数据为输入,递归地沿序列的进化方向,所有节点连接在链中。擅长处理序列和相关数据,广泛应用于模式识别和时间序列预测领域。RNN对时间序列更敏感,并且在数据传输中具有内存。
然而,输入序列越长,需要的时序参考就越多,从而导致网络更深。当序列较长时,梯度很难从后一个序列传播回前一个序列。结果,出现了梯度消失的问题,因此不可能处理长期依赖的问题。为了解决RNN梯度消失和爆炸的问题,提出了一种长短期记忆(LSTM)模型。它是一种特殊的RNN,通过在输入和反馈之间产生“保留效应”,有效地避免了梯度分散的现象。与 RNN 的叠加记忆相比,LSTM 可以记住需要长时间记忆的信息,忘记不重要的信息。因此,LSTM在长序列预测中具有更好的性能。
6) Transformer
Transformer 是 Google 团队在 2017 年提出的经典 NLP 模型。流行的伯特模型也是基于变形金刚的。Transformer 模型使用自我注意机制而不是 RNN 的顺序结构,因此可以并行训练模型并获取全局信息。它目前也用于时间序列预测。
Transformer用于时间序列预测,并取得了良好的效果。它可以很好地捕获时间序列之间的复杂依赖关系,并且可以并行计算。但是,该方法变换器无法捕获序列之间的远距离信息,并且计算量较大。
C.混合预测模型
在时间序列预测领域,经典和机器学习的预测方法各有优势。然而,实时时间序列数据具有以下特点:(1)难以判断时间序列数据是线性还是非线性,无法判断某一特定模型对数据的有效性;(2)现实中,纯线性或纯非线性的时间序列数据很少,时间序列数据通常是线性和非线性的结合;(3)在时间序列预测领域,没有任何模型适用于任何情况,单一模型无法同时捕捉不同的时间序列模式。
因此,为了捕捉数据中不同的分布模式,将经典和机器学习相结合的混合模型成为发展趋势。混合模型可以捕捉时间序列复杂的分布模式,提高模型的准确性和泛化能力。
1)基于ARMA和机器学习的混合模型
ARMA与机器学习相结合的混合算法已应用于不同领域,并取得了良好的效果。
2)基于ARIMA和机器学习的混合模型
3)基于机器学习的混合模型
比如有文献提出了一种混合时间预测模型,该模型结合了卷积神经网络(CNN)和支持向量机(SVM)。
未来方向
数据预处理
众所周知,数据的质量对数据建模有着重要的影响。但是,在生成海量时间序列数据的过程中,存在一些缺失的数据。目前,还没有找到一种高精度、高效率的填充时间序列缺失值的方法。然而,随着时间序列数据分析的需要,我们认为基于原始数据分布模式填充缺失值将成为时间序列分析研究领域非常有前途的方向。
模型构建
将实时增量数据的特点与模型相结合,提高模型的准确性和鲁棒性。目前,人们通常根据历史时间序列数据构建预测模型,并将其用于未来的数据预测。然而,随着时间的流逝和各种客观因素的影响,需要根据新数据的特点和数据分布模式对模型进行修正,以提高其准确性和鲁棒性。否则,随着时间的推移,模型的预测精度和性能将无法满足我们的需求。因此,基于增量数据的修正时间序列预测模型将成为潜在的研究方向。
并行计算
目前,时间序列分析模型是基于单机模式构建的。研究人员通常使用高性能GPU服务器来提高计算效率。一方面,GPU服务器设备昂贵,增加了研究成本。另一方面,受计算资源和数据规模的影响,无法实现实时预测分析。因此,基于大数据技术的时间序列数据并行计算将成为潜在的研究方向。
时间序列预测
上面的文献中提到了一种机器学习预测模型的方法是高斯过程回归,下面对高斯过程回归预测进行初步学习和了解。
时间序列的机器学习预测模型:高斯过程回归
高斯过程是一种常用的监督学习方法,可以用于解决回归和分类问题。高斯过程回归预测也就是我们要用高斯过程来进行回归并预测。高斯过程模型的优势主要体现在处理非线性和小数据问题上。
基础知识
一维高斯分布(也就是正态分布)的概率密度函数决定因素有两个:均值和方差 (标准差)。因此我们可以得到一个结论:一个均值和一个方差可以确定一个一维的高斯分布!

二维高斯分布的概率密度函数如下,我们将这幅图分别从XOZ和YOZ两个方向看,我们可以看到两个方向得到的截面完全遵循一维高斯分布,那么有两个一维高斯分布是不是需要两个均值和方差来确定,那么也就是说,两个均值和两个方差可以确定一个二维高斯分布,不妨把这个假设扩展到n维。
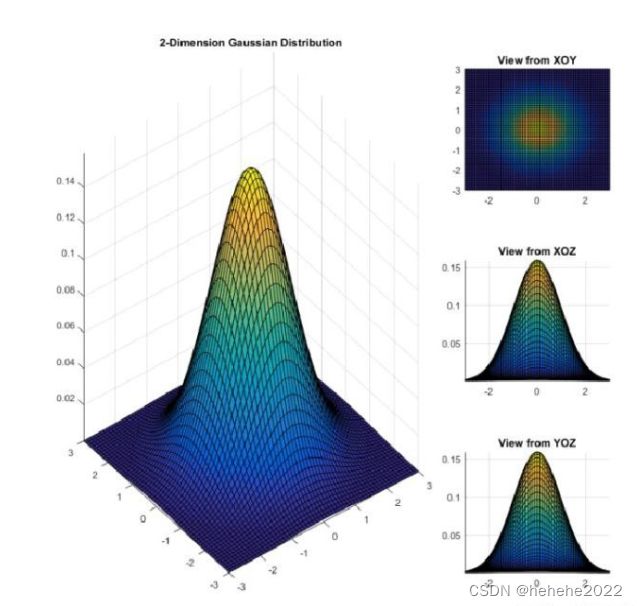
得出:n维高斯分布的表达式,对比一维高斯分布进行理解。

引入协方差的概念,在多维的高斯分布当中,两两分布之间肯定存在某种联系,这种关系是通过矩阵进行表达的。矩阵那么多元素,是可以将每个元素代表两个东西之间的某种关系,n维的高斯分布需要n个均值和n个方差来确定,通常情况下我们将均值定为一个均值向量,方差组用一个矩阵来表示——协方差矩阵,当两两分布之间相互独立,则这个协方差矩阵为对角矩阵,反之为非对角矩阵。一个均值和一个方差能确定一个一维的高斯分布,那么多维的高斯分布就可以通过一个均值向量和一个协方差矩阵确定。

高斯过程
高斯过程:“如果多元高斯分布的随机变量为无数个,且是离散时间的状态量,即随机变量为随时间变化的函数。其中每个时刻的均值用一个均值函数刻画,两个不同时刻的方差用一个协方差函数刻画。”理解这句话,将多维高斯分布的维数放大到无限大,其中均值向量里的每个元素都遵循一个函数——均值函数,就是说你给我这个无限维的高斯分布中某一维的高斯分布,我可以根据均值函数给出这一维高斯分布的均值。那么同理我们设置一个协方差函数,这个协方差函数可以根据需要而给出对应的协方差矩阵。一个高斯过程可以由一个均值函数和一个协方差函数来确定!

协方差函数又称为核函数,左下角是一个协方差函数,这个函数是经典的高斯核函数,一个协方差函数确定一个协方差矩阵如右下角。

把无限维的高斯分布,每一维按时间线或者其他量展开,就得到一个高斯分布的曲线,这个曲线中的每一个点都对应了一个一维的高斯分布,而每个高斯分布都有一个均值和方差,故高斯过程中每个点对应一个均值和方差。
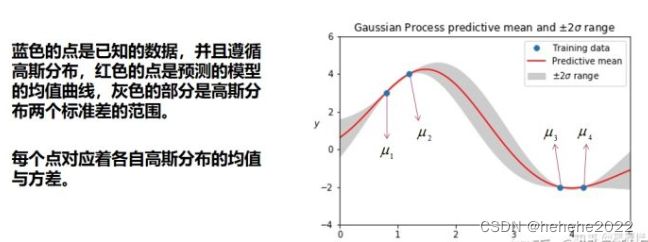
高斯过程怎么来做预测?

第一步,确定数据点为一个高斯过程的采样点。要确定这些孤立的点是遵循一个高斯过程的,但是高斯过程又是由一个均值函数和一个协方差函数来确定的,也就是说我们要找均值函数和协方差函数,这里我们不妨设均值函数为常数0,也就是每个点对应的高斯分布的均值为0!那么协方差函数怎么确定呢?我们采用一个经典的高斯核函数的变形来确定这个高斯过程的协方差函数,函数表达式中有没法确定的未知量,我们称之为超参数。知道了高斯过程的均值函数和协方差函数,通过贝叶斯推断求出了所要求的点条件概率均值和方差的表达式。超参数通过最大似然估计求解。
参考:https://blog.csdn.net/qq_50310065/article/details/111775468
总结
对不同时间序列模型进行了比较分析。每个模型的数据特性、优点和缺点分别汇总:

使用GPR方法进行时序预测的文献:
1.Multistep ahead groundwater level time-series forecasting using Gaussian process regression and ANFIS
2.Uncertain prediction for slope displacement time-series using Gaussian process machine learning
3.Gaussian process regression for forecasting battery state of health
4.Monthly streamflow forecasting using Gaussian process regression