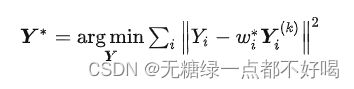2023.03.19 学习周报

---

摘要

This week, I read a computer science related to sequential recommendation systems; Due to existing recommendation systems embedding user history behavior records into a potential vector/representation, it may lose the correlation between user history and future interests; In response, this computer science proposes a new memory based recommendation algorithm, which can effectively integrate the user’s historical behavior records into the recommendation system; Finally, experimental analysis on multiple actual data sets shows that this method can extract intuitive patterns of users’ impact on future behavior. In addition, I learn the LLE algorithm, LLE can learn the overall structure of nonlinear manifolds, it can map inputs from high dimensional spaces to low dimensional spaces, and this optimization does not affect local minima and correlations within the data.

本周，我阅读了一篇与顺序推荐系统相关的文章；由于现有的推荐系统将用户历史行为记录嵌入到一个潜在的向量/表示中，这可能会失去了用户历史记录和未来兴趣之间的相关性；对此，文章提出了一种新的基于记忆的推荐算法，该算法可以有效地将用户的历史行为记录整合到推荐系统中；最后，通过在多个实际数据集上实验分析表明，该方法能够提取用户对未来行为影响的直觉模式。此外，我学习了LLE算法，LLE能学习非线性流形的整体结构，它能将高维空间的输入映射到低维空间，并且此优化不会影响局部最小值和数据内部的相关性。

---

文献阅读

1.题目

文献链接：Sequential Recommendation with User Memory Networks

2.摘要

User preferences are usually dynamic in real-world recommender systems, and a user’s historical behavior records may not be equally important when predicting his/her future interests. Existing recommendation algorithms – including both shallow and deep approaches – usually embed a user’s historical records into a single latent vector/representation, which may have lost the per item- or feature-level correlations between a user’s historical records and future interests. In this paper, we aim to express, store, and manipulate users’ historical records in a more explicit, dynamic, and effective manner. To do so, we introduce the memory mechanism to recommender systems. Specifically, we design a memory-augmented neural network (MANN) integrated with the insights of collaborative filtering for recommendation. By leveraging the external memory matrix in MANN, we store and update users’ historical records explicitly, which enhances the expressiveness of the model. We further adapt our framework to both item- and feature-level versions, and design the corresponding memory reading/writing operations according to the nature of personalized recommendation scenarios. Compared with state-of-the-art methods that consider users’ sequential behavior for recommendation, e.g., sequential recommenders with recurrent neural networks (RNN) or Markov chains, our method achieves significantly and consistently better performance on four real-world datasets. Moreover, experimental analyses show that our method is able to extract the intuitive patterns of how users’ future actions are affected by previous behaviors.

3.介绍

现有方法的缺陷：
1）并不是所有的历史行为都对用户未来喜好有用；
2）现有的方法会将用户的历史序列用一个embedding进行表示，忽略了各个item之间的关系，以及各自的特征。

对此，论文的核心思想：
1）借助memory network显式利用用户历史行为记录增强模型表达能力；
2）利用注意力机制和记忆单元获得用户动态Embedding，以用于推荐新的item，这会增加模型的表达能力。

4.本文贡献

1）融合了协同过滤和记忆增强网络，使更加有效地使用用户历史记录；
2）提出两种item级别和feature级别的记忆网络，比较和研究了它们在topn推荐任务上的效果；
3）通过分析注意力机制，作者提供了一种检验解释：一个物品为什么会被模型推荐，以及用户历史行为是如何影响未来决策的。

5.RUM

Recommender system with external User Memory networks：

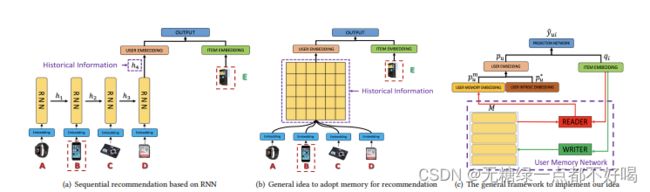
1）基于传统的RNN推荐，不区分的不同历史行为记录在当前一次推荐中的不同作用，仅利用固定的隐式因子或者隐态预测推荐；
2）每个用户使用外部记忆单元记忆历史行为，在预测时，动态注意力读出记忆作为用户Embeding表示，注意力机制衡量历史行为对当前物品推荐的重要性；
3）利用注意力分析用户行为的因果关系。

6.基本框架

6.1 Memory enhanced user embedding

用户个性化历史行为记忆矩阵Mu，用户记忆Embedding：pum， 综合Embedding：pu， 当前item Embedding：qi。

其中：MERGE的策略为elemet multiply、concat等，但效果在实验数据上不如weight vector add，权重参数可用于平衡记忆比重。

6.2 Prediction function

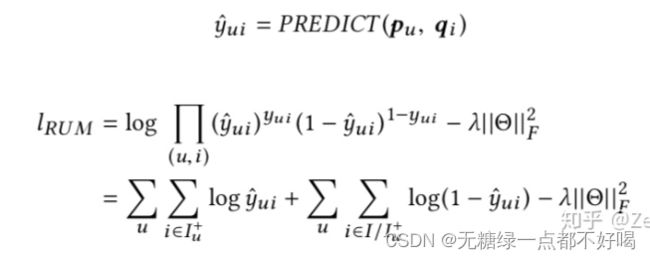
交叉熵损失函数 + Sigmoid（其他激活函数也可行），其中Iu+为正样本item集合，user即action list item rank in action timestamp。

Memory更新：根据采取action的item更新记忆

6.3 Item-level RUM

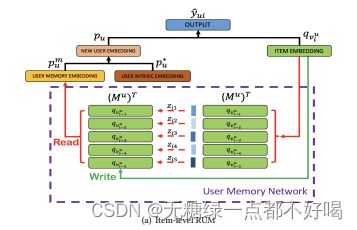
1）Reading operation
记忆矩阵Mu(D X k)，Item Embedding qviu(1 X D)，用户u正样本集合：{v1u,v2u,···,vu|Iu+|}，其中k为记忆槽数量：

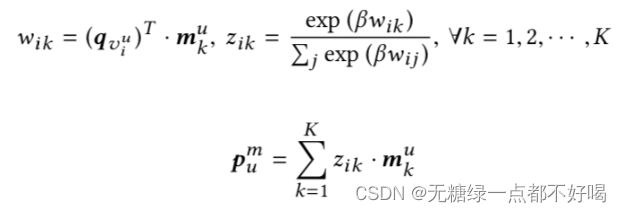
2）Writing operation
记忆矩阵Mu只存储最近的k个item，记忆矩阵是一个先进先出的队列，只保存最近k个item Embedding：

M写入前：

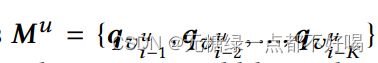
M写入后：

6.4 feature-level RUM

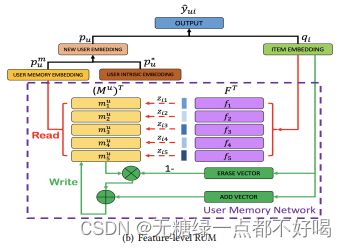
1）特定用户memory feature为Mu，全局latent feature F分为k个；
2）M Reading operation：

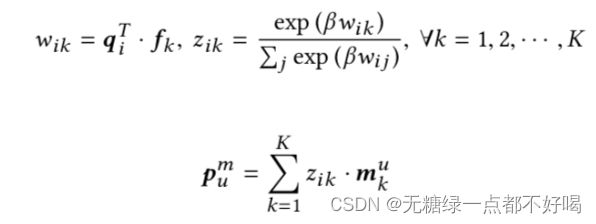
3）M Writing operation：

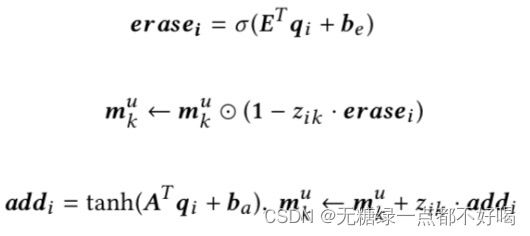
7.实验

7.1 数据集

实验在亚马逊数据集上进行，其中包含1996年5月至2014年7月期间亚马逊的用户产品购买行为；从四个产品类别进行评估，包括即时视频、乐器、汽车和婴儿护理四部分；为了提供顺序推荐，作者选择了至少有10次购买记录的用户进行实验：

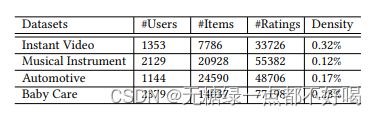
7.2 测量准则

1）Precision §, Recall ® and F1-score
为了更好地解释，作者采用了每个用户的平均值，而不是全局平均值：

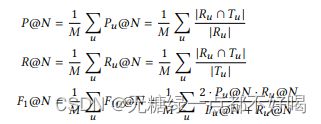
2）Hit-ratio (HR)
Hit-ratio给出了可以收到至少一个正确推荐的用户百分比，这在以前的工作中已经被广泛使用：

3）NDCG
归一化的累积增益，通过采取正确的位置来评估排名性能考虑的项目：

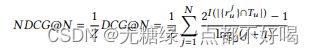
7.3 实验结果

1）记忆权重参数设置为0.2最佳，过大或过小都会导致效果变差；
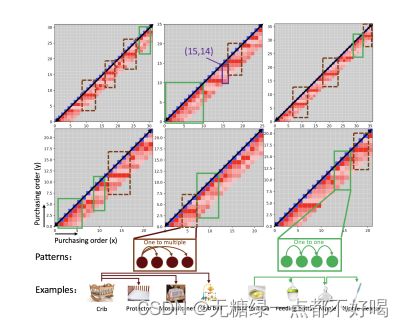
2）注意力解释历史行为影响模式：
模式一：用户行为被最近的上一次行为连续触发
模式二：一系列的行为被最近的某一次行为触发

8.总结

1、比较典型的基于用户历史信息的memory网络，增加了模型的拟合能力；
2、基于item的记忆框架跟DIN非常类似；
3、基于feature的记忆框架相当于在item级别上做了抽象，建模item抽象层的兴趣，DIEN建模item抽象层的兴趣变化；
4、Memory Embedding的几种使用方案：
1）单纯用user Embedding；
2）使用邻域user Embedding，注意力user协同；
3）使用action item list Embedding， 注意力item协同。

LLE

1.简介

LLE：局部线性嵌入，一种无监督的学习算法，用于计算高维输入的低维、邻域保护嵌入。与局部降维的聚类方法不同，LLE 将其输入映射到一个低维的全局坐标系中，并且其优化不影响局部极小值。利用线性重构的局部对称性，LLE 能够学习非线性流形的整体结构，如由人脸图像或文本文档生成的流形。

特点：
1）在 LLE 中，假设某个点xi坐标可以由它周围的一些点的坐标线性组合求出；
2）保持局部邻域几何结构，重构权重；
3）权重对样本集的几何变换具有不变性。

因此，我们可以发现 LLE 希望每个点与其邻近点的相对关系得以保持，但是 LLE 是从局部上考虑的。

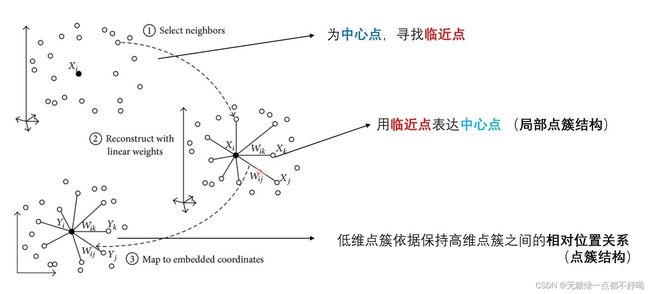
2.形象描述

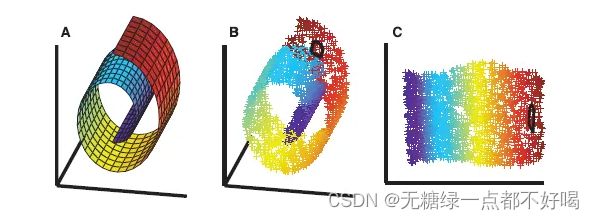
如上图所示，对于流形（A），我们可以通过采样得到三维数据（B）；再通过LLE算法可以将三维数据（B）映射到二维数据（C）；图中的颜色编码说明了由LLE发现的邻域保持映射；图（b）和（c）中的黑色轮廓表示单点的邻域。

3.步骤

前面提到LLE算法认为每一个数据点都可以由其近邻点的线性加权组合构造得到，即主要步骤分为以下三步：
1）寻找每个样本点的k个近邻点；
2）由每个样本点的近邻点计算出该样本点的局部重建权值矩阵；
3）由该样本点的局部重建权值矩阵和其近邻点计算出该样本点的输出值。

4.详细描述

既然希望样本点与邻近点的关系不变，我们自然就要将这种关系进行量化；具体来说，对某个样本点 Xi，我们都要找到一组 Wij，其中 j 属于Xi的邻近点的指标集合；而 Wij 要满足下面这个优化目标：

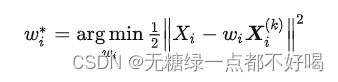
这里的含义是，我们要将这组 Wij 合并成一个向量 Wi，所希望的是 K 个邻近点经过这个系数向量线性组合后能够与 Xi 足够接近。

对于向量 Wi 来说，无论在高维空间还是低维空间都应该是同一个。那现在我们在低维空间的任务是通过高维空间寻找到的 Wi*，重构出一批低维数据 Y，使得这批低维数据之间的关系能用这个 Wi* 来刻画。

因此，低维空间要满足的优化目标是：

形象展示：

5.寻找一个最优解

通过前面的讲解，LLE 算法可以分为两步：

第一步，找到一个Wi*。其实，它是一个寻找优化问题的最优解：

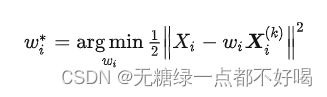
其中：我们假定样本以行向量形式出现，即Xi 是一个1行D列的向量，D是Xi 的维数；Xi,k 是其 k 个邻近点组合而成的矩阵，共有 k 行 D 列；wi 是一个行向量，列数为 k 列。

为了保证解的唯一性，对 wi 添加一个正则化约束：

其中：约束的含义是各分量之和为1，这里可以用全1矢量I（k行列向量，元素全为1）进行等价表示。

处理优化目标的项，通过拉格朗日函数求得最优解：

6.重构低维数据

第二步，通过找到的Wi*，重构出一批低维数据，使得这批低维数据之间的关系也能用这个 Wi* 来表示。其实，它是一个寻找优化问题的最优解：

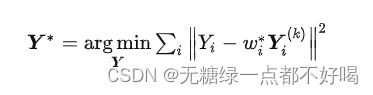
其中：低维中邻近点的编号应与高维一致，也就是说，高维空间中 X1 的邻近点是 X2，X3，则低维空间中Y1 的邻近点是 Y2，Y3；Y是一个 N 行 d 列的矩阵，N为样本数，d为它的维数；如果找到了Y，这代表完成了 D 维到 d 维的降维任务。

施加一个约束（令每列的 N 个数均值为 0，方差为 1）：

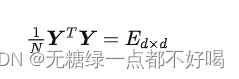
将 Wi* 进行扩展，改写目标函数，通过拉格朗日函数求得最优解：

通过以下微分形式的结论对带迹（trace）进行求导：

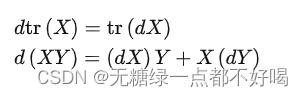
求偏导过程：

因此，只需让 Y 由矩阵(EN - W )(EN - W)T的d个特征向量组成即可；把求偏导的式子代入拉格朗日函数中，结果是λ ，也就是对应的特征值；而要使目标最小化，所以我们希望特征值尽可能小，因此最后取该矩阵的 d 个最小的特征值对应的特征向量组成Y。

7.总结

优点：
1）可以学习任意维的局部线性的低维流形；
2）算法归结为稀疏矩阵特征分解，计算复杂度相对较小，实现容易。

缺点：
1）算法所学习的流形只能是不闭合的，且样本集是稠密均匀的；
2）算法对最近邻样本数的选择敏感，不同的最近邻数对最后的降维结果有很大影响。

存在的问题：
当邻近点数k大于输入数据的维度D时，权重系数矩阵W不是满秩的。

Navier-Stokes方程

NS方程可以分为两个部分，连续性方程（continuity）和动量方程（momentum equation）。

---

总结

本周学习了 LLE 算法和 Navier-Stokes 方程，LLE是广泛使用的降维方法，它实现简单，但是对数据的流形分布特征有严格的要求。比如不能是闭合流形，不能是稀疏的数据集，不能是分布不均匀的数据集等，这限制了它的应用；对于Navier-Stokes 方程的学习，由于本周没有对NS方程的推导过程理解清楚，所以这次只介绍了NS的连续性方程和动量方程；下周我将继续学习降维方法和机器学习相关内容，会补充上python实现LLE算法，以及尝试理解并推导NS方程。