数据结构 —七大排序算法(图文详细版)
文章目录
- ⭐前言⭐
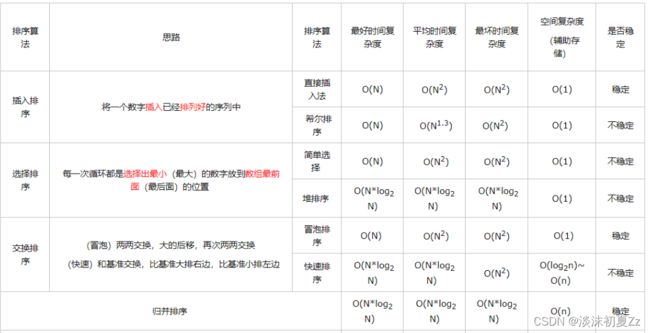
- 一,插入排序
-
- 1,直接插入排序
-
- (1)原理
- (2)实现`
- (3)稳定性-时间复杂度
- 2,希尔排序
-
- (1)原理
- (2)具体实现
- (3)稳定性-时间复杂度
- 二,选择排序
-
- 1,直接选择排序
-
- (1)原理
- (2)具体实现
- (3)稳定性-时间复杂度
- (4)优化-双向选择排序
- 2,堆排序
-
- (1)原理
- (2)实现-时间复杂度
- 三,交换排序
-
- 1,冒泡排序
-
- (1)原理
- (2)具体实现
- 2,快速排序
-
- (1)原理思路
- (2)具体分析
- (3)稳定性-时间复杂度
- 四,归并排序
-
- (1)原理
- (2)具体实现
- (3)稳定性-时间复杂度
⭐前言⭐
定义: 排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。平时的上下文中,如果提到排序,通常指的是排升序(非降序)。通常意义上的排序,都是指的原地排序
稳定性: 两个相等的数据,如果经过排序后,排序算法能保证其相对位置不发生变化,则我们称该算法是具备稳定性的排序算法
一,插入排序
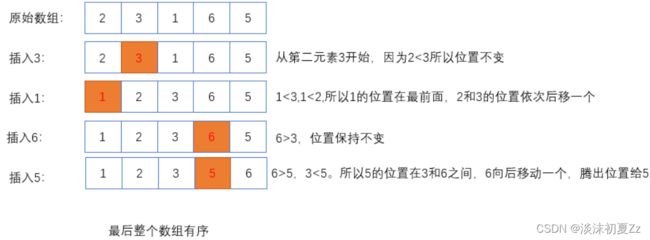
1,直接插入排序
(1)原理
首先分为有序区间(0,i),即(0,1),无序区间(i,n),默认第一个元素是有序的,每次选择无序区间的第一个元素,插入在有序区间的合适位置
(2)实现`
/**
* 直接插入排序
* 每次选择无序区间的第一个元素,插入到有序区间的合适位置
* @param arr
*/
public static void insertionSortBase(int[] arr) {
for (int i = 0; i < arr.length; i++) {
for (int j = i; j > 0 && arr[j-1]>arr[j]; j--) {
swap(arr,j,j-1);
// arr[j] > arr[j - 1]此时,循环直接终止
// j - 1已经是有序区间元素,大于前面的所有值
}
}
}
private static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
(3)稳定性-时间复杂度
⭐稳定性
根据查入的位置,插入排序在排序的过程中,始终保持元素的在整体元素中的相对位置不变,所以是稳定的排序算法。
⭐时间复杂度
通过分析可以知道,在最好的情况下,即是数组本身有序的情况下,只需要遍历一遍即可,这时候的时间复杂度取决于元素个数,为:O(n)。
在最坏的情况下,内外都要循环一次,所以这时候时间复杂度为O(n²)。
平均时间复杂度为:O(n²)
2,希尔排序
(1)原理
不断地进行gap分组,组内排序,直到gap=1时,整个数组插入排序。其中插入排序最外层是从gap走到数组的末尾,最内层是从gap索引向前看,看距离gap长度的元素,j为当前元素,j-gap是距离gap长的元素,两者进行比,当j-gap>=0,说明还有元素,交换元素的位置
(2)具体实现
/**
*希尔排序
* 不断地进行gap分组,组内排序,直到gap=1时,整个数组插入排序
*/
public static void shellSort(int[] arr) {
int gap = arr.length/2;
while(gap > 1){
//进行分组,组内插入排序
insertionSortGap(arr,gap);
gap/=2;
}
//整个数组的插入排序
insertionSortGap(arr,1);
}
/**
*根据gap分组,进行排序
* @param gap 传入的步长
*/
private static void insertionSortGap(int[] arr, int gap) {
//最外层是从gap走到数组的末尾
for (int i = gap; i < arr.length; i++) {
//最内层是从gap索引向前看
for (int j = i; j-gap>=0 && arr[j]<arr[j-gap]; j=j-gap) {
swap(arr,j,j-gap);
}
}
}
private static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
(3)稳定性-时间复杂度
稳定性
在排序完成后,两个相同的元素位置(上面图示的7*和7)位置发生了改变,所以是不稳定的
时间复杂度
介于O( n ^2)和O(nlogn)之间,视它的最好最坏以及平均复杂度具体分析
稳定性:
二,选择排序
1,直接选择排序
(1)原理
每次将无序区间最小值放在有序区间的第一个,开始默认第一个元素最小,有序区间[0,i),无序区间[i+1,n), 类似于冒泡,循环到最后一次有序
(2)具体实现
/**
* 直接选择排序
*/
public static void selectionSort(int[] arr) {
for (int i = 0; i < arr.length-1; i++) {
//min记录最小值
int min = i;
for (int j = i+1; j <arr.length ; j++) {
if(arr[j] < arr[min]){
min = j;
}
}
//此时min已经保存最小值下标,将min换到最前面
swap(arr,i,min);
}
}
private static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
(3)稳定性-时间复杂度
稳定性
假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。
时间复杂度
第一次内循环比较N - 1次,然后是N-2次,N-3次,……,最后一次内循环比较1次。
共比较的次数是 (N - 1) + (N - 2) + … + 1,求等差数列和,得 (N - 1 + 1)* N / 2 = N^2 / 2。
舍去最高项系数,其时间复杂度为 O(N^2)。
虽然选择排序和冒泡排序的时间复杂度一样,但实际上,选择排序进行的交换操作很少,最多会发生 N - 1次交换。
而冒泡排序最坏的情况下要发生N^2 /2交换操作。从这个意义上讲,交换排序的性能略优于冒泡排序。
(4)优化-双向选择排序
每一次从无序区间选出最小 + 最大的元素,存放在无序区间的最前和最后,直到全部待排序的数据元素排完 。
/**
* 双向选择排序
* @param array
*/
public static void selectSortOP(int[] array) {
int low = 0;
int high = array.length - 1;
// [low, high] 表示整个无序区间
// 无序区间内只有一个数也可以停止排序了
while (low <= high) {
int min = low;
int max = low;
for (int i = low + 1; i <= max; i++) {
if (array[i] < array[min]) {
min = i;
}
if (array[i] > array[max]) {
max = i;
}
}
swap(array, min, low);
if (max == low) {
max = min;
}
swap(array, max, high);
}
}
array = { 9, 5, 2, 7, 3, 6, 8 }; // 交换之前
// low = 0; high = 6
// max = 0; min = 2
array = { 2, 5, 9, 7, 3, 6, 8 }; // 将最小的交换到无序区间的最开始后
// max = 0,但实际上最大的数已经不在 0 位置,而是被交换到 min 即 2 位置了
// 所以需要让 max = min 即 max = 2
array = { 2, 5, 8, 7, 3, 6, 9 }; // 将最大的交换到无序区间的最结尾后
2,堆排序
(1)原理
(1)将无需序列构建成一个堆,根据升序降序需求选择大顶堆或小顶堆
(2)将堆顶元素与末尾元素交换,将最大元素"沉"到数组末端
(3)重新调整结构,使其满足堆定义,然后继续交换堆顶元素与当前末尾元素,反复执行调整+交换步骤,直到整个序列有序
(2)实现-时间复杂度
⭐ 博客链接:⭐
https://blog.csdn.net/qq_55660421/article/details/122380669
文章目录
一,堆排序
1,什么是堆排序
2,堆排序思想
3,代码实现
二,时间复杂度分析
1,初始化建堆
2,排序重建堆
3,总结
三,交换排序
1,冒泡排序
(1)原理
每次冒泡排序操作都会将相邻的两个元素进行比较,看是否满足大小关系要求,如果不满足,就交换这两个相邻元素的次序,一次冒泡至少让一个元素移动到它应该排列的位置,重复N次,就完成了冒泡排序。
(2)具体实现
/**
*冒泡排序法
*/
public void bubbleSort(int[] arr, int n){
if(n<=1){
return;
}
for(int i=0;i < n;i++){
boolean flag = false;
for (int j = 0; j < n-i-1; j++) {
if (arr[i - 1] > arr[i]) {
swap(arr, i - 1, i);
flag = true;
}
}
if(!flag) break;//没有数据交换,数组已经有序,退出排序
}
}
private static void swap(int[] arr, int i, int j) {
int temp = arr[i];
arr[i] = arr[j];
arr[j] = temp;
}
时间复杂度:
原操作(基本操作)为交换操作,当数组按从小到大有序排列时,基本操作执行次数为0,当自大到小有序排列时,基本操作次数为n(n-1)/2,一般情况下讨论算法在最坏的情况下时间复杂度(个别取平均),所以时间复杂度为O(n^2).
2,快速排序
(1)原理思路
快速排序主要采用分治的基本思想,每次将一个位置上的数据归位,此时该数左边的所有数据都比该数小,右边所有的数据都比该数大,然后递归将已归位的数据左右两边再次进行快排,从而实现所有数据的归位。
(2)具体分析
/**
* 在l..r上进行快速排序
* @param arr
* @param l
* @param r
*/
private static void quickSortInternal(int[] arr, int l, int r) {
// 递归终止时,小数组使用插入排序
if (r - l <= 15) {
insertBase(arr,l,r);
return;
}
//选择基准值,找到该值对应的下标
int p = partition(arr,l,r);
quickSortInternal(arr,l,p-1);
quickSortInternal(arr,p+1,r);
}
/**
* 在arr[l..r]上选择基准值,将数组划分为 < v 和 >= v两部分,返回基准值对应的元素下标
*/
private static int partition(int[] arr, int l, int r) {
//随机选择基准值
int randomIndex = random.nextInt(l,r);
swap(arr,l,randomIndex);
int v = arr[l];
// arr[l + 1...j] < v
int j = l;
// i是当前处理的元素下标
for (int i = l+1; i <= r; i++) {
if(arr[i] < v){
swap(arr,j+1,i);
// 小于v的元素值新增一个
j++;
}
}
// 此时j下标对应的就是最后一个 < v的元素,交换j和l的值,选取的基准值交换j位置
swap(arr,l,j);
return j;
}
(3)稳定性-时间复杂度
稳定性
快速排序有两个方向,左边的i下标一直往右走(当条件a[i] <= a[center_index]时),其中center_index是中枢元素的数组下标,一般取为数组第0个元素。
在中枢元素和a[j]交换的时候,很有可能把前面的元素的稳定性打乱,比如序列为 5 3 3 4 3 8 9 10 11
现在中枢元素5和3(第5个元素,下标从1开始计)交换就会把元素3的稳定性打乱。
所以快速排序是一个不稳定的排序算法,不稳定发生在中枢元素和a[j]交换的时刻。
时间复杂度
最坏情况,
需要进行n‐1递归调用,其空间复杂度为O(n),
平均情况为O(logn)。
四,归并排序
(1)原理
归并排序是一种概念上最简单的排序算法,与快速排序一样,归并排序也是基于分治法的。归并排序将待排序的元素序列分成两个长度相等的子序列,为每一个子序列排序,然后再将他们合并成一个子序列。合并两个子序列的过程也就是两路归并。
(2)具体实现
/**
* 在arr[l...r]上进行归并排序
* @param arr
* @param l
* @param r
*/
private static void mergeSortInternal(int[] arr, int l, int r) {
if (r - l<= 15) {
// 拆分后的小区间直接使用插入排序,不再递归
insertBase(arr,l,r);
return;
}
int mid = l + ((r - l) >> 1);
// 先排序左半区间
mergeSortInternal(arr,l,mid);
// 再排序右半区间
mergeSortInternal(arr,mid + 1,r);
// 不是上来就合并,当两个小区间之前存在乱序时才合并
if (arr[mid] > arr[mid + 1]) {
merge(arr,l,mid,r);
}
}
/**
* 将已经有序的arr[l..mid] 和[mid + 1..r]合并为一个大的有序数组arr[l...r]
* @param arr
* @param l
* @param mid
* @param r
*/
private static void merge(int[] arr, int l, int mid, int r) {
int[] temp = new int[r - l + 1];
// 将原数组内容拷贝到新数组中
for (int i = l; i <= r; i++) {
temp[i - l] = arr[i];
}
int i = l;
int j = mid + 1;
// k表示当前处理到原数组的哪个位置
for (int k = l; k <= r; k++) {
if (i > mid) {
arr[k] = temp[j - l];
j ++;
}else if (j > r) {
arr[k] = temp[i - l];
i ++;
}else if (temp[i - l] <= temp[j - l]) {
arr[k] = temp[i - l];
i ++;
}else {
arr[k] = temp[j - l];
j ++;
}
}
}
(3)稳定性-时间复杂度
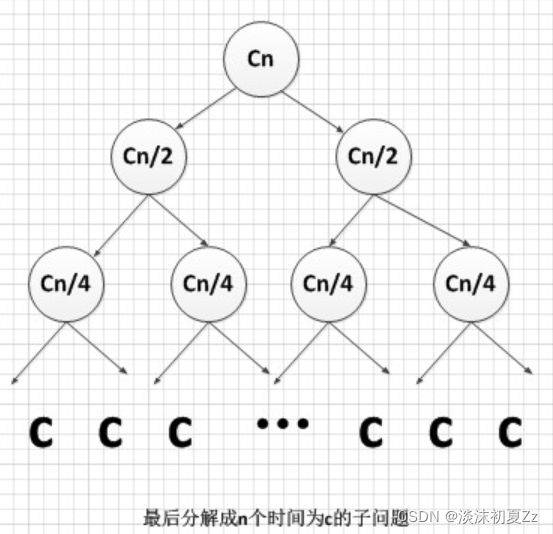
(1)可以说合并排序是比较复杂的排序,特别是对于不了解分治法基本思想的同学来说可能难以理解。总时间=分解时间+解决问题时间+合并时间。分解时间就是把一个待排序序列分解成两序列,时间为一常数,时间复杂度o(1).解决问题时间是两个递归式,把一个规模为n的问题分成两个规模分别为n/2的子问题,时间为2T(n/2).合并时间复杂度为o(n)。总时间T(n)=2T(n/2)+o(n).这个递归式可以用递归树来解,其解是o(nlogn).此外在最坏、最佳、平均情况下归并排序时间复杂度均为o(nlogn).从合并过程中可以看出合并排序稳定。
(2)从这个递归树可以看出,第一层时间代价为cn,第二层时间代价为cn/2+cn/2=cn…每一层代价都是cn,总共有logn+1层。所以总的时间代价为cn*(logn+1).时间复杂度是o(nlogn).