Python 之 平滑与过滤

平滑/过滤操作

我们对数据应用一些运算符，改变源点，以消除高频波动。

操作符的例子：scipy.signal.convolve、scipy.signal.medfilt、scipy.signal.savgol_filter等。

平滑算子是分布理论中具有特殊性质的平稳函数，用来建立一个平稳函数序列，用卷积来逼近一个平稳（广义）函数。直观地讲，拥有一个具有特殊特征的函数，并将其与一个平稳函数进行卷积，我们就会得到一个 "平稳函数"，在这个函数中，初始函数的特征被平滑化了，但函数仍然接近初始函数。

为了理解对数据的进一步操作，我们需要记住卷积这样一个操作。

卷积
卷积是函数分析中的一种操作，当应用于两个函数和时，返回第三个函数，对应于相互相关的函数()和(-)。

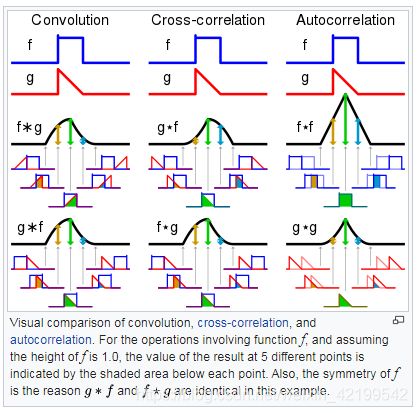
下图形象地解释了卷积、相互校正函数（MCC）和自相关的区别。

卷积运算可以解释为一个函数与另一个函数的反射和移位副本的 "相似性"。

卷积的概念被泛化为定义在任意可测量空间上的函数，并可被视为一种特殊类型的积分变换。

在离散的情况下，卷积对应的是的值与对应偏移值的系数之和，即(∗)()=(1)(−1)+(2)(−2)+(3)(−3)+…
一般来说，卷积是同时模拟一些过程的必要条件，它是基于一些现象的两个或多个模型的相互作用。

输入

import numpy as np

import matplotlib.pyplot as plt
%matplotlib inline

卷积的使用实例

生成复合数据

x = np.linspace(0, 2*np.pi, 100)
y = np.sin(x) + np.random.random(100) * 0.2

让我们定义平滑函数，用卷积来平滑源数据。

def smooth(y, box_pts):
    box = np.ones(box_pts) / box_pts
    y_smooth = np.convolve(y, box, mode='same')
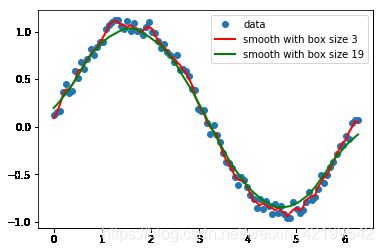
    return y_smooth

让我们来看看源数据平滑化的结果吧

plt.plot(x, y,'o', label='data')
plt.plot(x, smooth(y, 3), 'r-', lw=2, label='smooth with box size 3')
plt.plot(x, smooth(y, 19), 'g-', lw=2, label='smooth with box size 19')
plt.legend(bbox_to_anchor=(1, 1))
plt.show();

从图中可以看出，使用较大的窗口尺寸进行平滑处理，可以得到视觉上更平滑的曲线。

核密度估计

核平滑（KDE或核密度估计）是估计分布密度的非参数方法之一。与直方图法不同的是，估计分布的区块（窗口）不是固定的，而是以代表点为中心。

核密度估计是根据最终的数据样本对一个总体做出结论时的数据平滑任务。在一些领域，如信号处理和数理经济学，该方法也被称为Parzen-Rosenblatt窗口法。

该方法的两个重要参数是内核和窗口的宽度。核的选择主要影响最终分布的平稳性，但近似的精度受第二个参数的影响更大，所以窗口宽度的选择是一项重要的且不总是琐碎的工作（求助于交叉验证、不同的启发式方法或动态选择窗口宽度：见下文），但基本规则大致如下：样本分布越密集，窗口应该越窄。

Astropy是一个Python库，用于天文天体计算。

from astropy.modeling.models import Lorentz1D
from astropy.convolution import convolve, Gaussian1DKernel, Box1DKernel

1D Kernels

我们通过叠加使用均匀分布建模的噪声来创建合成数据。

lorentz = Lorentz1D(1, 0, 1)
x = np.linspace(-5, 5, 100)
data_1D = lorentz(x) + 0.1 * (np.random.rand(100) - 0.5)

我们将使用标准偏差为2像素的Gaussian1DKernel进行数据平滑。

gauss_kernel = Gaussian1DKernel(2)
smoothed_data_gauss = convolve(data_1D, gauss_kernel)

让我们使用5像素宽的Box1DKernel进行同样的数据平滑处理

box_kernel = Box1DKernel(5)
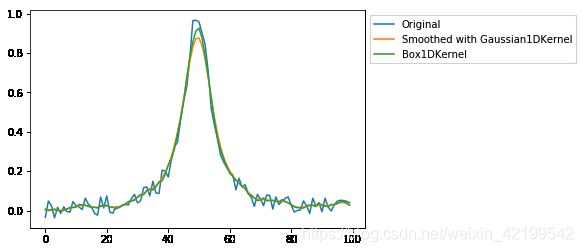
smoothed_data_box = convolve(data_1D, box_kernel)

查看结果

plt.plot(data_1D, label='Original')
plt.plot(smoothed_data_gauss, label='Smoothed with Gaussian1DKernel')
plt.plot(smoothed_data_box, label='Box1DKernel')
plt.legend(bbox_to_anchor=(1, 1))
plt.show();

当然，除了函数 astropy convolve 和 convolve_fft，你也可以通过传递属性数组来使用 numpy 或 scipy convolution 的内核。在大多数情况下，这将比天体卷积更快，但如果数据包含NaN值，将无法正常工作。

smoothed = np.convolve(data_1D, box_kernel.array)

plt.plot(data_1D, label='Original')
plt.plot(smoothed, label='Smoothed with numpy')
plt.legend(bbox_to_anchor=(1, 1))
plt.show();

2D Kernels

from astropy.convolution import convolve, Gaussian2DKernel, Tophat2DKernel
from astropy.modeling.models import Gaussian2D

创建合成数据

 

gauss = Gaussian2D(1, 0, 0, 3, 3)
# Fake image data including noise
x = np.arange(-100, 101)
y = np.arange(-100, 101)
x, y = np.meshgrid(x, y)
data_2D = gauss(x, y) + 0.1 * (np.random.rand(201, 201) - 0.5)

我们将使用标准偏差为2像素的Gaussian2DKernel进行数据平滑处理。

gauss_kernel = Gaussian2DKernel(2)
smoothed_data_gauss = convolve(data_2D, gauss_kernel)

让我们使用5像素宽的Tophat2DKernelel进行同样的数据平滑处理

tophat_kernel = Tophat2DKernel(5)
smoothed_data_tophat = convolve(data_2D, tophat_kernel)

展示结果

import seaborn as sns

pal = sns.light_palette("navy", as_cmap=True)

ax = plt.axes()
sns.heatmap(data_2D, ax=ax, cmap=pal)
ax.set_title('Data')
plt.show();

ax = plt.axes()
sns.heatmap(smoothed_data_gauss, ax=ax, cmap=pal)
ax.set_title('Smoothed with Gaussian1DKernel')
plt.show();

ax = plt.axes()
sns.heatmap(smoothed_data_tophat, ax=ax, cmap=pal)
ax.set_title('Smoothed with Tophat2DKernel')
plt.show();

高斯核的平滑性比Top Hat更好。

过滤器

和其他源信号处理

滤波器Savitsky-Goley
Savitsky-Goley滤波器是一种数字滤波器，它可以应用于数据集以使其平滑，即在不失真原始信号的情况下提高数据的准确性。这是在一个称为卷积的过程中实现的，通过对线性最小二乘法拟合具有低多项式的相邻数据点的连续子集。当数据点分布均匀时，可以找到最小二乘方程的解析解，作为一组 "光系数"。这些系数可以应用于所有数据的子集，以获得每个子集中心点的平滑信号（或衍生的平滑信号）的估计。

即使是来自非周期性和非线性源的噪声样本，该方法也能很好地工作。

from scipy.signal import savgol_filter

yhat = savgol_filter(y, 51, 3) # window size 51, polynomial order 3

plt.plot(x,y)
plt.plot(x,yhat, color='red')
plt.show();