一文彻底搞懂逻辑回归模型

1.逻辑回归

  逻辑回归(Logistic regression，简称LR)虽然其中带有"回归"两个字，但逻辑回归其实是一个分类模型，并且广泛应用于各个领域之中。 将线性回归模型得到的结果通过一个非线性的$sigmoid$函数,得到$[0,1]$之间取值范围的值，同时设置阈值为$0.5$，通过与阈值的比较达到二分类的效果,即为逻辑回归模型。

  关于逻辑回归，可以用一句话总结：假设数据服从伯努利分布(0-1分布)，通过极大似然函数的方法，运用梯度下降法求解参数，来达到将数据二分类的目的。

2.sigmoid函数

2.1 sigmoid函数公式

逻辑回归就是基于sigmoid函数构建模型，该函数公式如下
$$g(z)=\frac{1}{1+e^{(-z)}}$$
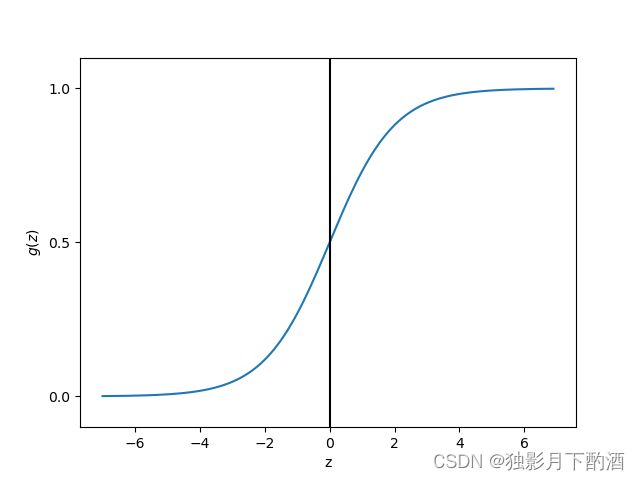
使用Python的numpy，matplotlib对该函数进行可视化，如下：

# 绘制[-7,7]的sigmod函数图像
import matplotlib.pyplot as plt
import numpy as np


def sigmod(z):
    return 1.0 / (1.0 + np.exp(-z))


z = np.arange(-7, 7, 0.1)
phi_z = sigmod(z)
plt.plot(z, phi_z)
plt.axvline(0.0, color='k')
plt.axhspan(0.0, 1.0, facecolor='1.0', alpha=1.0, ls="dotted")
plt.yticks([0.0, 0.5, 1.0])
plt.ylim(-0.1, 1.1)
plt.xlabel('z')
plt.ylabel('$g(z)$')
plt.show()

逻辑回归模型直观上看：
$$y_{\_pred}=\frac{1}{1+e^{-(w_0+w_1\ast x_1+w_2\ast x_2+...+w_n\ast x_n)}}$$
线性回归模型套上了$sigmoid$函数就输出值压缩到了$(0,1)$之间，设置阈值$0.5$即可分类。

2.2 sigmoid函数的性质

• 将任意的输入压缩到$(0,1)$之间
• 函数在$z=0$处的导数最大
• 设$f(x)=sigmoid(x)$,$f(x)$的导函数为:$\frac{\partial f(x)}{\partial x}=f(x)(1-f(x))$
• 函数两边梯度趋于饱和(容易导致梯度消失)
• 函数不以原点为中心

2.3 逻辑回归使用sigmoid函数的原因

  对于一般的线性回归模型，我们知道:自变量$X$和因变量$Y$都是连续的数值,通过$X$的输入就可以很好的预测$Y$值。在实际生活中，离散的数据类型也是比较常见的，比如好和坏,男和女等等。那么问题来了：在线性回归模型的基础上，是否可以实现预测一个因变量为离散数据类型的模型呢？

答案当然是可以的。我们可能会想想到阶跃函数：
$$f(n)=\{\begin{array}{ll}0,& ifz<0\\ 0.5,& ifz=0\\ 1,& ifz>0\end{array}$$
但是用在这里是不合适的，正如我们神经网络激活函数不选择阶跃函数的原因一样，因为它不连续不可微。 而能满足分类效果，且是连续的函数，sigmoid函数是再好不过的选择了。因此逻辑回归模型是在线性回归模型的基础上，套一个sigmoid函数，得到一个处于[0,1]之间的数值，同时设置一个阈值，通过与阈值的比较来实现分类的效果。

3.逻辑回归的假设

逻辑回归的假设条件主要是两个：

（1）假设数据服从伯努利分布

（2）假设模型的输出值是样本为正例的概率

基于这两个假设，我们可以分别得出类别为$1$和$0$的后验概率估计：
$$\begin{gathered} P(y=1|x,\theta )=h_{\theta }(x)=\frac{1}{1+e^{-x\theta }} \\ P(y=0|x,\theta )=h_{\theta }(x)=\frac{e^{-x\theta }}{1+e^{-x\theta }} \end{gathered}$$

4.逻辑回归的损失函数

  有了模型，我们自然会想到要求策略，也就是损失函数。对于逻辑回归，很自然想到：用线性回归的损失函数"离差平方和"的形式是否可以？

  但事实上，这种形式并不适合，因为所得函数并非凸函数，而是有很多局部的最小值，这样不利于求解。

  前面说到逻辑回归其实是概率类模型，因此，我们通过极大似然估计(MLE)推导逻辑回归损失函数(交叉熵损失函数)。 下面是具体推导过程。

① 通过基本假设得到了$1$和$0$两类的后验概率，现在将两个概率合并可得：
$$P(y=1|x,\theta )=h_{\theta }(x{)}^y(1-h_{\theta }(x){)}^{1-y}y\in \{0,1\}$$
② 使用极大似然估计来根据给定的训练数据集估计出参数，将n个训练样本的概率相乘得到：
$$L(\theta )=\prod _{i=1}^{n}P(y^{(i)}|x^{(i)},\theta )=\prod _{i=1}^n{h}_{\theta }(x^{(i)},\theta {)}^{y^{(i)}}[1-h_{\theta }(x^{(i)},\theta ){]}^{1-y^{(i)}}$$
③ 似然函数是相乘的模型，可以通过取对数将等式右侧变为相加模型，然后将指数提前，以便于求解。变换后如下：
$$l(\theta )=ln(L(\theta ))=\sum _{i=1}^n{y}^{(i)}ln[h_{\theta }(x^{(i)},\theta )]+(1-y^{(i)})ln[1-h_{\theta }(x^{(i)},\theta )]$$
④ 如此就推导出了参数的最大似然估计。我们的目的是将所得似然函数极大化，而损失函数是最小化，因此，我们需要在上式前加一个负号便可得到最终的损失函数。
$$J(\theta )=-l(\theta )=-\left(\sum _{i=1}^n{y}^{(i)}ln[h_{\theta }(x^{(i)},\theta )]+(1-y^{(i)})ln[1-h_{\theta }(x^{(i)},\theta )]\right)$$

$$J(h_{\theta }(x^{(i)};\theta ),y;\theta )=-yln(h_{\theta }(x;\theta ))-(1-y)ln(1-h_{\theta }(x;\theta ))$$

其等价于：
$$J(h_{\theta }(x^{(i)};\theta ),y;\theta )=\{\begin{array}{ll}-ln(h_{\theta }(x;\theta )),& ify=1\\ -ln(1-h_{\theta }(x;\theta )),& ify=0\end{array}$$

5.逻辑回归损失函数的求解

  现在我们推导出了逻辑回归的损失函数，而需要求解是模型的参数$\theta$，即线性模型自变量的权重系数。 对于线性回归模型而言，可以使用最小二乘法，但对于逻辑回归而言使用传统最小二乘法求解是不合适的。
$$J(\theta )=\sum _{i=1}^n{\left(y^{(i)}-\frac{1}{1+e^{-{\theta }^T{x}^{(i)}}}\right)}^2$$
  对于不适合的解释原因有很多，但本质上不能使用经典最小二乘法的原因在于：$logistic$回归模型的参数估计问题不能“方便地”定义“误差”或者“残差”。 因此，考虑使用迭代类算法优化，常见的就是梯度下降法。当然，还有其它方法比如，坐标轴下降法，牛顿法等。我们本篇介绍使用”梯度下降法“来对损失函数求解。

使用梯度下降法求解逻辑回归损失函数 梯度下降的迭代公式如下：
$$\begin{array}{rl}{\theta }_j& ={\theta }_j+{\Delta }_j\\ & ={\theta }_j-\eta \frac{\partial J(\theta )}{\partial {\theta }_j}\end{array}$$
问题变为如何求损失函数对参数$\theta$的梯度。下面进行详细推导过程：
$$\begin{array}{rl}\frac{\partial J(\theta )}{\partial \theta }& =-\sum _{i=1}^n\left(y^{(i)}\frac{1}{h_{\theta }(x^{(i)};\theta )}\frac{\partial h_{\theta }(x^{(i)};\theta )}{\partial \theta }+(1-y^{(i)})\frac{1}{1-h_{\theta }(x^{(i)};\theta )}\frac{\partial (1-h_{\theta }(x^{(i)};\theta ))}{\partial \theta }\right)\\ & =-\sum _{i=1}^n\left(y^{(i)}\frac{1}{h_{\theta }(x^{(i)};\theta )}{h}_{\theta }(x^{(i)};\theta )[1-h_{\theta }(x^{(i)};\theta )]x^{(i)}+(1-y^{(i)})\frac{1}{1-h_{\theta }(x^{(i)};\theta )}-[1-h_{\theta }(x^{(i)};\theta )]h_{\theta }(x^{(i)};\theta )x^{(i)}\right)\\ & =-\sum _{i=1}^n\left(y^{(i)}[1-h_{\theta }(x^{(i)};\theta )]-(1-y^{(i)})h_{\theta }(x^{(i)};\theta )\right)x^{(i)}\\ & =\sum _{i=1}^n\left(h_{\theta }(x^{(i)};\theta )-y^{(i)}\right)x^{(i)}\end{array}$$
最后将求得的梯度带入迭代公式中，即为:
$$\begin{array}{rl}{\theta }_j& ={\theta }_j+{\Delta }_j\\ & ={\theta }_j-\eta \frac{\partial J(\theta )}{\partial {\theta }_j}\\ & ={\theta }_j-\eta \sum _{i=1}^n\left(h_{\theta }(x^{(i)};\theta )-y^{(i)}\right)x^{(i)}\end{array}$$

注意：公式中，$i$ 代表样本数，$j$ 代表特征数。

6.逻辑回归的优缺点

6.1 优点

1）LR能以概率的形式输出结果，而非只是0,1判定。

2）LR的可解释性强，可控度高

3）训练快，feature engineering之后效果赞。

4）因为结果是概率，可以做ranking model。

6.2 缺点

1）容易欠拟合，一般准确度不太高

2）分类精度可能不高， 因为形式非常的简单，很难去拟合数据的真实分布。

7.逻辑回归的特征离散化

Q：LR模型为什么对特征进行离散化？

• 非线性！非线性！非线性！逻辑回归属于广义线性模型，表达能力受限；单变量离散化为N个后，每个变量有单独的权重，相当于为模型引入了非线性，能够提升模型表达能力，加大拟合； 离散特征的增加和减少都很容易，易于模型的快速迭代；
• 速度快！速度快！速度快！稀疏向量内积乘法运算速度快，计算结果方便存储，容易扩展；
• 鲁棒性！鲁棒性！鲁棒性！离散化后的特征对异常数据有很强的鲁棒性：比如一个特征是年龄>30是1，否则0。如果特征没有离散化，一个异常数据“年龄300岁”会给模型造成很大的干扰；
• 方便交叉与特征组合：离散化后可以进行特征交叉，由$M+N$个变量变为$M\ast N$个变量，进一步引入非线性，提升表达能力；
• 稳定性：特征离散化后，模型会更稳定，比如如果对用户年龄离散化，$20-30$作为一个区间，不会因为一个用户年龄长了一岁就变成一个完全不同的人。当然处于区间相邻处的样本会刚好相反，所以怎么划分区间是门学问；
• 简化模型：特征离散化以后，起到了简化了逻辑回归模型的作用，降低了模型过拟合的风险。

8.总结

1）逻辑回归即为数据服从伯努利分布,通过极大似然函数的方法，运用梯度下降法求解参数,来达到二分类的目的。

2）逻辑回归是一个分类模型，解决分类问题(类别+概率)，可以做ranking model。

本文仅作为个人学习记录使用, 不用于商业用途, 谢谢您的理解合作。