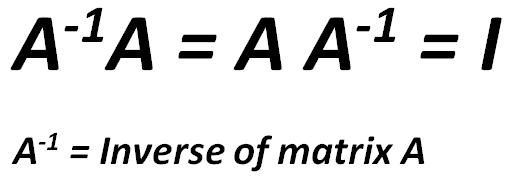numpy 矩阵与向量相乘_NumPy解释线性代数

机器学习和深度学习模型需要大量的数据。它们的性能在很大程度上取决于数据量。因此，我们倾向于收集尽可能多的数据，以建立一个稳健和准确的模型。数据以多种不同的格式收集，从数字到图像，从文本到声波。然而，我们需要将数据转换为数字以便对其进行分析和建模。

仅仅将数据转换为标量(单个数字)是不够的。随着数据量的增加，使用标量的操作开始变得低效。我们需要向量化或矩阵运算来有效地进行计算。这就是线性代数发挥作用的地方。

线性代数是数据科学领域的重要课题之一。在这篇文章中，我们将通过使用NumPy的例子来介绍线性代数的基本概念。

NumPy是Python的一个科学计算库，是许多库(比如Pandas)的基础。

---

线性代数中的对象类型

线性代数中的对象(或数据结构)类型：

• 标量：单个数字
• 向量：数字数组
• 矩阵：二维数字数组
• 张量：N>2的N维数列

标量就是一个数字。我们将在下面的示例中看到，它可以用于向量化操作。

向量是一组数字。例如，5个元素的向量：

我们可以在向量化运算中使用标量。对向量的每个元素执行指定的操作。例如

矩阵是二维向量

它看起来像是一个包含行和列的pandas数据框。实际上，pandas数据帧被转换成矩阵，然后输入到机器学习模型中。

张量是一个N维数数组，其中N大于2。张量主要用于输入数据为三维的深度学习模型。

很难用数字来表示，但是可以把T看成3个3x2形状的矩阵。

shape方法可用于检查numpy数组的形状。

数组的大小是通过乘以每个维度的大小来计算的。

---

常用矩阵术语

如果行数等于列数，矩阵称为方阵。因此，上面的矩阵A是一个方阵。

单位矩阵，表示为I，是一个方阵，对角线上有是，其他位置全是0。NumPy的identity函数可以用来创建任意大小的单位矩阵。

一个单位矩阵的特殊之处在于矩阵乘上它不会改变。从这个意义上讲，它与实数中的数字1相似。我们将在这篇文章的矩阵乘法部分用单位矩阵做例子。

矩阵的逆矩阵是与原始矩阵相乘得到单位矩阵的矩阵。

不是每个矩阵都有一个逆矩阵。如果矩阵A有一个逆矩阵，那么它被称为可逆或非奇异

---

点乘与矩阵乘法

点乘和矩阵乘法是复杂机器学习和深度学习模型的组成部分，因此对它们进行全面的了解是非常有价值的。

两个向量的点积是元素相对于其位置的乘积之和。第一个向量的第一个元素乘以第二个向量的第一个元素，依此类推。这些积的和就是点积。在NumPy中计算点积的函数是dot()。

让我们首先以numpy数组的形式创建两个简单的向量并计算点积。

点积计算为(1*2)+(2*4)+(3*6)，即28。

因为我们在相同的位置相乘，所以这两个向量的长度必须相同才能得到点积。

在数据科学领域，我们主要处理矩阵。矩阵是一组以结构化方式组合的行和列向量。因此，两个矩阵的相乘涉及向量的许多点积运算。我们再看一些例子就会更清楚了。我们先用NumPy创建两个2x2矩阵。

2x2矩阵有2行2列。行和列的索引以0开头。例如，A(索引为0的行)的第一行是[4,2]的数组。A的第一列是[4,0]的数组。第一行和第一列的元素是4。

我们可以访问单个行、列或元素，如下所示：

这些是理解矩阵乘法的重要概念。

两个矩阵的相乘涉及到第一个矩阵的行和第二个矩阵的列之间的点乘。第一步是A的第一行和B的第一列之间的点积。这个点积的结果是在位置[0,0](即第一行，第一列)处得到的矩阵的元素。

因此，得到的矩阵C在第一行和第一列将有一个 (4*0) + (2*4) 。C[0,0]=18。

下一步是A的第一行和B的第二列的点积。

C在第一行和第二列有一个(4*0)+(2*4)。C[0,1]=8。

第一行A已完成，因此我们从A的第二行开始，并遵循相同的步骤。

C在第二行和第一列有一个(0*4)+(3*1)。C[1,0]=3。

最后一步是A的第二行和B的第二列之间的点积。

C在第二行和第二列有一个(0*0)+(3*4)。C[1,1]=12。

我们已经看到它是如何一步一步完成的。所有这些操作都是用np.dot操作：

你可能还记得，我们已经提到过，单位矩阵乘以任何矩阵时不会改变矩阵。让我们举个例子。

我们还提到，当一个矩阵乘以它的逆矩阵时，结果就是单位矩阵。让我们先创建一个矩阵，然后求它的逆矩阵。我们可以利用NumPy函数linalg.inv()求矩阵的逆。

用B的逆矩阵C乘以B：

我们得到了单位矩阵。

---

正如我们在向量点积中回忆的那样，两个向量的长度必须相同才能有一个点积。矩阵乘法中的每个点积运算都必须遵循这个规则。点积是在第一个矩阵的行和第二个矩阵的列之间进行的。因此，第一个矩阵的行和第二个矩阵的列的长度必须相同。

矩阵乘法的要求是第一个矩阵的列数必须等于第二个矩阵的行数。

例如，我们可以用一个3x2矩阵乘以一个2x3矩阵。

结果矩阵的形状将是3x3，因为我们对A的每一行进行3点积运算，A有3行。确定结果矩阵形状的一种简单方法是从第一个矩阵中提取行数，从第二个矩阵中提取列数：

• 3x2和2x3相乘返回3x3
• 3x2和2x2相乘返回3x2
• 2x4和4x3相乘返回2x3

---