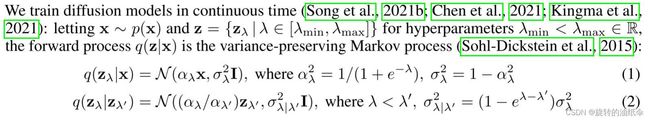Classifier-Free Diffusion Guidance【论文精读加代码实战】

0、前言

论文地址：Classifier-Free Diffusion Guidance
在这篇博文中将会详细介绍Classifier-Free Diffusion Guidance的原理，公式推导，应用场景和代码分析。
然后是分析classifier guided diffusion和Classifier-Free Diffusion Guidance的区别和联系，以及各自的优缺点。
其中代码来自：openai的GLIDE: a diffusion-based text-conditional image synthesis model其论文地址：GLIDE: Towards Photorealistic Image Generation and Editing with Text-Guided Diffusion Models代码地址：https://github.com/openai/glide-text2im

	Classifier-Free Diffusion Guidance	classifier guided diffusion
缺点	1、需要额外训练两个模型，成本较大，但可以实现比较精细的控制。 2、采样速度慢，分类器可以比生成模型更小且更快，因此分类器引导的采样可以比无分类器引导更快，因为后者需要运行扩散模型的两个前向通道，一个用于条件得分，另一个用于无条件得分。	1、需要训练额外的分类器,并且该分类器必须在有噪声的数据上训练，因此通常不可能插入预先训练的分类器。 2、因为分类器引导在采样期间将分数估计与分类器梯度混合，所以分类器引导的扩散采样可以被解释为试图将图像分类器与基于梯度的对抗性攻击混淆。（与GAN的训练有点类似）
优点	1、无需分类器，但能达到classifier guidance的效果 2、简单，其训练方式只需修改一行代码，即随机将c置为$\varnothing$(to randomly drop out the conditioning)，在采样过程中混合conditional模型和unconditional模型的分数估计。 3、其扩散模型是由无约束神经网络参数化的，因此它们的得分估计不一定形成保守的向量场，这与分类器梯度不同。	1、采样速度快 2、可以直接用训练好的一个SOTA级别的扩散模型，可以低成本实现简单的控制

1、Classifier-Free Diffusion Guidance介绍

1.1原理介绍

这里和DDPM的区别是，将之前离散的时间步time_steps变为了连续的时间continuous time。

其中x是给定的数据
z是x加噪的过程($z_{\lambda }$)
而$\lambda$是$z_{\lambda }$的对数信噪比，其中${\lambda }_{min}$可以看作是纯高斯噪声，${\lambda }_{max}$是原始数据x
前行过程显然是从数据到纯噪声，故是在减小$\lambda$的方向上进行。
这里的$\lambda$在Kingma et al.,2021介绍了，感兴趣的可以去看看。与之对应的方差和均值的表示都有一些不同，我们只需记住即可。

给定条件c来逐步预测数据$z_{\lambda }$，其中均值和方差是给定的形式，这里参考【2】IDDPM对方差进行了学习。

我们其实有三种预测方法：
一：预测上一步数据分布的均值
二：直接预测$x_0$
三：预测上一步数据分布的噪声$ϵ$（可以得到均值）。
在DDPM中作者发现预测上一步数据分布的均值的效果最好。从而得到最终的训练函数。

这里的训练函数其实是等同于score-based generative models的去噪分数匹配的denoising score matching。

类似于DDPM里面的$\beta$
这里的$p(\lambda )$可以是$[{\lambda }_{min},{\lambda }_{max}]$的均匀分布，或者余弦cosine分布，或者这里给出的双曲正割分布(具体细节看上面的公式)

1.2Classifier-Guidance

从方法上来看，条件控制生成的方式分两种：事后修改（Classifier-Guidance）和事前训练（Classifier-Free）。其中Classifier-Guidance这这篇文章有详细介绍：classifier guided diffusion

上图主要想表达的是随着分类器引导强度的不断增强，初始得分Inception score会提升但样本多样性会降低。
即从每个类的条件分布都是各向同性高斯分布isotropic Gaussian，到每个条件将概率质量放置在远离其他类别并且朝向由逻辑回归给出的高置信度的方向，并且大部分质量变得集中在较小的区域中。

一个有趣的结论是：将具有权重w + 1的分类器指导应用于无条件unconditional模型在理论上将导致与将具有权重w的分类器指导应用于有条件conditional模型相同的结果，

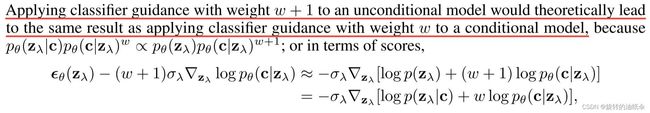
Classifier-Guidance主要困难就是分类器的训练，由于扩散模型逐渐对输入噪声去噪，因此任何用于引导的分类器也需要能够应对高水平噪声，以便它可以在整个采样过程中提供有用的信息。这通常需要训练定制的分类器，在这一点上，端到端地训练传统条件生成模型更容易。

此外，即使我们有一个噪声鲁棒的分类器，classifier guidance 的有效性在本质上也是有限的：输入$x_t$中的大多数信息与预测标签y无关，因此，采用分类器关于其输入的梯度可以在输入空间中产生任意（甚至是对抗）的方向。

1.3CLASSIFIER-FREE GUIDANCE（最重要）

算法1和2详细描述了无分类器指导的训练和采样。
需要训练两个模型(即${ϵ}_{\theta }(z_t,c)$和${ϵ}_{\theta }(z_t)$)，即无条件模型和有条件模型，可以单独训练也可以联合训练，作者这里是联合训练，因为它实现起来非常简单，不会使训练pipeline,复杂化，并且不会增加参数的总数。只是需要以$p_{uncond}$(超参数)的概率使c为$\varnothing$。
采样过程的$\omega$也是超参数。采样的步数SAMPLING STEPS也是。
可见新鲜的地方就是在conditional model${ϵ}_{\theta }(z_t,c)$和unconditional model${ϵ}_{\theta }(z_t)$，训练这两个模型，然后在采样的时候进行一个插值。

方程式(6)不存在分类器梯度，因此在${\widetilde{ϵ}}_{\theta }$方向上采取步骤不能被解释为对图像分类器的基于梯度的对抗性攻击。此外，由于使用无约束神经网络，从是非保守向量场的分数估计来构造，因此通常不存在标量势，例如分类器对数似然，其中${\widetilde{ϵ}}_{\theta }$是分类器引导的分数。

根据贝叶斯公式，提出了一种implicit classifier隐式分类方法。

CLASSIFIER-FREE GUIDANCE为什么比 classifier guidance 好得多？主要原因是我们从生成模型构造了“分类器”，而标准分类器可以走捷径：忽视输入x 依然可以获得有竞争力的分类结果，而生成模型不容易被糊弄，这使得得到的梯度更加稳健。

值得注意的是，classifier-free guidance的想法发布和 OpenAI 的 GLIDE 模型只间隔很短的时间，后者利用它产生了显著的效果 – 以至于这个想法有时归因于后者！

2、总结

对于大多数人来说，一个SOTA级别的扩散模型训练成本太大了，而分类器（Classifier）的训练还能接受，所以就想着直接复用别人训练好的无条件扩散模型，用一个分类器来调整生成过程以实现控制生成，这就是事后修改的Classifier-Guidance方案；而对于“财大气粗”的Google、OpenAI等公司来说，它们不缺数据和算力，所以更倾向于往扩散模型的训练过程中就加入条件信号，达到更好的生成效果，这就是事前训练的Classifier-Free方案。

Classifier-Free方案，最早出自《Classifier-Free Diffusion Guidance》，后来的DALL·E 2、Imagen等吸引人眼球的模型基本上都是以它为基础做的。

说白了，Classifier-Free方案就是训练成本大，本身“没什么技术含量”。

本文简单介绍了建立条件扩散模型的相关理论结果，主要包含事后修改（Classifier-Guidance）和事前训练（Classifier-Free）两种方案。其中，前者不需要重新训练扩散模型，可以低成本实现简单的控制；后者需要重新训练扩散模型，成本较大，但可以实现比较精细的控制。

3、代码分析

3.1模型

${ϵ}_{\theta }\left(\mathbf{x}\right)$使用 UNet 模型，改动之处是模型输入增加数据标签，即 tokens 和 mask，参见代码glide_text2im/text2im_model.py/Text2ImUNet【5】：

    def forward(self, x, timesteps, tokens=None, mask=None):
        hs = []
        emb = self.time_embed(timestep_embedding(timesteps, self.model_channels))
        if self.xf_width:
            text_outputs = self.get_text_emb(tokens, mask)
            xf_proj, xf_out = text_outputs["xf_proj"], text_outputs["xf_out"]
            emb = emb + xf_proj.to(emb)
        else:
            xf_out = None
        h = x.type(self.dtype)
        for module in self.input_blocks:
            h = module(h, emb, xf_out)
            hs.append(h)
        h = self.middle_block(h, emb, xf_out)
        for module in self.output_blocks:
            h = th.cat([h, hs.pop()], dim=1)
            h = module(h, emb, xf_out)
        h = h.type(x.dtype)
        h = self.out(h)
        return h

3.2数据加载

数据加载：希望得到模型可以无条件解噪和有条件解噪，实现这一点很简单，以一定的概率（通常为10-20%）将标签替换为”[$\varnothing$]”，详细代码参见glide_finetune/load.py/TextImageDataset【5】：

def get_uncond_tokens_mask(tokenizer: Encoder):
    uncond_tokens, uncond_mask = tokenizer.padded_tokens_and_mask([], 128)
    return th.tensor(uncond_tokens), th.tensor(uncond_mask, dtype=th.bool)

def __getitem__(self, ind):
    if self.text_files is None or random() < self.uncond_p:
        tokens, mask = get_uncond_tokens_mask(self.tokenizer)
    else:
        tokens, mask = self.get_caption(ind)

3.3生成图像

step1：生成 tokens 和 mask

如果要生成 1 张 64×64 的图像，输入prompt为 ”an oil painting of a garden“，即 batchsize 为 1，会随机初始化 2 张高斯图像，一个图像的标签为 tokens，另一个图像标签为 uncond_tokens，tokens 和 uncond_tokens 合并成一个张量， shape 为 (2batchsize, text_ctx)，其中 text_ctx 为设置的 tokens 长度，比如取128，即将所有的 prompt encode 成 128 维度， 因为给的 prompt 只有6个单词，剩余的122个 tokens 人为地赋予一个值，即做 padding，为了将单词与 padding 的值区分开来，需要用到mask，6个单词位置 mask 为 true，padding 位置设为 false，所以 mask 的 shape 也为 (2batchsize, text_ctx)，核心代码如下【4】：

tokens, mask = model.tokenizer.padded_tokens_and_mask(tokens, options['text_ctx'])
uncond_tokens, uncond_mask = model.tokenizer.padded_tokens_and_mask([], options['text_ctx'])

model_kwargs = dict(
    tokens=th.tensor(
        [tokens] * batch_size + [uncond_tokens] * batch_size, device=device
    ),
    mask=th.tensor(
        [mask] * batch_size + [uncond_mask] * batch_size,
        dtype=th.bool,
        device=device,
    ),
)

step2：模型运算

模型的输入为 x_t (torch.Size([2, 3, 64, 64]))，ts (torch.Size([2]))，**kwargs (tokens, mask)， 经过 UNet 后 输出 (2, 6, 64, 64)，其中维度1会拆分成2部分，分别为 eps 和 rest ，其中 eps 将用于计算 model_mean，rest 用于计算model_variance；eps 在维度0 继续拆分成2部分： cond_eps 和 uncond_eps，对 cond_eps 和 uncond_eps 使用上章节的方法进行处理，最后通过 diffusion 生成结果，最后的图像取 [:batch_size]，核心代码如下【5】：

def model_fn(x_t, ts, **kwargs):
    # torch.Size([2, 3, 64, 64]), torch.Size([2])
    half = x_t[: len(x_t) // 2]
    combined = th.cat([half, half], dim=0)
    # torch.Size([2, 3, 64, 64])
    model_out = model(combined, ts, **kwargs)
    # torch.Size([2, 6, 64, 64])
    eps, rest = model_out[:, :3], model_out[:, 3:]
    # torch.Size([2, 3, 64, 64]) torch.Size([2, 3, 64, 64])
    cond_eps, uncond_eps = th.split(eps, len(eps) // 2, dim=0)
    # torch.Size([1, 3, 64, 64]) torch.Size([1, 3, 64, 64])
    half_eps = uncond_eps + guidance_scale * (cond_eps - uncond_eps)
    eps = th.cat([half_eps, half_eps], dim=0)
     # torch.Size([2, 3, 64, 64])
    return th.cat([eps, rest], dim=1)  # torch.Size([2, 6, 64, 64])

model_output = model(x, t, **model_kwargs)
# model_output: torch.Size([2, 6, 64, 64])
model_output, model_var_values = th.split(model_output, C, dim=1)
# model_output: torch.Size([2, 3, 64, 64]); model_var_values: torch.Size([2, 3, 64, 64])
    
min_log = _extract_into_tensor(self.posterior_log_variance_clipped, t, x.shape)
max_log = _extract_into_tensor(np.log(self.betas), t, x.shape)
frac = (model_var_values + 1) / 2
model_log_variance = frac * max_log + (1 - frac) * min_log
model_variance = th.exp(model_log_variance)
# model_variance: torch.Size([2, 3, 64, 64])

pred_xstart = process_xstart(self._predict_xstart_from_eps(x_t=x, t=t, eps=model_output))
# pred_xstart: torch.Size([2, 3, 64, 64])
model_mean, _, _ = self.q_posterior_mean_variance(x_start=pred_xstart, x_t=x, t=t)
# model_mean: torch.Size([2, 3, 64, 64])

samples = diffusion.p_sample_loop(
    model_fn,
    (full_batch_size, 3, options["image_size"], options["image_size"]),
    device=device,
    clip_denoised=True,
    progress=True,
    model_kwargs=model_kwargs,
    cond_fn=None,
)[:batch_size]
# samples: torch.Size([1, 3, 64, 64])

注意：这里的采样公式略有不同，代码中用的是：

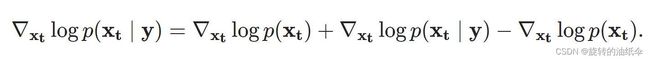
为了在 classifier-free guidance 中使用通用文本prompts，在训练中有时会将文本替换为空序列(表示为∅)，随后使用更新的${ϵ}_{\theta }(z_t|y)$指导生成标签为y的图像：

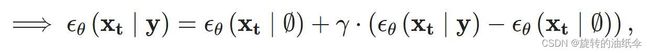
当 $\gamma =0$为无条件模型；当 $\gamma =1$为标准的条件概率模型。当 $\gamma >1$时，神奇的事情就发生了，以下是 OpenAI 的使用classifier-free guidance的 GLIDE model【5】例子：

来自 OpenAI 的 GLIDE 模型的两组样本，提示为“熊猫吃竹子的彩色玻璃窗。”，取自他们的论文。左侧为引导强度 1（无引导），右侧为引导强度度 3。

来自 OpenAI 的 GLIDE 模型的两组样本，提示为“一个舒适的客厅，沙发上方的墙上挂着柯基犬的画，沙发前有一张圆形咖啡桌，咖啡桌上放着一瓶鲜花。 '，取自他们的论文。左侧为引导强度 1（无引导），右侧为引导强度 3。

4、Reference

【1】：生成扩散模型漫谈（九）：条件控制生成结果
【2】：Improved Denoising Diffusion Probabilistic Models
【3】：https://sunlin-ai.github.io/2022/06/01/Classifier-Free-Diffusion.html
【4】：https://github.com/openai/glide-text2im
【5】：https://github.com/imesu2378/Glide-finetune