并查集(UnionFind)算法
并查集(UnionFind)算法
一、引入
问题:假设某个省中有N个城镇,有些城镇之间通过道路直接相连,有些则没有,如果城镇A与B有道路相连,B与C有道路相连,那么我们也可以从A走到C。现给出该省所有城镇的道路状况,判断是否可以从给定的某个城镇到达另一个城镇。
这个问题可以抽象为一个图论问题:给定一个无向图,判断图中某两点间是否连通。
对于这个问题,有多种方法可以解决,最容易想到的是DFS、BFS、Dijkstra算法等,但是,这几种算法的时间复杂度相对较高,如Dijkstra算法在堆优化后的时间复杂度为 O ( ( m + n ) log n ) O((m + n)\log{n}) O((m+n)logn)。
仔细观察这个问题,可以看到题中只要求判断两点间是否可达,没有要求找到可达路径。而上面所说的几种算法,再求两点是否可达的同时,也求出了从一点到另一点的路径。
有没有一种算法,能够以更低的时间复杂度得出我们想要的结果呢?
下面介绍另外一种算法:并查集算法。
二、并查集
并查集的本质是通过一个一维数组来维护一个森林。开始时森林中的每一个节点都是孤立的,各自形成一个树。之后,进行若干次的合并操作,每次合并将两个树合并为一个更大的树。
1. parent数组结构
并查集内部维护了一个parent数组,其大小为图的节点数量,parent[p] 的值为节点p的父节点。如果一个节点没有父节点,则规定 parent[p] = p 。
2. 并查集的相关操作
1)查找操作(find)
作用:找出给定节点所在树的根节点。
实现方法:按照parent数组向上寻找,直到parent[p] = p 为止。
伪代码:
find(p):
while parent[p] != p:
p = parent[p]
return p
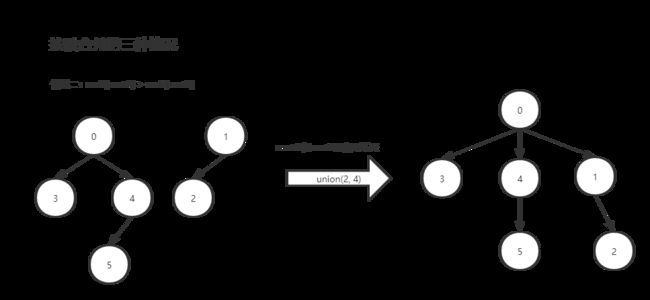
2)合并操作(union)
作用:将给定的两个节点所在的树进行合并,如果给定的两个节点已在同一个树中,则不进行任何操作。
实现方法:先通过find找到两个节点对应的根节点,然后让其中一个根节点成为另一个根节点的子节点即可。
union(a, b):
rootA = find(a)
rootB = find(b)
if rootA == rootB:
return
parent[rootA] = rootB # 或 parent[rootB] = rootA
3)判断两个节点是否连通
实现方法:如果这两个节点的根节点相同,则他们相连。
伪代码:
connected(a, b):
return find(a) == find(b)
自此,我们定义了一种新的数据结构:并查集。
下面给出该数据结构的具体实现:
python实现:
class UnionFind:
def __init__(self, n):
self.parent = [i for i in range(n)]
def find(self, p):
while self.parent[p] != p:
p = self.parent[p]
return p
def union(self, a, b):
rootA = self.find(a)
rootB = self.find(b)
if rootA == rootB:
return False
self.parent[rootA] = rootB
return True
def connected(self, a, b):
return self.find(a) == self.find(b)
java实现:
public class UnionFind {
private int[] parent;
public UnionFind(int n) {
this.parent = new int[n];
for (int i = 0; i < n; i++) {
this.parent[i] = i;
}
}
public boolean union(int a, int b) {
int rootA = find(a);
int rootB = find(b);
if (rootA == rootB) return false;
parent[rootA] = rootB;
return true;
}
private int find(int p) {
while (parent[p] != p) {
p = parent[p];
}
return p;
}
public boolean connected(int a, int b) {
return find(a) == find(b);
}
}
三、优化
1. 按秩合并
根据上面对并查集的分析,我们知道,并查集的find操作的时间复杂度与树的高度成正相关。所以,我们就有了一种优化的思路:尽可能的降低树的高度。
我们把以一个节点为根节点的树的高度叫做该节点的秩(rank)。
我们在并查集的内部维护一个rank数组,其中 rank[p] 的值表示节点p的秩。
初始化并查集时,rank数组中每一个下标对应的值都为1,因为此时还没有边的连接,所有节点各自形成一个树。
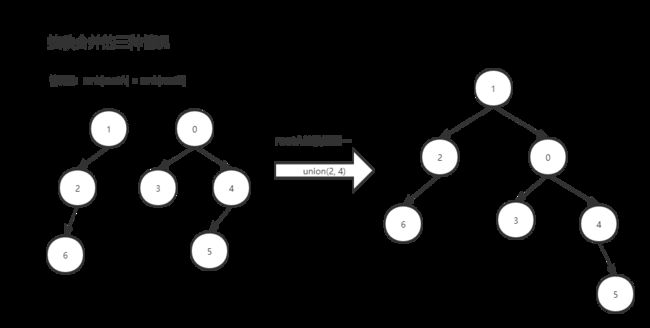
执行union操作时,我们先判断 rank[rootA] 和 rank[rootB] 的大小,如果rootA的秩小于rootB的秩,则将rootA的父节点设为rootB,此时rootA和rootB的秩均不变;否则,将rootB的父节点设为rootA,此时如果rootA的秩和rootB的秩相等,则rootA的秩需加一,否则rootA的秩不变。
修改后的union操作的伪代码:
union(a, b):
rootA = find(a)
rootB = find(b)
if rootA == rootB:
return False
if rank[rootA] < rank[rootB]:
parent[rootA] = rootB
else:
parent[rootB] = rootA
if rank[rootA] == rank[rootB]:
rank[rootA] += 1
return True
2. 路径压缩
即使使用了按秩合并的优化方法,随着合并操作次数的增加,形成的树的高度依然会增加。路径压缩优化的思想是在find操作查找根节点的过程中,将这个节点尽量的往上挪,以减少树的层数。
优化后的find操作的伪代码:
迭代实现:
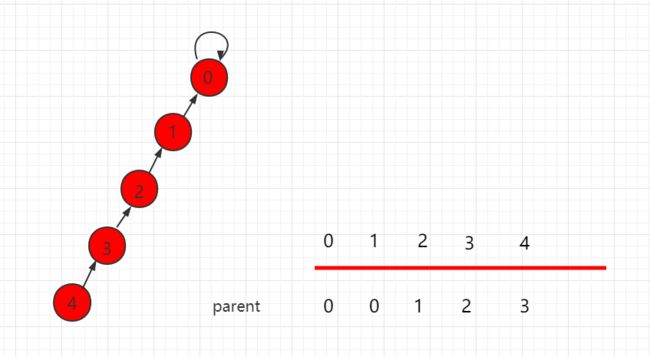
find(p):
while parent[p] != p:
parent[p] = parent[parent[p]]
p = parent[p]
return p
上述代码在查找根节点的同时会进行路径压缩操作:将该节点的父节点设为它原来的父节点的父节点。
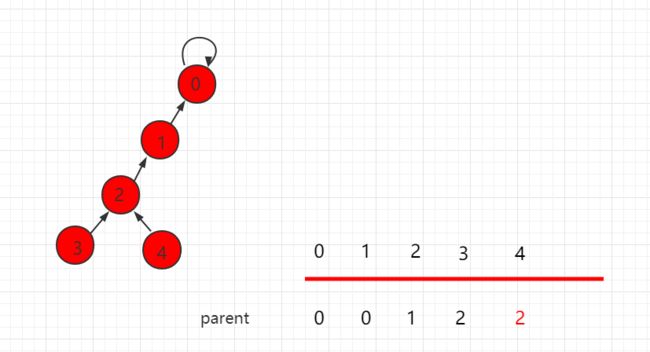
迭代实现的路径压缩过程:
由上图可知,迭代实现的压缩并不是最优压缩。实际上,我们可以通过递归来实现更有效的路径压缩方式。但要注意,当树的高度过大时,递归实现的压缩算法可能会出现爆栈的情况。
递归实现:
find(p):
if parent[p] != p:
parent[p] = find(parent[p])
return parent[p]
上述代码中,我们利用了递归的特性,将find操作时所“经过”的每一个节点都直接接在了它们对应的根节点上,从而达到了更有效的压缩。
通过这两种优化,我们得到了优化后的并查集。
下面给出优化后的并查集的具体实现:
python实现:
class UnionFind:
def __init__(self, n):
self.parent = [i for i in range(n)]
self.rank = [1 for _ in range(n)]
def find(self, p):
if self.parent[p] != p:
self.parent[p] = find(parent[p])
return parent[p]
def union(self, a, b):
rootA = self.find(a)
rootB = self.find(b)
if rootA == rootB:
return False
if self.rank[rootA] < self.rank[rootB]:
self.parent[rootA] = rootB
else:
self.parent[rootB] = rootA
if self.rank[rootA] == self.rank[rootB]:
self.rank[rootA] += 1
return True
def connected(self, a, b):
return self.find(a) == self.find(b)
java实现:
public class UnionFind {
private int[] parent;
private int[] rank;
public UnionFind(int n) {
this.parent = new int[n];
for (int i = 0; i < n; i++) {
this.parent[i] = i;
this.rank[i] = 1;
}
}
private int find(int p) {
if (parent[p] != p) {
parent[p] = find(parent[p]);
}
return parent[p];
}
public boolean union(int a, int b) {
int rootA = find(a);
int rootB = find(b);
if (rootA == rootB) return false;
if (rank[rootA] < rank[rootB])
parent[rootA] = rootB;
else {
parent[rootB] = rootA;
if (rank[rootA] == rank[rootB])
rank[rootA]++;
}
return true;
}
public boolean connected(int a, int b) {
return find(a) == find(b);
}
}
接下来,我们要通过并查集来解决我们一开始提出的问题。
四、复杂度分析
1. 空间复杂度:O(n)
2. 时间复杂度
| 优化 | 平均时间复杂度 | 最坏时间复杂度 |
|---|---|---|
| 无优化 | O ( log n ) O(\log{n}) O(logn) | O ( n ) O(n) O(n) |
| 路径压缩 | O ( α ( n ) ) O(\alpha(n)) O(α(n)) | O ( log n ) O(\log{n}) O(logn) |
| 按秩合并 | O ( log n ) O(\log{n}) O(logn) | O ( log n ) O(\log{n}) O(logn) |
| 路径压缩+按秩合并 | O ( α ( n ) ) O(\alpha(n)) O(α(n)) | O ( α ( n ) ) O(\alpha(n)) O(α(n)) |
证明:
这里只证明无优化和按秩合并优化的情况
在平均情况下,如果不使用「路径压缩」,那么当并查集最后仅包含 1棵树时,它的高度期望为 O ( log n ) O(\log{n}) O(logn)。在此基础上,如果我们使用「按秩合并」优化,就可以保证合并的有序性,是的最坏情况下连通分量的高度也为 O ( log n ) O(\log{n}) O(logn),即它是非常平衡的。如果我们不使用任何优化,那么最坏情况下会合并成一条链,那么每次查找代表元素就要遍历整条链,时间复杂度即为 O ( n ) O(n) O(n)。
由上表可知,通过上面两种优化后,并查集的查找和合并操作的平均时间复杂度已经可以接近于常数级别。
五、问题解决
- 创建出与给定图相同大小的并查集,此时并查集中无连接,parent[p] = p 恒成立。
- 遍历给定的无向图,如果图中的两个节点a、b存在边,则执行union(a, b)操作
- 判断给定的两个节点是否可达
六、拓展
并查集除了文中所说的求图中两点是否连通之外,还有其他用途。
1. 求无向图连通分量个数
通过对并查集的分析我们知道,如果图中两个点在同一个连通分量中,再在该图对应的并查集中,这两个点应该在同一个树中。由此可知,并查集中树的个数即为它对应的图的连通分量个数。
进一步分析,并查集每进行一次成功的union操作,都会使森林中原有的两棵树合并,即树的总数减一。
因此,我们在并查集内部维护一个变量count,用来记录连通分量的个数,初始化时 count = n,在每次成功的union操作后使count - 1。所有的合并操作完成之后count的值即为图的连通分量数目。
2. 判断图中是否存在环
并查集的另一个应用时判断图中是否存在环。由上面的分析我们知道,图中的每一条边都对应了并查集中的一次union操作,如果在构建一个图对应的并查集时,某一次union操作失败了(union方法返回了False),则说明这条边是一条“多余”的边,即这条边连接的两个顶点在添加这条边之前已经连通了,此时如果再加上这条边就形成了一个环。
因此,我们通过观察并查集构建过程中是否有失败的union操作,即可判断图中是否有环。