leetcode 剑指 Offer 14- II. 剪绳子
- 题目描述
- 解题思路
- 执行结果
题目描述
给你一根长度为 n 的绳子,请把绳子剪成整数长度的 m 段(m、n都是整数,n>1并且m>1),每段绳子的长度记为 k[0],k[1]...k[m - 1] 。请问 k[0]k[1]...*k[m - 1] 可能的最大乘积是多少?例如,当绳子的长度是8时,我们把它剪成长度分别为2、3、3的三段,此时得到的最大乘积是18。
答案需要取模 1e9+7(1000000007),如计算初始结果为:1000000008,请返回 1。
示例 1:
输入: 2 输出: 1 解释: 2 = 1 + 1, 1 × 1 = 1 示例 2:
输入: 10 输出: 36 解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36
提示:
2 <= n <= 1000
来源:力扣(LeetCode) 链接:https://leetcode.cn/problems/jian-sheng-zi-ii-lcof 著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
解题思路
与第一题类似,不同的是数据的范围增大了,所以原本的解决方法就不能用了 我们需要自己写求幂的方法,同时需要对计算值进行取余1000000007以保证数据不会溢出
法1
- 时间复杂度(O(n))
- 空间复杂度(O(1))
法2
快速幂算法 简单来讲就是当我们计算x^n时可以不用一个个进行xx
比如x^2=xx
x^4=x^2x^2
x^8=x^4x^4
因为我们前面以及计算过值,就可以将值直接拿来用就可以了, 我们将n表示成二进制的形式,出现1的位置就是要计算值的位置,这样可以优化时间复杂度
- 时间复杂度(O(logn))
- 空间复杂度(O(1))
法3
- 时间复杂度(O())
- 空间复杂度(O())
执行结果
法1
func cuttingRope(n int) int {
if n < 4 {
return n - 1
}
r := 1
for i := 0; i < n/3-1; i++ {
r = (r * 3) % 1000000007
}
if n%3 == 1 {
return (r * 4) % 1000000007
}
if n%3 == 2 {
return (r * 6)% 1000000007
}
return r*3% 1000000007
}
题目描述 评论 (530) 题解 (762) 提交记录 执行结果: 通过 显示详情 查看示例代码 添加备注
执行用时: 0 ms , 在所有 Go 提交中击败了 100.00% 的用户 内存消耗: 1.7 MB , 在所有 Go 提交中击败了 94.55% 的用户 通过测试用例: 55 / 55
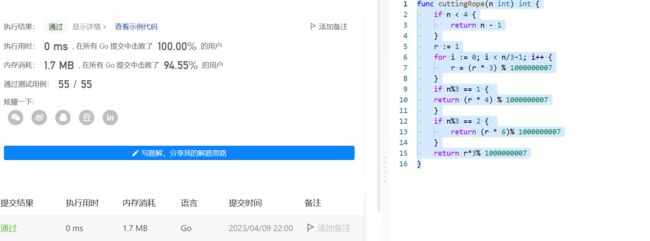
法2
//快速幂
func cuttingRope(n int) int {
if n <= 3 {
return n - 1
}
a := n / 3
b := n % 3
if b == 0 {
return pow(3, a, 1000000007)
} else if b == 1 {
return (pow(3, a-1, 1000000007) * 4) % 1000000007
} else {
return (pow(3, a, 1000000007) * 2) % 1000000007
}
}
//快速幂算法
func pow(x, n, mod int) int {
res := 1
for n > 0 {
if n&1 == 1 {
res = (res * x) % mod
}
x = (x * x) % mod
n >>= 1
}
return res
}
执行结果: 通过 显示详情 查看示例代码 添加备注
执行用时: 0 ms , 在所有 Go 提交中击败了 100.00% 的用户 内存消耗: 1.8 MB , 在所有 Go 提交中击败了 43.58% 的用户 通过测试用例: 55 / 55 炫耀一下:
本文由 mdnice 多平台发布