python 实现数据结构八种内部排序算法
目录
一、插入排序
二、希尔排序
三、冒泡排序
四、快速排序
五、选择排序
六、堆排序
七、归并排序
八、基数排序
一、插入排序
array_test = [8,3,5,1,10,4,2,6,7,9]
# 插入排序
# 将数组分为“已排序好”“未排序”两部分
# 每次循环依次从“未排序”中拿出一个 插入到“已排序好”的合适位置
def InsertSort(array):
for i in range(1,len(array)): # 默认0号位置已经排好
if array[i] < array[i-1]: # 如果比已排序好的列表最大的元素还大 就不需要比较
temp = array[i]
# 思路:将temp放到合适位置 并将temp后的元素向后移
j = i-1
k = i
# 找到temp的合适位置
while array[j] > temp and j >= 0:
j = j - 1
# 注意此时j指向的是待插入元素的前一个位置
# 所以不能移动array[j] 从后到前移动到array[j+1]
while k > j+1:
array[k] = array[k-1]
k = k - 1
# 把temp放进来
array[j+1] = temp
return array
print(InsertSort(array_test))空间复杂度:O(1)
最好时间复杂度:O(n) 数组原来就有序,只需要每次比较,不需要移动
最坏时间复杂度:O(n)
平均时间复杂度:O(n²)
稳定性:稳定
折半插入排序:在寻找插入位置时,通过改用折半查找以减少比较次数,提升效率:
def InsertSort(array):
for i in range(1,len(array)): # 默认0号位置已经排好
if array[i] < array[i-1]: # 如果比已排序好的列表最大的元素还大 就不需要比较
temp = array[i]
# 思路:将temp放到合适位置 并将temp后的元素向后移
high = i-1
low = 0
k = i
# 找到temp的合适位置
while low <= high:
mid = (low+high)/2
if array[mid] > temp:
high = mid - 1
else:
low = mid + 1
# 注意此时j多减了1 已经是temp之前的位置
# 把合适位置后的所有元素向后移位时 j要加一
while k > high+1:
array[k] = array[k-1]
k = k - 1
# 把temp放进来
array[high+1] = temp
return array在代码中,我们需要注意的是二分查找进行了一点小改动,取消了array[mid] == temp的情况,这是因为即时二者相等,出于排序算法稳定性的考虑,我们希望“原本位置靠后的元素”仍可以排在“值相等、但原本靠前的元素”之后。
折半插入排序优化了比较时间复杂度(O(nlogn)),但由于其移动的时间复杂度仍为O(n²),故其总的时间复杂度为O(n²)。
二、希尔排序
array_test = [8, 3, 5, 1, 10, 4, 2, 6, 7, 9]
# 希尔排序
# 希尔排序是基于“插入排序对有序表/基本有序表效率高”产生的
# 先追求部分有序 再追求全局有序
# 排序增量为d的子表[i,i+d,i+2d...] 不断缩小增量d
def ShellSort(array):
d = len(array)//2
while d >= 1:
for i in range(d, len(array)):
if array[i] < array[i-d]: # 则需要将array[i]插入有序子表
# 插入排序
temp = array[i]
j = i - 1
k = i
while array[j] > temp and j >= 0:
j = j - 1
while k > j + 1:
array[k] = array[k - 1]
k = k - 1
array[j + 1] = temp
d = d//2 # 步长折半
return array
print(ShellSort(array_test))d=1时,即为对一个基本有序的序列进行插入排序。
空间复杂度:O(1)
时间复杂度:还不能由数学推导
稳定性:不稳定
三、冒泡排序
array_test = [8, 3, 5, 1, 10, 4, 2, 6, 7, 9]
# 冒泡排序
# 从后向前依次对比 每一轮都把最小的放在最前面
# 一共需要进行n-1次
def swap(i,j):
return j,i
def BubbleSort(array):
n = len(array)
for i in range(0, n-1):
j = n-1
while j > i:
if array[j] < array[j-1]:
array[j],array[j-1] = swap(array[j],array[j-1])
j = j - 1
return array
print(BubbleSort(array_test))“完全版”的冒泡排序会设立一个flag标记,当某次比较并没有发生元素移动时,则停止下一轮比较,提前结束排序。
空间复杂度:O(1)
最好时间复杂度:O(n)
最坏时间复杂度:O(n²)
平均时间复杂度:O(n²)
稳定性:稳定
四、快速排序
array_test = [8, 3, 5, 1, 10, 4, 2, 6, 7, 9]
# 快速排序
# 每次选择一个元素作为基准 将表“划分”为左右两个部分
# 递归的对子表选择基准 进行划分
def QuickSort(array,low,high):
if low < high: # 递归终止条件
# low == high 的时候即为划分后为两个元素的情况
pivotpos = Partition(array,low,high)
QuickSort(array,low,pivotpos-1)
QuickSort(array, pivotpos+1,high)
return array
def Partition(array,low,high):
privot = array[low] # 第一个元素作为privot
# 因为已经用privot保存了第一个元素的值 所以可以将low指针指向的位置视为空
while low < high:
# 此时,可以将low指针指向的位置视为空
# 先移动high指针
while low < high and array[high] >= privot:
high = high - 1
array[low] = array[high] # 比privot小的放左边
# 此时,可以将high指针指向的位置视为空
while low < high and array[low] <= privot:
low = low + 1
array[high] = array[low] # 比privot大的放右边
array[low] = privot # 此时low == high 将privot元素放置于此
return low # 返回存放privot的位置
print(QuickSort(array_test,0,len(array_test)-1))快速排序递归调用的层数就是二叉树的高度。
最好空间复杂度:O(logn)
最坏空间复杂度:O(n)
最好时间复杂度:O(nlogn)
最坏时间复杂度:O(n²)
稳定性:不稳定
五、选择排序
array_test = [8, 3, 5, 1, 10, 4, 2, 6, 7, 9]
# 选择排序
# 从左向右 每次选择最小的值,放到未排序序列的首部
# 一共需要n-1次
def swap(i,j):
return j,i
def SelectSort(array):
n = len(array)
for i in range(0,n-1):
min_pos = i # 记录最小元素位置
for j in range(i+1,n):
if array[j]空间复杂度:O(1)
时间复杂度:O(n²)
稳定性:不稳定
六、堆排序
array_test = [8, 3, 5, 1, 10, 4, 2, 6, 7, 9]
# 堆排序
# 建立大根堆
# 将堆顶元素和待排序序列中的最后一个交换
# 将剩余的[0,n-i]个元素调整为大根堆
def swap(i, j):
return j, i
# 将k为根结点的树 调整为大根堆
def HeadAjust(array, k, len):
temp = array[k] # 保存要判断的结点 直到下降到满足大根堆的位置
i = 2*k # 左孩子
while i < len: # 存在左孩子
if i+1 < len and array[i] < array[i+1]: # 存在右孩子
# 比较左右孩子的大小
i = i + 1
# 若以该结点为根节点的树不是最大堆,以上操作已经找到了应该成为根节点的孩子
if temp >= array[i]: # 如果已经满足了最大堆
break
else:
array[k] = array[i] # 与较大子树的值交换
# 小元素逐层下坠
k = i # 此时还不能直接完成交换 仍要继续向下比较
i = i * 2
array[k] = temp
# 建立大根堆
def BuildMaxHeap(array,len):
# 只需要处理非叶结点
k = len // 2 # 一颗完全二叉树的叶子结点数为 n/2向上取整
while k >= 0:
HeadAjust(array, k, len)
k = k - 1 # 自底向上调整
# 堆排序
def HeapSort(array):
n = len(array)
# 建立大根堆
BuildMaxHeap(array, n)
# 指向待排序数组的最后位置
i = n-1
while i > 0:
array[i], array[0] = swap(array[i], array[0])
# 将根节点为0的调整为大根堆 即选出了数组中最大的元素 放到array[i]的位置
HeadAjust(array, 0, i-1)
# 每次待排序的长度都减一
i = i - 1
return array
print(HeapSort(array_test))建堆:O(n)
排序:O(nlogn)
总时间复杂度:O(nlogn)
稳定性:不稳定
七、归并排序
array_test = [8, 3, 5, 1, 10, 4, 2, 6, 7, 9]
# 归并排序
# 合并两个有序数组的操作 Merge
def Merge(array,low,mid,high):
# 必须要分配空间 若直接temp = [] 则temp[k]会报错
temp = [0] * (high+1)
# 将原数组复制到temp中
for k in range(low, high+1):
temp[k] = array[k]
i = low
j = mid+1
k = i
# 合并过程
while i <= mid and j <= high:
if temp[i] <= temp[j]:
array[k] = temp[i]
i = i + 1
else:
array[k] = temp[j]
j = j + 1
k = k + 1
# 处理没有合并完的子序列
while i <= mid:
array[k] = temp[i]
k = k + 1
i = i + 1
while j <= high:
array[k] = temp[j]
k = k + 1
j = j + 1
def MergeSort(array,low,high):
if low < high:
mid = (low+high)//2
# 归并排序左半边
MergeSort(array, low, mid)
# 归并排序右半边
MergeSort(array, mid+1, high)
# 合并
Merge(array, low, mid, high)
return array
print(MergeSort(array_test, 0, len(array_test)-1))
空间复杂度:O(n) 辅助数组(递归工作栈复杂度O(logn))
时间复杂度:O(nlogn)
稳定性:稳定
八、基数排序
把关键词拆分为 d 位,按照关键字权重递增的顺序进行d躺分配、收集。
需要建立r个辅助队列
空间复杂度:O(r)
分配时,对于某一位,只需要从头到尾把元素扫一遍,n位的时间为 d*n
收集时,由于只需要改变一次链表的指针,对每个队列的操作时间为O(1),时间为为d*r
时间复杂度: O(d(n+r))
稳定性:稳定
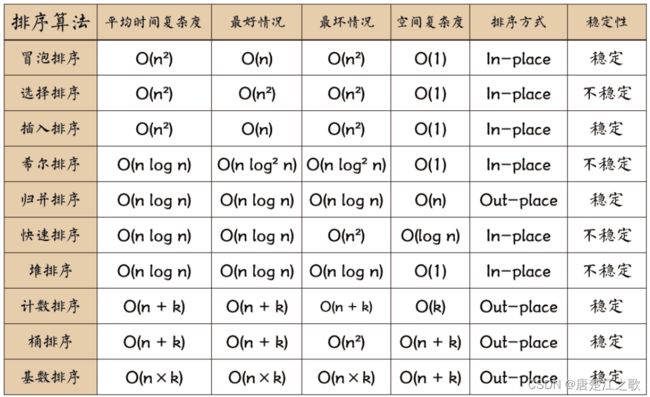
总结:
1、(图片来自于python菜鸟教程 侵删)
2、
元素的移动次数与关键字的初始排列次序无关的是:基数排序
元素的比较次数与初始序列无关是:选择排序、折半插入排序
算法的排序趟数与初始序列无关的是:插入排序、选择排序、基数排序
算法的时间复杂度与初始序列无关的是:选择排序、堆排序、归并排序、基数排序
记忆方法:一堆(堆排序)乌龟(归并)选(选择)基(基数)佬
这个记忆方法来自于CSDN博主 @寒泉Hq