二叉树遍历DFS BFS

（DFS）二叉树深度搜索的三种遍历方式：先序遍历、中序遍历和后序遍历的递归和迭代

递归实现：先序遍历、中序遍历和后序遍历

先序遍历：

void preorderTra(TreeNode* root, vector<int>& nodes) {
    if (root == nullptr) {
        return;
    }
    node.push_back(root->val);
    preorderTra(root->left, nodes);
    preorderTra(root->right, nodes);
}

中序遍历

void inorderTra(TreeNode* root, vector<int>& nodes) {
    if (root == nullptr) {
        return;
    }
    inorderTra(root->left, nodes);
    node.push_back(root->val);
    inorderTra(root->right, nodes);
}

后序遍历

void postorderTra(TreeNode* root, vector<int>& nodes) {
    if (root == nullptr) {
        return;
    }
    postorderTra(root->left, nodes);
    postorderTra(root->right, nodes);
    node.push_back(root->val);
}

迭代实现：先序遍历、中序遍历和后序遍历

先序遍历：

void preorderTra(TreeNode* root, vector<int>& nodes) {
    stack<TreeNode*> sta;
    TreeNode* cur = root;
    while (cur != nullptr || !sta.empty()) {
        while (cur != nullptr) {
            //处理根
            nodes.push_back(cur->val);
            //入栈
            sta.push(cur);
            //向左走
            cur = cur->left;
        }
        //出栈
        cur = sta.top();
        sta.pop();
        //向右走
        cur = cur->right;
    }
}

中序遍历

void inorderTra(TreeNode* root, vector<int>& nodes) {
    stack<TreeNode*> sta;
    TreeNode* cur = root;
    while (cur != nullptr || !sta.empty()) {
        while (cur != nullptr) {
            //入栈
            sta.push(cur);
            //向左走
            cur = cur->left;
        }
        //出栈
        cur = sta.top();
        sta.pop();
        //处理根节点
        nodes.push_back(cur->val);
        //向右走
        cur = cur->right;
    }
}

后序遍历

void postorderTra(TreeNode* root, vector<int>& nodes) {
    stack<TreeNode*> sta;
    TreeNode* cur = root;
    TreeNode* prev = nullptr;//标记作用
    while (cur != nullptr || !sta.empty()) {
        while (cur != nullptr) {
            sta.push(cur);
            cur = cur->left;
        }
        //判断当前节点是否有右
        //有 处理
        cur = sta.top();
        if (cur->right != nullptr && cur->right != prev) {
            cur = cur->right;
        //没有 出栈
        } else {
            sta.pop();
            nodes.push_back(cur->val);
            prev = cur;
            cur = nullptr;
        }   
    }
}

(BFS)二叉树的层次遍历-剑指 Offer II 043 044 045 046

二叉树的层次遍历实现步骤：

1.定义队列queue存储树的节点
2.根节点入队列
3.当数组不为空时，遍历数组（提前确定队列queue的最大值）
4.获取队列头节点
5.将当前节点的子节点加入队列中

剑指 Offer II 043. 往完全二叉树添加节点

c++实现

class CBTInserter {
private:
    queue<TreeNode*> que;
    TreeNode* root;
public:
    //构建树
    CBTInserter(TreeNode* root) {
        this->root = root;
        //根节点进入队列
        que.push(root);
        while(que.front()->left != nullptr && que.front()->right != nullptr){
            que.push(que.front()->left);
            que.push(que.front()->right);
            que.pop();
        }
    }
    
    int insert(int v) {
        //定义要插入的节点
        TreeNode* node =new TreeNode(v);
        //标记指向头节点
        TreeNode* fa = que.front();
        if(fa->left == nullptr){
            fa->left = node;
        }
        else{
            fa->right = node;
            //当根节点为左右节点都有时，将左右节点入队列，根节点出队列
            que.push(fa->left);
            que.push(fa->right);
            que.pop();
        }
        return fa->val;
    }
    
    TreeNode* get_root() {
        return this->root;
    }
};

golang实现

type CBTInserter struct {
    root *TreeNode
    queue  []*TreeNode
}

func Constructor(root *TreeNode) CBTInserter {
    //判断根节点是否为空
    if root == nil {
		return CBTInserter{nil,[]*TreeNode{}}
	}
    //go没有类 所有需要声明数组变量
    var queue []*TreeNode 
    //将根节点加入队列
    queue = append(queue,root)
    for len(queue)>0 {
        node := queue[0]
        if node.Left != nil {
            queue = append(queue,node.Left)
        }else{
            break
        }
        if node.Right != nil {
            queue = append(queue,node.Right)
        }else{
            break
        }
        queue = queue[1:]
    }
    return CBTInserter{root,queue}
}

func (this *CBTInserter) Insert(v int) int {
    //标记头节点
    var parentVal int
    parentVal = this.queue[0].Val
    node := &TreeNode{Val:v}
    this.queue = append(this.queue,node)
    if this.queue[0].Left == nil {
        this.queue[0].Left = node
    }else{
        this.queue[0].Right = node
        this.queue=this.queue[1:]
    }
    return  parentVal//必须定义 不能直接返回this.queue[0].Val 因为上面已经this.queue=this.queue[1:]
}

func (this *CBTInserter) Get_root() *TreeNode {
    return this.root
}

剑指 Offer II 044. 二叉树每层的最大值

给定一棵二叉树的根节点 root ，请找出该二叉树中每一层的最大值。


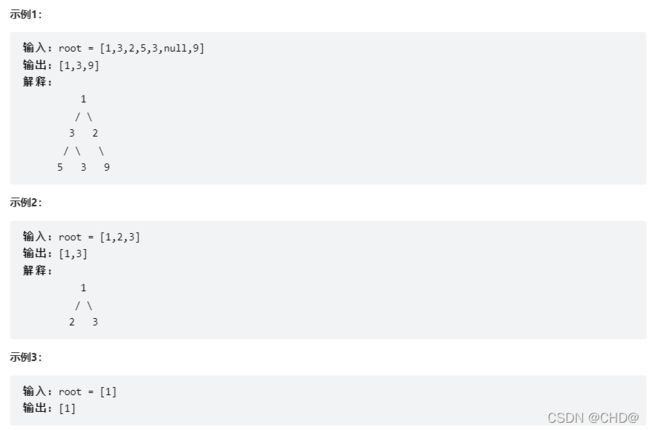
实现步骤：

1.空根节点的判断
2.定义向量容器存储最大值的集合
3.定义队列存储树的节点
4.根节点入队列
5.遍历数组
6.获取队列头节点
7.更新最大值
8.将当前节点的子节点加入队列中
9.将每层的最大值加入到向量容器中
10.返回最大数组

c++实现：

class Solution {
public:
    vector<int> largestValues(TreeNode* root) {
        //空根节点的判断
        if (root == nullptr){
            return {};
        }
        vector<int> allmax;
        queue<TreeNode*> que;
        //根节点入队列
        que.push(root);
        while(!que.empty()){
            //size 必须在进入 for 循环前就确定，而不是使用 que.size()，因为队列大小实时在改变。
            int size = que.size();
            int curmax = INT_MIN;//int类型最小值
            for (int i = 0; i < size; i++){
                //获取队列头节点
                TreeNode* node = que.front();
                que.pop();
                //更新最大值
                curmax = max(curmax,node->val);
                //将当前节点的子节点加入队列中
                if(node->left != nullptr){
                    que.push(node->left);
                }
                if(node->right != nullptr){
                    que.push(node->right);
                }
            }
            //加入到最大向量组中
            allmax.push_back(curmax);
        }
        return allmax;
    }
};

golang实现

/**
 * Definition for a binary tree node.
 * type TreeNode struct {
 *     Val int
 *     Left *TreeNode
 *     Right *TreeNode
 * }
 */
func largestValues(root *TreeNode) []int {
    if root == nil {
        return []int{}
    }
    var allmax []int
    var queue []*TreeNode
    queue = append(queue,root)
    for len(queue)>0 {
        size := len(queue)
        var curmax int = math.MinInt32//32位的整数范围的最小值
        for i:=0;i<size;i++ {
            node := queue[0];
            queue = queue[1:]
            curmax = max(curmax,node.Val)
            if node.Left != nil {
                queue = append(queue,node.Left)
            }
            if node.Right != nil {
                queue = append(queue,node.Right)
            }
        }
        allmax = append(allmax,curmax)
    }
    return allmax
}

func max(a,b int) int {
    if a>b {
        return a
    } 
    return b
}

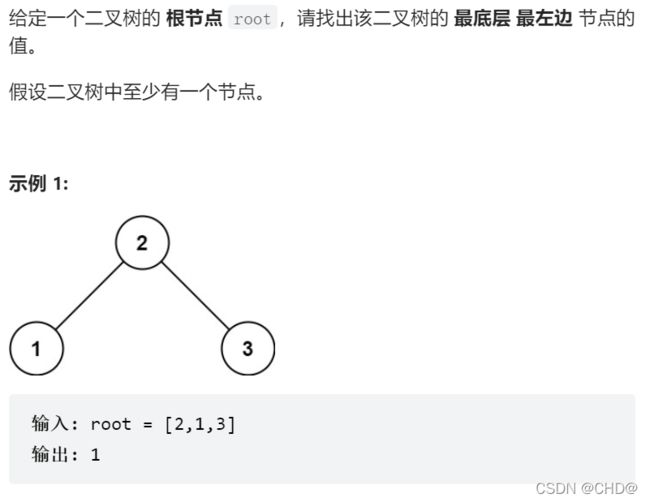
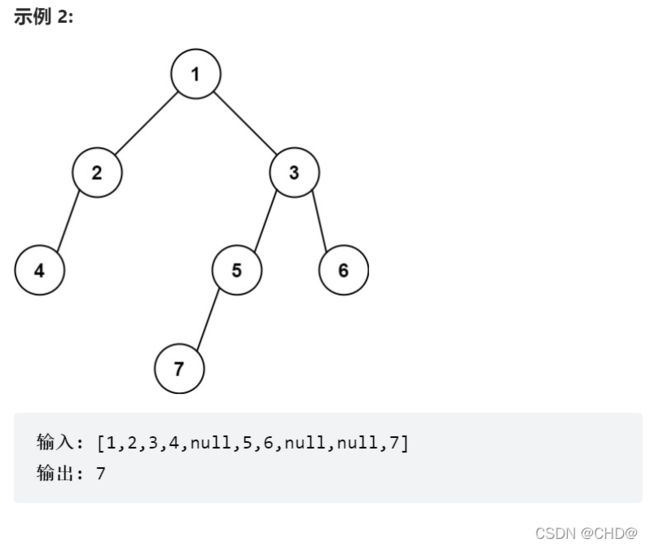
剑指 Offer II 045. 二叉树最底层最左边的值

c++实现

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int findBottomLeftValue(TreeNode* root) {
        queue<TreeNode*> que;
        que.push(root);
        int bottomleft;
        while(!que.empty()){
            int size = que.size();//que的大小要提前确定，que.size()是变化的，不是固定的。
            for(int i=0;i<size;i++){
                TreeNode* node = que.front();
                que.pop();
                //更新树的最左边的值  
                if(i==0){
                    bottomleft = node->val;
                }
                if(node->left != nullptr){
                    que.push(node->left);
                }
                if(node->right != nullptr){
                    que.push(node->right);
                }
            }
        }
        return bottomleft;
    }
};

golang实现

func findBottomLeftValue(root *TreeNode) int {
    var queue[]*TreeNode
    queue = append(queue,root)
    var bottomleft int
    for len(queue)>0 {
        size := len(queue)
        for i:=0;i<size;i++ {
            node := queue[0]
            queue = queue[1:]
            if i == 0 {
                bottomleft = node.Val
            }
            if node.Left != nil {
                queue=append(queue,node.Left)
            }
            if node.Right != nil {
                queue=append(queue,node.Right)
            }
        }
    }
    return bottomleft
}

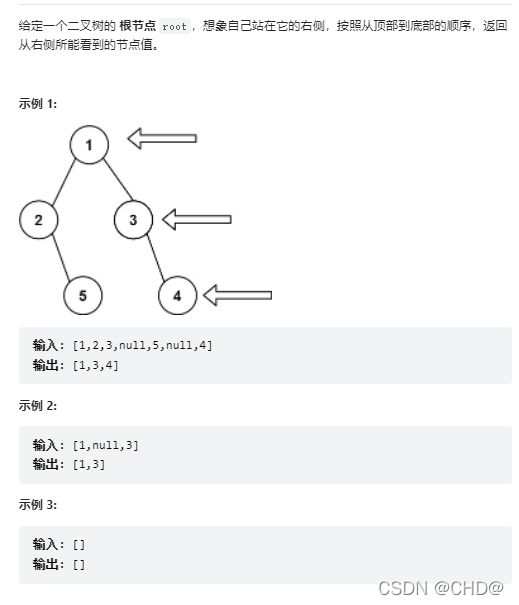
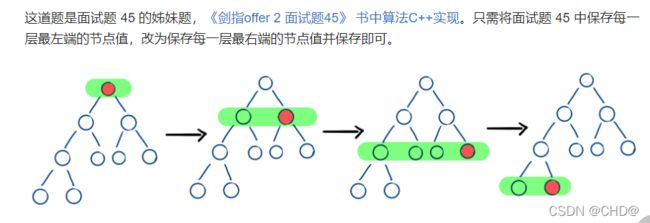
剑指 Offer II 046. 二叉树的右侧视图

思路：

c++实现：

class Solution {
public:
    vector<int> rightSideView(TreeNode* root) {
        if(root == nullptr){
            return {};
        }
        queue<TreeNode*> que;
        vector<int> rightSide;
        que.push(root);
        while(!que.empty())
        {
            int size = que.size();
            for(int i=0;i<size;i++)
            {
                TreeNode* node = que.front();
                que.pop();
                if(i == size-1)
                {
                    rightSide.push_back(node->val);
                }
                if(node->left != nullptr)
                {
                    que.push(node->left);
                }
                if(node->right != nullptr)
                {
                    que.push(node->right);
                }
            }
        }
        return rightSide;
    }
};

golang实现

func rightSideView(root *TreeNode) []int {
    if root==nil {
        return []int{}
    }
    var queue []*TreeNode
    var view []int
    queue = append(queue,root)
    for len(queue)>0 {
        size := len(queue)
        for i:=0;i<size;i++ {
            node := queue[0]
            queue = queue[1:]
            if i==(size-1) {
                view = append(view,node.Val)
            }
            if node.Left != nil {
                queue=append(queue,node.Left)
            }
            if node.Right != nil {
                queue=append(queue,node.Right)
            }
        }
    }
    return view
}