【三重卷积神经网络:TDNet:PanSharpening】

A Triple-Double Convolutional Neural Network for Panchromatic Sharpening

（一种用于全色锐化的三重卷积神经网络）
全色锐化是指将具有高空间分辨率的全色图像与具有低空间分辨率的多光谱图像进行融合，以获得高空间分辨率的多光谱图像。在这篇文章中，我们提出了一种新的深度神经网络结构，其基于水平域的损失函数用于全色锐化，并考虑了以下两种类型的结构，即两级、双支、双向，称为三重网络（TDNet）。利用TDNet的结构，可以充分挖掘和利用全色图像的空间细节，逐步注入到低空间分辨率的多光谱图像中，从而获得高空间分辨率的输出。具体的网络设计是由传统的多分辨率分析（MRA）方法的物理公式驱动的。因此，有效的MRA融合模块也被集成到TDNet中。此外，采用少量的ResNet模块和多尺度卷积核对网络进行深化和扩展，有效地提高了TDNet的特征提取能力和鲁棒性。在WorldView-3、QuickBird和Gaofen-2传感器采集的降分辨率和全分辨率数据集上进行的大量实验表明，与一些最新的全色锐化方法相比，本文提出的TDNet具有优越性。

介绍

遥感卫星专门用于从地球表面收集图像数据。然而，由于传感器硬件信噪比（SNR）的一些限制，我们无法在唯一采集中获得高空间和光谱分辨率。因此，诸如IKONOS、GaoFen、QuickBird和WorldView-3的卫星通常捕获包含多个光谱带的图像，称为多光谱（MS）图像，以及具有高空间分辨率的全色（PAN）图像，即包含许多图像细节。因此，通常需要融合这些类型的数据以获得非常高的空间-光谱分辨率产品。全色锐化是PAN图像和MS图像的融合，以获得具有与PAN图像相同的空间分辨率和与MS图像相同的光谱分辨率的最终结果。这一研究课题近年来发展迅速，并被证明是一种有效的图像融合方法。全色锐化的结果已广泛用于地面目标检测、制图和各种高级应用的图像数据预处理。
在过去的几十年中，针对全色锐化问题已经提出了许多不同的方法，并且这些技术可以大致分为四类，即，分量替换（CS）方法、多分辨率分析（MRA）方法、变分优化（VO）方法和深度学习（DL）技术。在本文中，我们的方法是基于卷积神经网络（CNN），因此属于DL技术。在下文中，我们将介绍每个类别的代表性方法。
基于CS的方法通常是属于传统技术的简单方法。它们将原始MS图像投影到变换域中，其目的是简化部分或全部空间信息的替换，使得更容易用PAN图像替换空间结构分量。值得一提的是，许多开创性的全色锐化方法是基于CS哲学的，因为这类方法通常具有简单和有效的实现。这类中的一些代表性示例是部分替换自适应CS（PRACS）、Gram-Schmidt（GS）频谱锐化和具有局部参数估计的带相关空间细节（BDSD）。请注意，基于CS的方法通常可以获得具有更好渲染的产品，但会产生更大的频谱失真。
MRA方法是另一类传统方法，其目标是将从PAN图像提取的空间细节注入到MS图像中，MS图像被内插到PAN图像的大小。在光谱质量方面，基于MRA的融合结果上级基于CS的融合结果。然而，这些方法容易产生伪影，因此经常引入空间失真。属于这类的一些方法例如是基于平滑滤波器的强度调制（SFIM），加性小波亮度比例（AWLP），具有高通调制注入模型的调制传递函数广义拉普拉斯金字塔（GLP-HPM），以及调制传递函数广义拉普拉斯金字塔与基于全分辨率回归的注入模型（GLPReg）。
与上述传统方法不同，基于VO的方法是通过施加预先指定的先验项来正则化基础高分辨率多光谱（HRMS）图像而开发的。这些方法显示了优雅的数学公式，并且与一些最先进的CS和MRA技术相比，在空间-频谱保存方面具有良好的性能。基于VO方法的主要缺点是计算量大，包括许多超参数的调整。因此，CS和MRA方法现在仍然用于基准测试目的。
近年来，深度学习技术因其能够从大数据中隐式学习先验知识的强大能力而备受关注。毫无疑问，基于深度学习的方法已经广泛应用于遥感图像领域。深度学习作为一个新发展起来的解决泛化的范畴，需要更高层次的物理支撑。结构设计是至关重要的，因为它与模型的性能增益密切相关。通过构建具有一定结构和功能单元的卷积神经网络（CNN），（例如，深度残差网络、多尺度多深度网络），DL方法可以通过对卫星数据集的训练来再现MS图像、PAN图像和理想融合图像之间的非线性关系。Masi等人在2016年进行了突破性的尝试，使用了专门为全色锐化设计的三层CNN，取得了令人鼓舞的结果。受PNN的启发，许多研究人员开发了各种依赖于CNN的结构。其中，ResNet中的残差模块被广泛用于全色锐化。然而，神经网络的学习过程很难解释，当参数难以更新时，神经网络常常陷入梯度消失的困境。特别是图像的一些本质属性和先验信息，如高频信息的唯一性、频谱的内在联系等，往往被这类“黑箱”深度模型所忽略，留下了很大的改进空间。因此，我们认为，网络框架的设计应基于手头的问题的一些特点，强调输入图像之间的独特关系。
本文提出了一种新的DL全色锐化方法，该方法利用多尺度空间细节策略，逐步将PAN细节注入低分辨率MS图像。基于MRA公式设计了一种新型的三重-双重网络（TDNet）结构。

贡献

1）提出了一种双层、双分支、双向的网络总体结构，将PAN图像潜在的多尺度空间细节分层次、双向地注入到MS图像中。在此框架下，采用基于层次域的损失函数对多层次结果进行约束，保证了最终融合结果的合理性。
2）遵循传统的MRA方法，设计了一种嵌入TDNet结构的MRA模块（MRAB）。MRAB能较好地完成PAN图像结构信息的提取。这种分块结构的设计还引入了注意机制的思想，比传统的方法更灵活、鲁棒。
3）考虑到全色化问题需要在不同尺度上注入不同的对象，采用多尺度卷积核模块对网络进行深化和扩展，提高了网络的非线性拟合能力。图1所示的结果证明了该方法的优越性。

NOTATION AND RELATED WORKS

Notation

为方便起见，首先介绍本文中使用的符号。低分辨率多光谱（LRMS）图像和高分辨率全色（PAN）图像分别表示为MS ∈ $R^{h\times w\times c}$和P ∈ $R^{H\times W}$。所需的高分辨率多光谱（HRMS）图像定义为^MS ∈ $R^{H\times W\times c}$。在PAN图像尺度上采样的多光谱图像表示为~ MS ∈ $R^{H\times W\times c}$，而地面真实图像表示为GT ∈$R^{H\times W\times c}$。

Background

由于硬件设备的限制，仅采集LRMS和PAN图像。考虑到全色锐化的目标是生成具有高空间分辨率的多光谱图像，一般的融合公式可以总结如下，

其中F_θ（·）用于描述所涉及图像之间的潜在关系。许多全色锐化方法（传统的和基于DL的）背后的共同思想是找到合适的方式来表征已知LRMS和PAN图像与期望的HRMS图像之间的关系。

Overview of MRA Methods

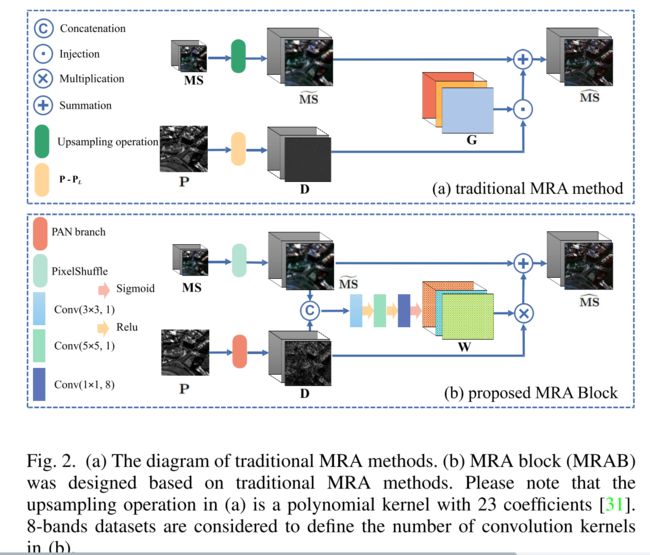
传统的MRA方法在全色锐化方面具有竞争力。一般MRA方法示意图如图2（a）所示。可以看出，MRA方法具有两个主要过程，即：从PAN图像P中提取空间结构细节，并通过某些策略将从P中获得的信息注入到~ MS中。MRA方法的数学公式由下式给出：在（2）中，空间结构可以通过差值P−P_L获得，其中PL可以通过不同的滤波器获得。相关文献还提出了关于细节注入过程的各种尝试。传统的MRA方法虽然能够保留频谱信息，但可能会引入空间失真。

CNNs for Pansharpening

在DL全色锐化方法中，基于神经网络的方法由于其在特征提取阶段的出色能力而得到了深入的研究。解决全色锐化问题的现有基于CNN的框架可以通过最小化以下损失函数来粗略地概括：

用于全色锐化的基本结构可以表示如下，
基于上述策略，人们提出了许多有效的、有前途的神经网络来完成全色锐化任务。Masi等人提出了一种通过简单的三层卷积映射关系的改进的超分辨率网络。另一个典型的例子是Yang等人提出的PanNet。它考虑了高通特征的光谱和空间保真度，并引入了ResNet结构来深化给定的网络。Yuan等人提出使用多尺度卷积核来提取不同图像尺度上的特征，与单尺度卷积核相比，获得了满意的结果。不同于将P和MS一起馈送到网络中，Zhang等人提出了一种称为BDPN的新颖网络架构，其中通过利用双向金字塔结构，使用不同分支来处理P和MS。

Motivation

虽然各种基于CNN的方法已经取得了有希望的结果，但是仍然存在改进的空间，例如，物理上可解释的体系结构、多尺度结构的使用等等。最近，不同于其他将CNNs作为黑盒的方法，Deng等人在中提出了受传统CS和MRA方法启发的FusionNet，这促使我们将MRA等传统方法的公式作为设计所提出网络的指导。该模块受传统方法的启发，可以嵌入CNN网络中进行更好的细节提取和注入。
此外，现有的基于神经网络的增强技术没有充分挖掘和利用PAN和MS图像中的多尺度信息，在增强LRMS图像的过程中丢失了一些可能的信息。这启发我们注重信息的分层双向注入，这也是三双结构的初衷。

THE PROPOSED NETWORK

如前所述，我们的模型受到传统MRA方法的启发，其中从PAN图像提取的空间结构信息被添加到上采样LRMS图像。拟建网络的总体流程图如图3所示，包括以下部分：1)MRA嵌段（MRAB），其结构基于MRA通用公式；2)多尺度卷积特征提取模块（MSCB） 用于进一步提高融合图像的质量和增强网络的学习能力；3)三双架构，即，双层次、双分支、双向，充分利用多尺度信息。

MRAB

让我们关注物理MRA公式（2），其中要注入的空间细节，即，G⊙(P−P_L)仅从具有适当注入系数G的PAN图像中提取。因此，传统MRA方法可以等效地由以下网络体系结构表示，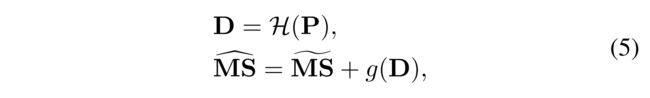
其中H（·）由潜在卷积层表示，旨在从PAN图像中提取细节D。此外，g（·）用空间注意力来表示，模拟了（2）中细节注入系数的规律。此外，上采样MS图像~ MS可以通过简单的PixelShuffle上采样操作来实现。(5）中的第一个公式可以看作PAN空间细节，即：P-PL，而（5）中的第二个公式等价于MRA公式（2），其中g（·）表示所涉及图像之间的非线性关系，而不是（2）中的线性关系。总之，MRA块（MRAB）由三部分组成：1）LRMS图像的上采样，2）特征图的提取，以及3）用于细节注入的空间注意力模块。MRAB的详细信息见图2（b）。
1) Upsampling LRMS Image：
在图2（b）中，第一步是将原始LRMS图像上采样到与GT图像相同的大小。在以往的全色锐化研究中，LRMS图像通常通过插值或反卷积操作进行尺度提升。Shi等人提出了一种有效的子像素卷积操作（称为PixelShuffle），其学习一组滤波器以将低分辨率特征升级为高分辨率输出。PixelShuffle在应用于单幅图像超分辨率问题时获得了很高的性能。因此，我们将PixelShuffle引入到我们的模型中，以提高LRMS图像的性能。特别地，通过卷积获得具有c×$r^2$通道的特征映射（其中r是LRMS和PAN图像之间的尺度放大因子），然后通过周期性的混洗产生高分辨率图像。
2) Extracting Feature Maps：
如上所述，传统的MRA方法通过计算PAN图像和低通滤波的PAN图像之间的差异来提取细节。因此，最终结果取决于所采用的预定义滤波器，所述预定义滤波器可能机械地丢弃一些期望的信息。由于使用了卷积层，可以学习并动态调整一组参数，以彻底探索特定细节并选择预期特征。此外，为了使模型适应不同的数据集，并避免固定滤波器带来的失配问题，我们通过学习（5）中的映射H（·）来提取端到端的高频信息。Zhang等人使用ResNet块作为特征提取的基本结构。然而，为了保留更多的原始图像信息和减少计算负担，我们只采用一个ResNet块来构成TDNet中的PAN分支。
如图2（b）所示，通过图3所示的PAN分支获得从PAN图像提取的细节。

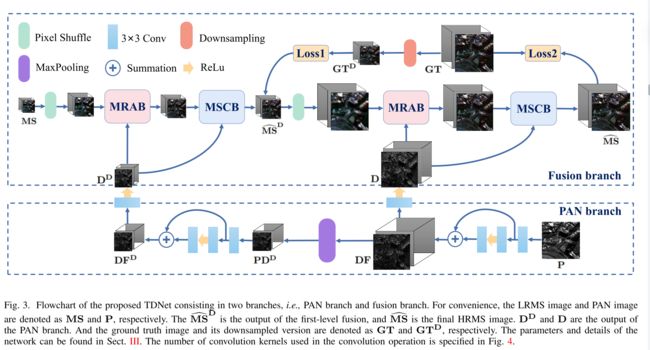
与传统MRA方法的不同之处在于MS图像被上采样两次，即，使用比例因子2（当r等于4时）。PAN分支的详细信息见图4。
3) Spatial Attention Module for Detail Injection：
回顾原始MRA公式（2）和MRA启发的公式（5），我们可以注意到（2）中的细节图像D乘以G等价于空间注意力。由于注入系数G通常取决于MS和P，因此它促使我们设计包含这两个分量的空间注意。具体来说，我们将~MS和D连接在一起进行卷积运算，如图2（b）所示，目的是学习包含MS和P图像的充分特征的权重矩阵W ∈ $R^{H\times W\times c}$。提出的注入策略是将PAN分支获得的学习特征D与权值矩阵W相乘，然后将其与PixelShuffle生成的~ MS相加，得到MRAB输出。

MSCB

虽然MRAB可以产生具有物理可解释性的竞争结果，但所获得的网络结构没有深层，限制了特征提取及其非线性拟合能力。因此，我们在我们的模型中引入了一个由Yuan等人启发的多尺度卷积块（表示为MSCB），以加深网络。图5示出了MSCB及其相应参数的细节。

Overall Structure of Triple-Double Network

为了解决LRMS和GT图像之间的不同大小的问题，传统方法直接将LRMS图像上采样到GT图像大小（通常利用因子4的上采样）。然而，这样的操作可能导致空间损失，甚至引起图像失真。通过考虑尺度差异问题，充分利用多尺度信息，设计了三重网络（TDNet），即双级、双支、双向。
整体的TDNet的架构见图3：
1) Double-branch：
从图3中可以清楚地看到，网络被分成两个分支，即，PAN分支和融合分支。PAN分支将PAN图像作为唯一输入。该算法提取并表示多尺度空间特征，并将其注入融合分支以提供足够的空间细节。融合分支的目标改为融合输入LRMS图像和来自PAN分支的多尺度空间特征以获得最终HRMS图像。融合分支包含前面提到的一些基本策略，例如MRAB和MSCB。
2) Double-level：
在这项工作中，我们使用两级策略对MS图像进行上采样，其中MS图像被上缩放到其两倍大小（即，对于每个级别，放大因子为2），从而利用多尺度特征进行全色锐化。特别地，PAN分支和融合分支都具有双层结构，以具有更好的分辨率增强能力。
3) Double-direction：
由于采用了双层结构，设计一种双向网络结构（称为双向） 是充分利用PAN和MS图像多尺度信息的一种有前途的策略。如图3中TDNet的流程图所示，PAN分支和融合分支都是双层结构。前者将PAN图像降采样到较小的尺寸，而后者将LRMS图像升采样到较大的尺寸。两个分支的信息流方向相反，相互对应，从而实现分支之间的信息融合。类似的策略已在之前的基准测试工作中被证明是有效的。
综上所述，通过上述三个方面，提出了TDNet的最终体系结构，即：双支、双级、双向。特别地，双分支以已知的LRMS图像和PAN图像作为输入，实现了有区别的特征表示。双层结构使网络能够利用多尺度特性，双向结构加强了两个分支之间的相互作用，提高了网络性能。

Loss Fuction

如前所述，我们的TDNet架构包含一个双层结构，这导致两个损失函数。设~MS^D ∈ $R^{2h\times 2w}$和~MS ∈ $R^{H\times W}$分别代表第一级和第二级的输出，并且令GT^D ∈ $R^{2h\times 2w}$和GT ∈ $R^{H\times W}$分别表示第一级和第二级的GT图像。我们为两个级别的监督学习定义以下损失函数，

其中γ ∈ [0，1]在训练阶段是常数，γ的大小在第IV节中深入讨论。具体地，Loss_l和Loss₂定义如下，