FCN+:全局感知的卷积
全卷积网络是语义分割的开创性工作,然而,FCN的感受野有限,不能有效捕捉语义分割所需要的全局上下文信息,因此FCN被后来的方法打败,比如增加不同size的滤波器来获得多尺度感受野,然而这势必增加参数数量。不同于空洞卷积(扩大感受野,并且不引入额外参数),作者提出全局感受野卷积(GRC,global receptive convolution),GRC直接提供了全局感受野,并且不引入额外参数。通过内置GRC, FCN可以实现与最先进的语义分割任务方法相当的性能,这在PASCAL VOC 2012,cityscape和ADE20K上得到了验证。
来自:FCN+: Global Receptive Convolution Makes FCN Great Again
一个卷积层包含多个filter,每个filter的kernel数量等于输入张量的通道数,输出张量的通道数量就是filter的个数,一个filter中的各个kernel是不同的;
可以理解为不同的filter提取不同的局部特征,filter内的kernel不同是为了获取输入张量上不同通道的局部信息,最后加和得到该filter对应的局部特征相似度;
目录
- 背景概述
- 方法
-
- 预备知识
- GRC
- 结果
背景概述
语义分割是密集预测任务,目的是为每个像素分配一个类别。挑战包括:
- 挑战一:同一个对象,超大尺度的和超小尺度的容易被忽略。为了缓解这个问题,多尺度特征表示被用于编码不同尺度的对象。
- 挑战二:不同对象,相似的视觉外观导致边界混淆,为了分割边界,有必要将全局上下文信息集成到每个像素的表示中,以便利用整体场景理解边界。
FCN具有鲁棒性,然而其感受野有限,不能得到全局上下文信息。PSPNet采用多个尺度的pooling来引入多尺度上下文,但pooling本身会丢失空间细节信息。Deeplab使用多个膨胀率的空洞卷积进行采样,但空洞卷积容易丢失邻居像素的信息。可变形卷积学习采样位置会增加参数并且学习的位置偏移通常不准确。ViT捕捉全局信息效果虽好,但对资源的开销更大。
经典卷积的方法假设滤波器的不同通道共享相同的采样位置,通常,这些位置被限制在固定的3×3网格中,在极端情况下,1×1卷积不管是否膨胀,或者可变形,无论涉及多少通道,它们也只在一个空间点上采样。为了打破僵局,作者提出GRC,动机是滤波器的不同通道可以有不同的采样位置,从而扩大感受野,并且不引入额外参数。
在图1中,GRC用于1×1卷积进行说明,GRC首先将滤波器的通道分为两组。然后根据通道索引将第一组的网格采样位置移动到不同的坐标(覆盖整个输入张量),使滤波器能够捕获全局上下文信息。第二组在当前位置采样,抽象原有位置上的信息。
因此,GRC可以将全局上下文整合到每个像素的原始位置信息中。这可以有效地解决挑战二,获得更好的密集预测结果。GRC简单而有效,可灵活应用于任何滤波器。
- 图1:GRC与其他卷积的比较。a. 3×3空洞卷积,膨胀率=2。b. 3×3可变形卷积,变形卷积学习每个空间位置的偏移量,以扩大感受野。对于a和b,其滤波器的不同通道共享完全相同的网格采样位置。c. 1×1全局感受野卷积,GRC沿着通道维度将1×1 kernel分为两组:浅蓝色的立方体和其他颜色的立方体。浅蓝色的一组对中心像素进行卷积,保持原始位置信息。而其他颜色组则被转移到其他空间位置,以捕获全局上下文信息。请注意,1×1 GRC具有全局感受野。
- 最后,信息被汇集得到该滤波器的输出值,即作为该滤波器在浅蓝色采样位置输出的激活值。
然后,作者将GRC应用于FCN的特征提取器,用GRC替换标准卷积,称之为FCN+。在这里,选择FCN有两个原因:
- FCN是语义分割中最流行的方法之一,它被用作许多SOTA方法的baseline。这些方法使用基于FCN的架构,使用基于GRC的编码器,FCN+可以高效与复杂的方法竞争。
- FCN本身包含多尺度表示,可以缓解挑战一,得益于GRC和FCN, FCN+不仅可以提供多尺度表示,还可以结合全局上下文信息,同时解决两个语义分割挑战。
方法
预备知识
输入卷积的3D特征为 F ∈ R H × W × C F\in R^{H\times W\times C} F∈RH×W×C,卷积的所有滤波器为 W ∈ R C × K × K × C ′ W\in R^{C\times K\times K\times C'} W∈RC×K×K×C′, K K K为滤波器中kernel的size, C C C为每个滤波器中kernel的数量, C ′ C' C′为滤波器数量。为了简单,我们考虑仅包含单个滤波器的卷积,即 C ′ = 1 C'=1 C′=1。则输出为: F ′ ( h 0 , w 0 ) = ∑ c = 0 C − 1 ∑ ( h , w ) ∈ N W ( c , h , w ) ∗ F ( h 0 + h , w 0 + w , c ) F'(h_{0},w_{0})=\sum_{c=0}^{C-1}\sum_{(h,w)\in N}W(c,h,w)*F(h_{0}+h,w_{0}+w,c) F′(h0,w0)=c=0∑C−1(h,w)∈N∑W(c,h,w)∗F(h0+h,w0+w,c)其中, F ′ ( h 0 , w 0 ) F'(h_{0},w_{0}) F′(h0,w0)是输出特征位于 ( h 0 , w 0 ) (h_{0},w_{0}) (h0,w0)的值。 ∗ * ∗操作代表卷积, h , w h,w h,w为采样位置的坐标,它们都被限制在以 ( h 0 , w 0 ) (h_{0},w_{0}) (h0,w0)为中心的局部邻居区域 N N N内。 ( h 0 , w 0 ) (h_{0},w_{0}) (h0,w0)的位置称为中心采样位置, ( h 0 , w 0 ) (h_{0},w_{0}) (h0,w0)的像素称为中心像素。
对于标准的卷积, ( h , w ) (h,w) (h,w)枚举 N N N中所有的位置: N = { ( − r , − r ) , ( − r , − r + 1 ) , . . , ( r − 1 , r ) , ( r , r ) } N=\left\{(-r,-r),(-r,-r+1),..,(r-1,r),(r,r)\right\} N={(−r,−r),(−r,−r+1),..,(r−1,r),(r,r)}其中, r = [ K 2 ] r=[\frac{K}{2}] r=[2K]取决于kernel size,而kernel size决定了感受野。对于空洞卷积, ( h , w ) (h,w) (h,w)为: N = { ( − r , − r ) , ( − r , − r + d ) , . . , ( r − d , r ) , ( r , r ) } N=\left\{(-r,-r),(-r,-r+d),..,(r-d,r),(r,r)\right\} N={(−r,−r),(−r,−r+d),..,(r−d,r),(r,r)}其中, r = [ d ( K − 1 ) + 1 2 ] r=[\frac{d(K-1)+1}{2}] r=[2d(K−1)+1], d d d为膨胀率。
GRC
作者提出一种新卷积GRC。首先,将 W W W分为两组( C ′ = 1 C'=1 C′=1,准确来说,是每个滤波器分两组),默认每个组有相同的通道数,比如 C / 2 C/2 C/2。相同通道数是基于原始位置信息和全局上下文信息同等重要的假设。对于组 { 0 , . . . , C 2 − 1 } \left\{0,...,\frac{C}{2}-1\right\} {0,...,2C−1},我们像预备知识中的标准卷积一样提取信息。对于组 { C 2 , . . . , C − 1 } \left\{\frac{C}{2},...,C-1\right\} {2C,...,C−1},我们设计全局感受野采样,即 N ^ \widehat{N} N ,GRC的滤波器计算为: F ′ ( h 0 , w 0 ) = ∑ c = 0 C 2 − 1 ∑ ( h , w ) ∈ N W ( c , h , w ) ∗ F ( h 0 + h , w 0 + w , c ) + ∑ c = C 2 C − 1 ∑ ( h ^ , w ^ ) ∈ N ^ ∑ ( h , w ) ∈ N W ( c , h , w ) ∗ F ( h 0 + h ^ + h , w 0 + w ^ + w , c ) F'(h_{0},w_{0})=\sum_{c=0}^{\frac{C}{2}-1}\sum_{(h,w)\in N}W(c,h,w)*F(h_{0}+h,w_{0}+w,c)+\\\sum_{c=\frac{C}{2}}^{C-1}\sum_{(\widehat{h},\widehat{w})\in \widehat{N}}\sum_{(h,w)\in N}W(c,h,w)*F(h_{0}+\widehat{h}+h,w_{0}+\widehat{w}+w,c) F′(h0,w0)=c=0∑2C−1(h,w)∈N∑W(c,h,w)∗F(h0+h,w0+w,c)+c=2C∑C−1(h ,w )∈N ∑(h,w)∈N∑W(c,h,w)∗F(h0+h +h,w0+w +w,c)其中, N N N与预备知识中的定义一样,第一项保留了像素级表示的原始位置信息,即为 ( h 0 , w 0 ) (h_{0},w_{0}) (h0,w0)处中心像素点的特征表示。 N ^ \widehat{N} N 控制GRC的中心采样位置。 N ^ \widehat{N} N 中的偏置 ( h ^ , w ^ ) (\widehat{h},\widehat{w}) (h ,w )按照通道索引 c c c,将采样中心位置从 ( h 0 , w 0 ) (h_{0},w_{0}) (h0,w0)移动到其他位置。
通过这种方式,偏移可以涉及不同的网格采样位置,以捕获全局上下文信息。最后,通过将这两个项相加,将全局上下文信息集成到像素级表示中,如图2所示。
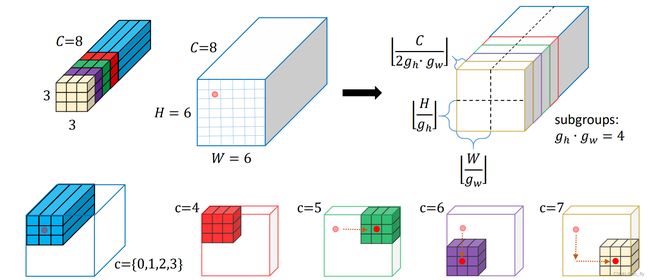
- 图2:3×3的GRC示例。这个例子展示了仅包含1个滤波器,kernel size为3×3的GRC如何卷积6×6×8输入特征图(中心像素 ( h 0 , w 0 ) = ( 1 , 1 ) (h_{0},w_{0})=(1,1) (h0,w0)=(1,1),如浅红点所示)。
( h ^ , w ^ ) (\widehat{h},\widehat{w}) (h ,w )的计算如下。我们进一步将 { C 2 , . . . , C − 1 } \left\{\frac{C}{2},...,C-1\right\} {2C,...,C−1}分组,每个子集合包含 [ C 2 g h ⋅ g w ] [\frac{C}{2g_{h}\cdot g_{w}}] [2gh⋅gwC]个通道。对应着,我们沿着2D空间方向将输入特征划分为 g h ⋅ g w g_{h}\cdot g_{w} gh⋅gw个patch。每个patch的像素数为 [ H g h ] ⋅ [ W g w ] [\frac{H}{g_{h}}]\cdot[\frac{W}{g_{w}}] [ghH]⋅[gwW],因此偏移为: h ^ = i ⋅ [ H g h ] , w ^ = j ⋅ [ W g w ] \widehat{h}=i\cdot [\frac{H}{g_{h}}],\widehat{w}=j\cdot [\frac{W}{g_{w}}] h =i⋅[ghH],w =j⋅[gwW]其中, i , j i,j i,j为patch的index, i ∈ [ 0 , g h − 1 ] , j ∈ [ 0 , g w − 1 ] i\in[0,g_{h}-1],j\in[0,g_{w}-1] i∈[0,gh−1],j∈[0,gw−1]。
因此, N ^ \widehat{N} N 为所有可能的 i , j i,j i,j组合: N ^ = { ( 0 , 0 ) , ( 0 , [ W g w ] ) , . . . , ( ( g h − 2 ) ⋅ [ H g h ] , ( g w − 1 ) ⋅ [ W g w ] ) , ( ( g h − 1 ) ⋅ [ H g h ] , ( g w − 1 ) ⋅ [ W g w ] ) } \widehat{N}=\left\{(0,0),(0,[\frac{W}{g_{w}}]),...,((g_{h}-2)\cdot[\frac{H}{g_{h}}],(g_{w}-1)\cdot[\frac{W}{g_{w}}]),((g_{h}-1)\cdot[\frac{H}{g_{h}}],(g_{w}-1)\cdot[\frac{W}{g_{w}}])\right\} N ={(0,0),(0,[gwW]),...,((gh−2)⋅[ghH],(gw−1)⋅[gwW]),((gh−1)⋅[ghH],(gw−1)⋅[gwW])}其中, N ^ \widehat{N} N 共包含 g h ⋅ g w g_{h}\cdot g_{w} gh⋅gw个偏移坐标。它几乎涵盖了整个输入特征图。
结果
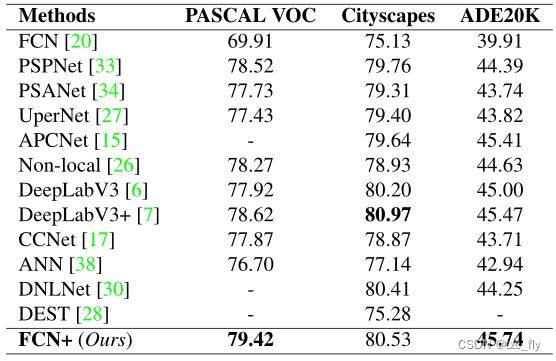
下面比较基于PASCAL VOC 2012,cityscape和ADE20K的最先进方法的分割结果。所有的结果都是基于MMSegmentation得到的: