376.摆动序列【贪心算法】

376. 摆动序列

题⽬链接：https://leetcode-cn.com/problems/wiggle-subsequence/

如果连续数字之间的差严格地在正数和负数之间交替，则数字序列称为摆动序列。第⼀个差（如果存在的话）可能是正数或负数。少于两个元素的序列也是摆动序列。

例如， [1,7,4,9,2,5] 是⼀个摆动序列，因为差值 (6,-3,5,-7,3) 是正负交替出现的。

相反, [1,4,7,2,5] 和 [1,7,4,5,5] 不是摆动序列，第⼀个序列是因为它的前两个差值都是正数，第⼆个序列是因 为它的最后⼀个差值为零。

给定⼀个整数序列，返回作为摆动序列的最⻓⼦序列的⻓度。 通过从原始序列中删除⼀些（也可以不删除）元素来获得⼦序列，剩下的元素保持其原始顺序。

示例 1:

输⼊: [1,7,4,9,2,5]

输出: 6

解释: 整个序列均为摆动序列。

示例 2:

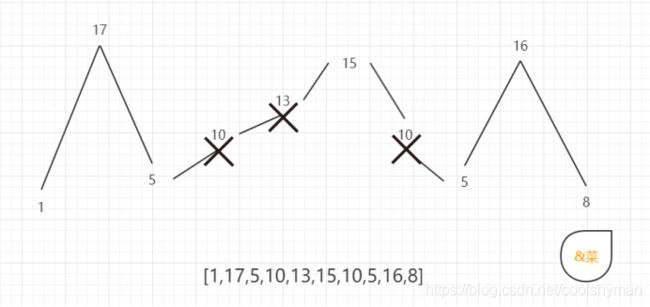
输⼊: [1,17,5,10,13,15,10,5,16,8]

输出: 7

解释: 这个序列包含⼏个⻓度为 7 摆动序列，其中⼀个可为[1,17,10,13,10,16,8]。

示例 3:

输⼊: [1,2,3,4,5,6,7,8,9]

输出：2

本题思路：

子序列可以通过从原始序列中删除一些（也可以不删除）元素来获得，剩下的元素保持其原始顺序。咋一看感觉这题目劝退了，这要求达到最大摆动序列需要删除哪些元素？

首先用较为复杂的示例2做分析，如图所示：

局部最优：删除单坡度上的节点（不包括单坡度两端的节点），那么这个坡度就可以有两个局部峰值。

整体最优：整个序列有最多的局部峰值，从⽽达到最⻓摆动序列。

局部最优推出全局最优，并举不出反例，那么可以试一试贪⼼算法！

（以下说明的峰值都是指局部峰值）

实际操作上，其实连删除的操作都不⽤做，因为题⽬要求的是最⻓摆动⼦序列的⻓度，所以只需要统计数组的峰值数量就可以了（相当于是删除单⼀坡度上的节点，然后统计⻓度）

这便是贪⼼所贪的地⽅，让峰值尽可能的保持峰值，然后删除单⼀坡度上的节点。

本题代码实现中，还有⼀些技巧，例如统计峰值的时候，数组最左⾯和最右⾯是最不好统计的。

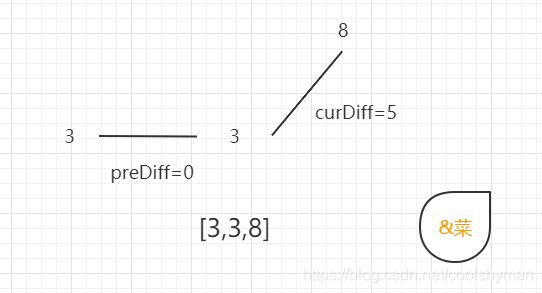
例如序列[3,8]，它的峰值数量是2，如果靠统计差值来计算峰值个数就需要考虑数组最左⾯和最右⾯的特殊情况。

所以可以针对序列[3,8]，可以假设为[3,3,8]，这样它就有坡度了即preDiff = 0，如图：

针对以上情形，count初始为1（默认最右⾯有⼀个峰值），此时curDiff > 0 && preDiff <= 0，那么count++（计算了左⾯的峰值），最后得到的count就是2（峰值个数为2即摆动序列⻓度为2）

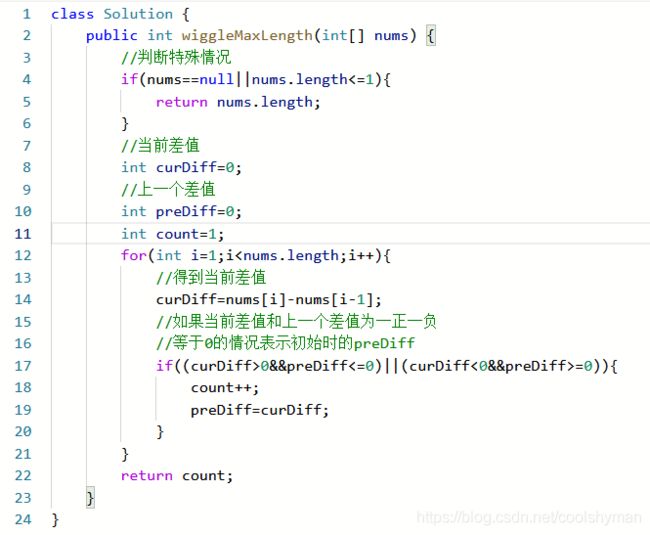
java代码整体如下：

 

时间复杂度O(n)、空间复杂度O(1)

什么是贪心算法？

贪心的本质是选择每一个阶段的局部最优，从而达到全局最优。

举个例子：

假如钱包里有一堆钞票，你可以拿走5张，如果想要尽可能的拿到最大的金额，你要如何拿？

每次拿最大的，最终结果就是拿走最大的金额数。

每次拿最大的就是局部最优，最后拿走最大数额的钱就是推出全局最优。