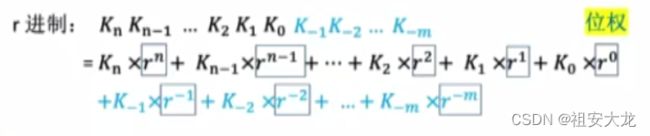计算机组成原理知识点总结——第二章数据的表示和运算
目录
- 一、数制与编码
-
- ⭐r进制计数法⭐
- BCD码（大纲已删除）
- 二、定点数的表示与运算
-
- 无符号整数的表示和运算
- ⭐带符号整数的表示和运算（原反补）⭐
- 定点小数
- 奇偶校验（大纲已删除）
- 定点数的运算
- C语言中的强制类型转换
- 数据的存储和排列
- 三、浮点数的表示与运算
-
- ⭐浮点数的表示⭐
- ⭐IEEE754标准⭐
- 浮点数的运算
- 四、算术逻辑单元
-
- 电路的基本原理
- ⭐算数逻辑单元的功能和结构⭐
一、数制与编码
⭐r进制计数法⭐
基数：每个数码位所用到的不同符号的个数，r进制的基数为r
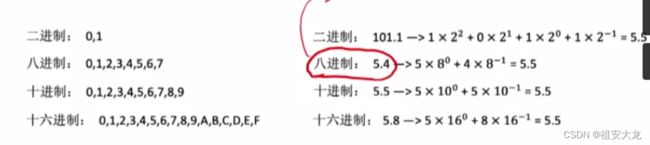
各种进制常见的书写方式
十进制转其他进制（小数部分）
真值和机器数
真值：符合人类习惯的数字
机器数：数字实际存到机器里面的形式，正负号需要被“数字化”
BCD码（大纲已删除）
用4个二进制对应一个十进制
⭐8421码⭐
四个二进制的权重分别为8421，相互映射关系如下
如果两个8421码相加得到的值不再映射表内，则加上8421码的6，得到的结果就是我们的8421码的结果。
余3码：8421码+(0011)2
2421码：改变权值定义，四位的权值为2421
二、定点数的表示与运算
无符号整数的表示和运算
计算机硬件能支持的无符号整数位数有上限
当数值超过位数上限，只能保存低位数值。
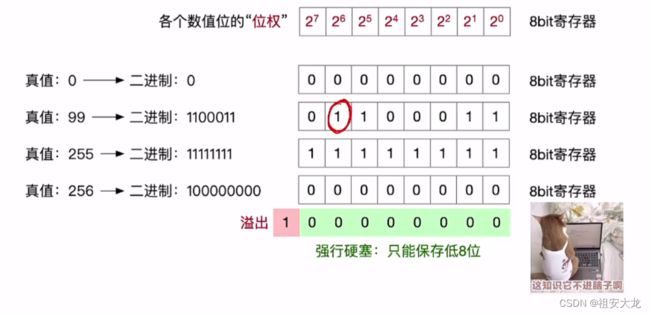
无符号整数
- 全部二进制位都是数值位，没有符号位，第i位的位权是2i-1
- n bit无符号整数表示范围0~2n-1，超出则溢出，意味着该计算机无法一次处理这么多
- 可以表示的最小的数，全0，可以表示最大的数，全1
无符号整数的加法
从最低位开始，按位相加，并往更高位进位
⭐无符号整数的减法⭐
- “被减数”不变，“减数”全部位按位取反，末位+1，减法变加法，（取补码相加）
- 从最低位开始，按位相加，并往更高位进位。
⭐加减法得出的结果溢出部分丢弃。⭐
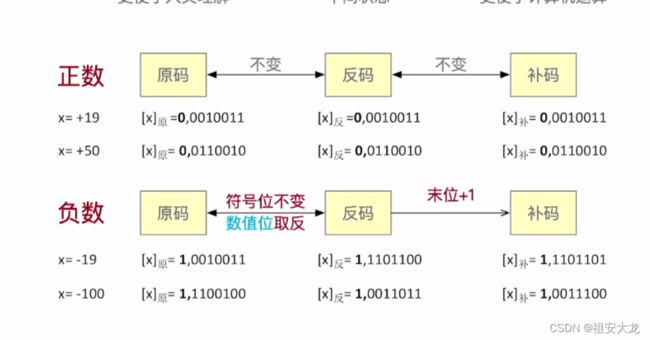
⭐带符号整数的表示和运算（原反补）⭐
原码
- 最高位为符号位，0为正，1为负，其余位为数值位。
- 若机器字长n+1位，带符号整数的源码表示范围：-(2n-1)<=x<=2n-1
- 真值0有两种形式，+0和-0，[+0]原=00000000，[-0]原=10000000
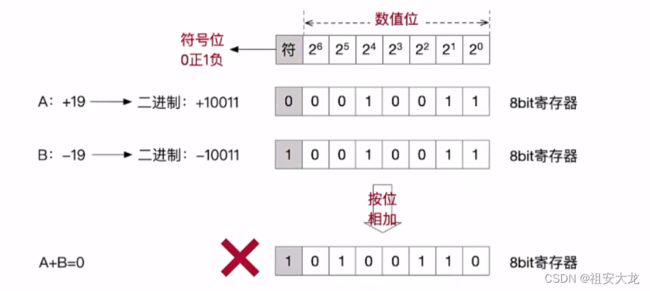
缺点：符号位不能参与运算，需要设计复杂的硬件电路才能处理，费用大。
⭐原码——>反码——>补码的转换⭐
⭐补码——>原码⭐
从右往左找到第一个1，这个1左边的所有“数值位”按位取反。
补码
补码数值不能解读位“位权”
⭐补码的加法⭐
从最低位开始，按位相加（符号位参与运算），并往更高位进位。得到的结果转为原码，就能得到最终的结果。
⭐⭐补码的减法⭐⭐
减数全部位按位取反，末位+1
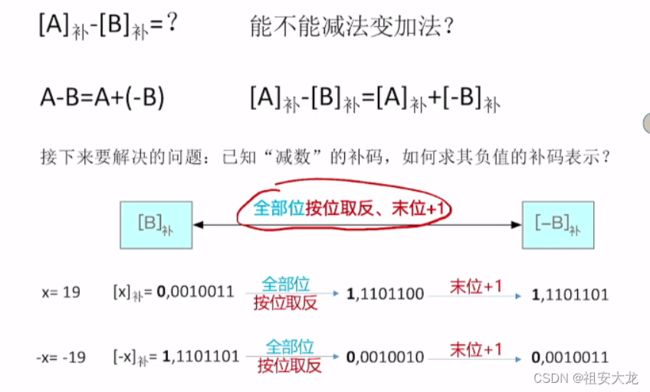
小节总结
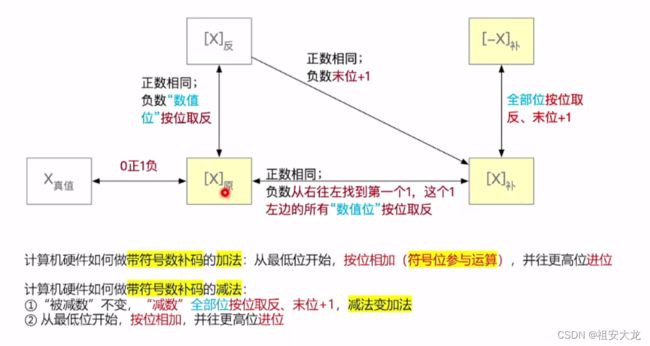
原反补的特性对比
- 原码和反码的合法表示范围完全相同，都有两种方法表示真值0
- 补码的合法表示范围比原码多一个负数，只有一种方法表示真值0
⭐常见考点⭐
- 两个数A和B进行某种运算后，是否发生溢出？——手算做题可以带入十进制验证，是否超出合法范围。
移码
- 补码的基础上将符号位取反。注：移码只能用于表示整数
- 若机器字长n+1位，移码整数的表示范围：-2n<=x<=2n-1（与补码相同）
- 移码的合法表示范围比原码多一个附属，只有一种方法表示真值0
定点小数
定点整数默认小数点位置在最低位后，定点小数默认小数点位置在符号位后，即次高位。
定点小数的编码表示：原码、反码、补码
原码
符号位“0/1”，对应“正/负”
⭐定点小数的原码反码补码转换和定点整数的一模一样⭐
定点小数的加/减运算（与定点整数一样）
位数扩展时，定点小数在尾部进行扩展，定点整数在符号位和原数值位之间扩展。
奇偶校验（大纲已删除）
定点数的运算
1、定点数的移位运算
移位：通过改变各个数码位和小数点的相对位置，从而改变各数码位的位权。可用移位运算实现乘法、除法。但是由于原码、反码、补码的位数有限，并不能每次都很精确的实现乘除法的操作。
⭐原码的算数移位⭐
符号位保持不变，仅对数值位进行移位。
算数右移：高位补0，低位舍弃。若舍弃的位=0，相当于÷2；若舍弃的位!=0，则会丢失精度。
算数左移：低位补0高位舍弃。若舍弃的位=0，则相当于x2；若舍弃的位!=0，则会出现严重误差。
⭐反码的算数移位⭐
正数和原码一样，负数补的数为1
⭐补码的算数移位⭐
正数和原码一样
负数补码中，最右边的1及其右边同原码，最右边的1的左边同反码。规则如下：
右移（同反码）：高位补1，低位舍弃
左移（同原码）：低位补0，高位舍弃
逻辑移位
左移右移后，补0即可
针对无符号数的移位。
循环移位
左移右移后，移出的位补充至需要补充的位置。
带进位的循环移位
其实就是添加了一位进行循环移位。
2、定点数的乘法的运算
原码一位乘法
- 符号单独处理，两个数的符号位进行异或处理得到新值的符号位
- 数值位取绝对值进行乘法计算。
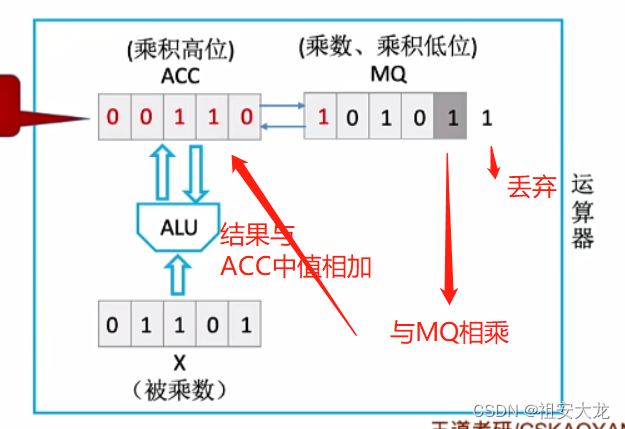
实现方法：先加法再位移，重复n次。
乘数存储到MQ中，被乘数存储到X中，ACC寄存器清零。
乘数最低位乘被乘数，然后与ACC值相加，然后ACC和MQ进行逻辑右移一位，将MQ中最低位丢弃（不会再使用），然后重复最低位与被乘数相乘后，与ACC寄存器中的数相加。执行n轮。
补码的一位乘法（Booth算法）
- 进行n轮加法、移位，最后再多来一次加法
- 每次加法根据当前MQ中的最低位、辅助位来确定加什么值。
- 每次移位时**“补码的算数右移”**
- 乘数的符号位参与运算。
加法规则
- 辅助位-MQ中“最低位”=1时，（ACC）+ [X]补
- 辅助位-MQ中“最低位”=0时，（ACC）+ 0
- 辅助位-MQ中“最低位”=-1时，（ACC）+ [-X]补
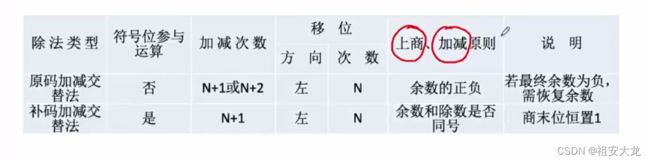
3、定点数的除法运算
原码除法：恢复余数法
先商1，ACC和X中的值做差，更新到ACC，如果得到负数则代表原ACC中的数比较小，除法出错，则ACC+X中值恢复上一次ACC中的值，然后商0，存储再MQ的最后一位，然后逻辑左移。重复n次得出结果。最终将两个数的符号位异或，得到最高位。
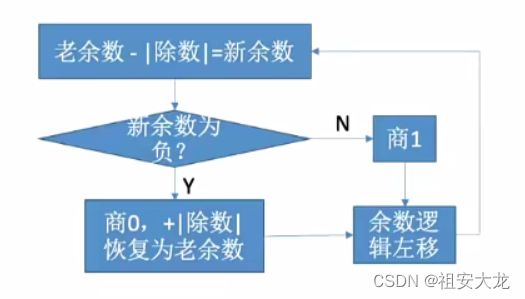
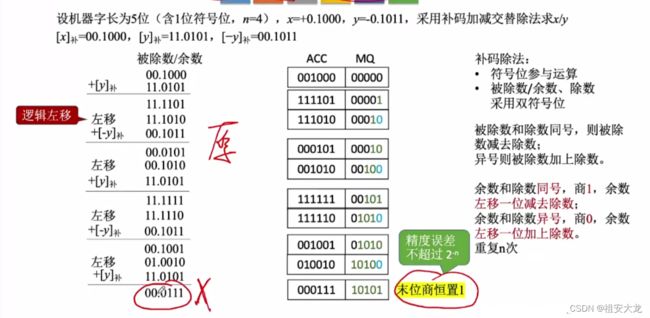
原码除法：加减交替法
- 若余数为负，则可直接商0，让余数左移1位再加上|除数|，得到下一个新余数
- 若余数为正，则商1，让余数左移1为再减去|除数|，得到下一个新的余数。
- 最后时，若余数为负，需商0，并+[|除数|]补得到正确的余数。
- 最后的符号位也是两个数的符号位进行异或得出。
补码除法：加减交替法
- 符号位参与运算
- 被除数/余数、除数采用双符号位
除法运算总结
C语言中的强制类型转换
C语言中的定点整数都是用“补码”存储。
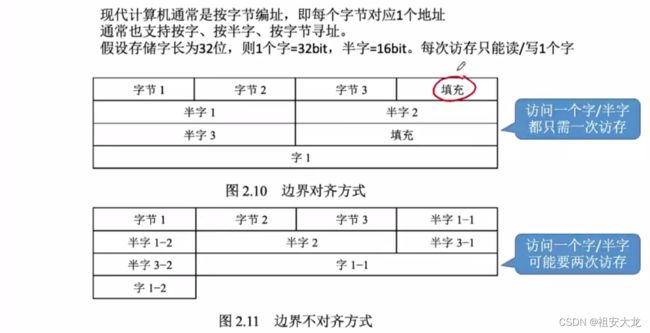
数据的存储和排列
1、大小端模式
多字节数据在内存例一定是占连续的几个字节。
大端方式（便于人类阅读）
- 按地址由低到高，有效字节从高到低存储。
小端方式（便于机器处理）
- 按地址由低到高，有效字节从低到高存储。
值 01 23 45 67 H
2、边界对齐
三、浮点数的表示与运算
⭐浮点数的表示⭐
定点数可表述的数字范围有限，但我们不能无限制地增加数据的长度。
浮点数可以表示为⭐N=rExM⭐
E称为阶码，M称为尾数，r为阶码的底，通常为2。
⭐阶码E反映浮点数的表示范围及小数点的实际位置；尾数M的数值部分的位数n反映浮点数的精度。⭐
浮点数尾数的规格化
⭐规格化浮点数⭐：规定尾数的最高数值位必须是一个有效值。
左规：当浮点数运算的结果为非规格化时要进行规格化处理，将尾数算数左移一位，阶码减1.
右规：当浮点数运算的结果尾数出现溢出（双符号位为01或10）时，将尾数算数右移一位，阶码加1.
特点
表示范围已经在大纲中删除了，了解即可。
⭐IEEE754标准⭐
⭐阶码用移码表示⭐
移码=真值+偏置值（2n-1），⭐但在IEEE754标准中偏置值取2n-1-1⭐
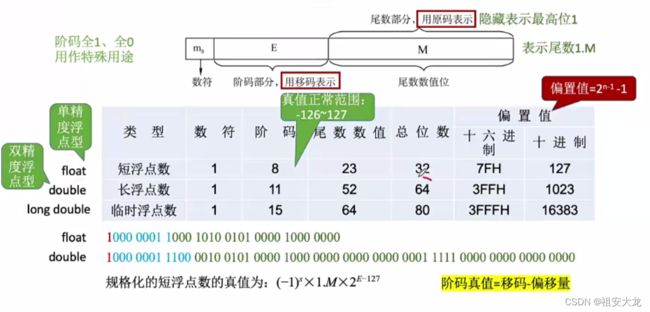
例题
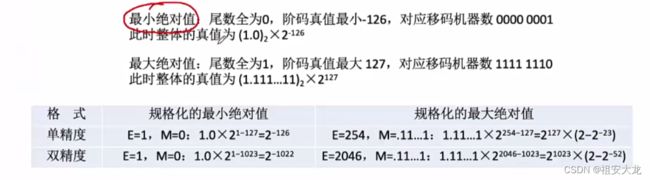
阶码全1、全0用作特殊用途
- ⭐只有1<=E<=254时，真值=(-1)Sx1.Mx2E-127⭐
- 当阶码E全为0，尾数M不全为0时，表示非规格化小数 ±(0.xxxx……x)2x2-126
- 当阶码E全为0，尾数M全为0时，表示真值 ±0
- 当阶码E全为1，尾数M全为0时，表示无穷大±∞
- 当阶码E全为1，尾数M不全为0时，表示非数值“NaN"(Not a Number)，如0/0、∞-∞的非法运算。、
浮点数的运算
浮点数加减运算步骤
- 对阶
将两个数的小数点位置对其，即使两个数的阶码相同，阶数小的向阶数大的看齐。 - 尾数加减
将对阶后的尾数按定点数加减运算 - 规格化
对得到的结果进行规格化 - 舍入
超出尾数有效位的则进行舍入 - 判溢出
阶码溢出则导致溢出，进行溢出判断。
浮点数的强制类型转换
⭐int转float转换只会损失精度，不会发生溢出。⭐
⭐float向int转换可能损失精度和溢出。⭐
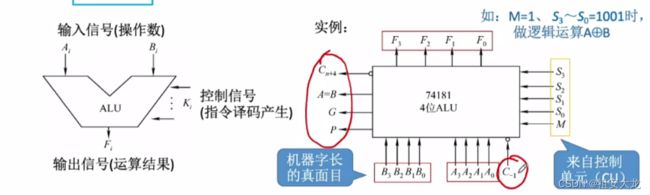
四、算术逻辑单元
基本结构：输入、输出、⭐控制（CU）⭐
实现算数运算、逻辑运算、辅助功能（位移、求补等）
电路的基本原理
基本的逻辑运算
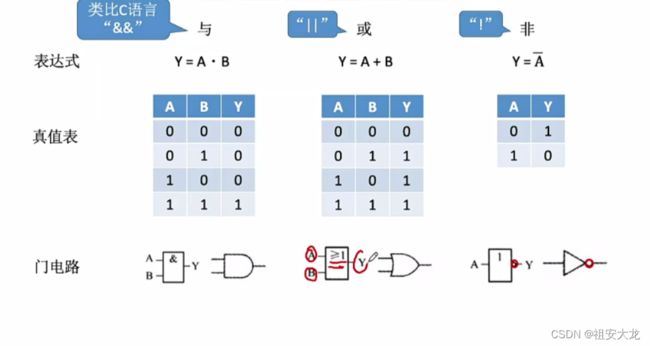
优先级：与>或
A(C+D)=AC+AD——分配律
ABC=A(BC)——结合律
A+B+C=A+(B+C)——结合律
本质上逻辑表达式是对电路的数学化描述，简化逻辑表达式，就是在简化电路。
复合逻辑
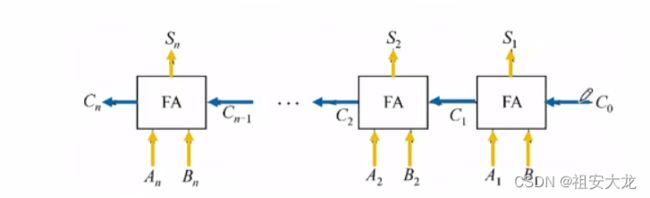
一位全加器FA
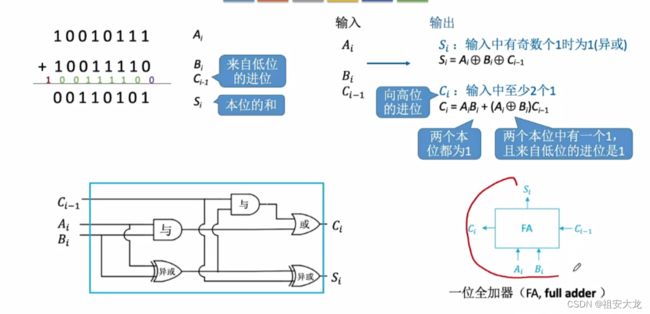
和表达式：Si=Ai⊕Bi⊕Ci-1
进位表达式：Ci=AiBi+(AI⊕Bi)C~i-1
串行加法器
- 增加一位进位触发器，只有一个全加器，数据逐位串行送入加法器中进行运算。进位触发器用来寄存进位信号，以便参与下一次运算。
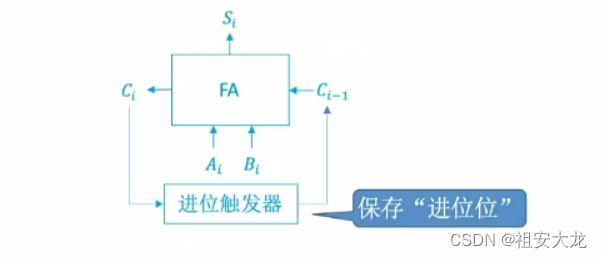如果操作数长n位，加法就要分n次进行，每次产生一位和，并且串行逐位地送回寄存器。
并行加法器（不是重点）
- 串行进位的并行加法器：把n个全加器串接起来，就可进行两个n位数的相加。
- 串行进位又称为行波进位，每一级进位直接依赖于前一级的进位，即进位信号时逐级形成的。
速度很大程度上一列全加器中进位产生的速度。
⭐算数逻辑单元的功能和结构⭐
1、补码加减运算器
加法器原理
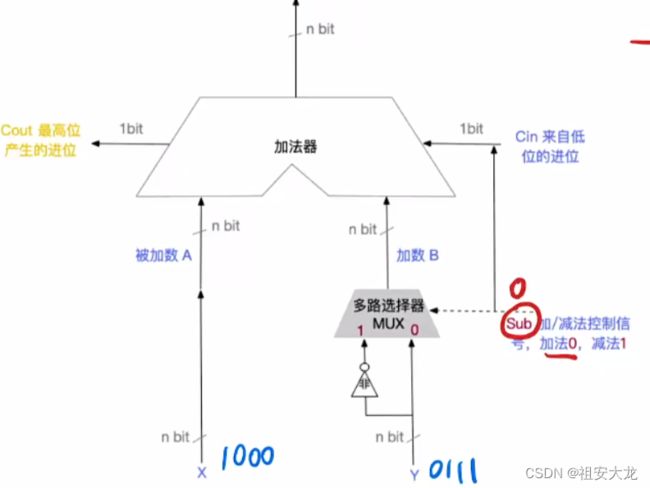
由Sub控制多路选择器，Sub等于0则为加法，多路选择器选择为0的路径，输入Y不变，直接参与加法运算。Sub等于1时，代表减法，多路选择器选择为1的路劲，输入Y经过非门，全部取反，末尾+1，减法变加法。
无符号整数的加法/减法也可用该电路实现，但是判断溢出的方式不同，设计标志位的知识。
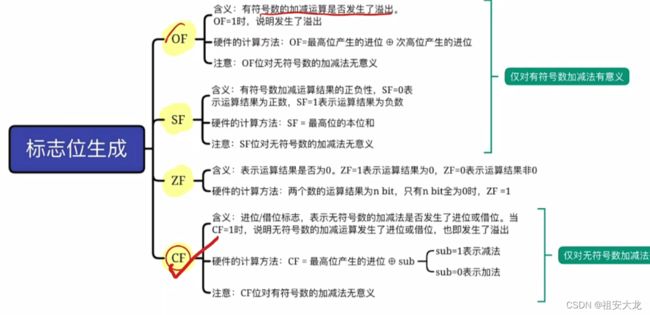
2、标志位的生成
OF溢出标志，溢出时为1，否则置0
- ⭐有符号数⭐的加减运算是否产生溢出
- ⭐OF=最高位产生进位⊕次高位产生的进位⭐
SF符号标志，结果为负时置1，否则置0
⭐有符号数⭐加减运算结果的正负性
ZF零标志，运算结果为0时为1，否则为0
- 仅对无符号数有意义
CF进位/借位标志，进位/借位时置1，否则置0。
- 仅对无符号数有意义
- 当CF=1时说明无符号数的加减运算发生了进位或借位，也即发生了溢出。
- CF=最高位产生的进位⊕Sub（Sub=1表示减法，Sub=0表示加法）
