【数据结构-算法题】C++| 二叉树全家桶 | 二叉树的遍历 |前序遍历 中序遍历 后续遍历 层序遍历 |学习笔记
文章目录
- 前言
- 一、前序遍历
-
- 1.1.一些基础知识
- 1.2.前序遍历的递归法
- 1.3前序遍历的迭代法
- 二.中序遍历
-
- 2.1中序遍历的递归法
- 2.2中序遍历的迭代法
- 三.后序遍历
-
- 3.1后序遍历的递归法
- 3.2后序遍历的迭代法
- 四.层序遍历
- 没写完的地方
前言
本节内容均出自力扣上的二叉树专项题,这里且当做自己一个总结篇了。
写这个总结篇的原因,源自于之前刷了题一直忘,后面才反应过来刷力扣题也需要自己总结一下,不然依然不是自己的东西,这样总结一下会好很多。
部分求解方式参考了力扣的官方解题过程,代码随想录大佬的求解过程:代码随想录
强烈推荐大家看他的课
一、前序遍历
1.1.一些基础知识
之前在做题的时候,我经常把一些基础的概念给弄混,比如我觉得深度优先搜索就是递归。但是概念上没有这么简单,是有讲究的。
1)二叉树的深度优先搜索:包括前序遍历,中序遍历,后序遍历。经常用的递归方法就是这种深度优先搜索思想的体现,当然我们也可以使用栈来实现迭代法。
2)二叉树的广度优先搜索:经常用的只有一个层序遍历。通常会使用队列进行算法实现。
1.2.前序遍历的递归法
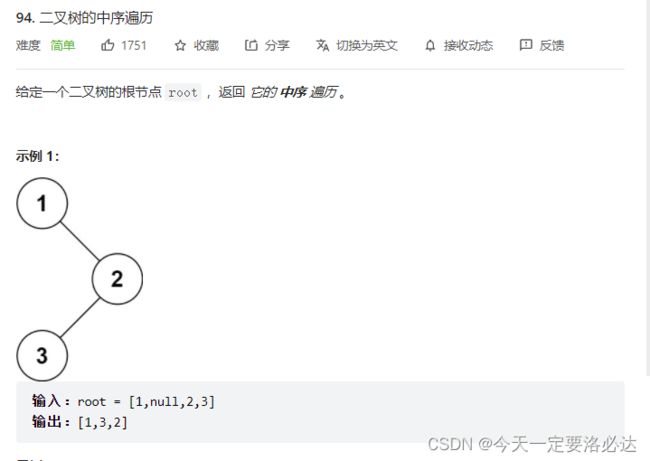
看看题目:

再看看题目给的基础代码:输入一个根结点,就要返回一个vector数组。看到这里,我大概就明白了在solution里应该还要自定义一段函数进行递归,而不能用它给的preorderTraversal进行递归。这是因为如果用preorderTraversal进行递归的话,那么系统会反复的输出vector数组,那肯定是要报错的。最后的要求仅仅是返回一个vector数组就行。在后面的中序遍历,后序遍历也是这个道理。
首先给出递归法:这里定义了一个用以反复递归的新函数:qian。这个新的递归函数不会反复输出最后的res结果。preorderTraversal仅仅成为了一个入口函数。
class Solution {
public:
void qian(vector<int>& res,TreeNode* root){
if(!root){
return;
}
res.push_back(root->val);
qian(res,root->left);
qian(res,root->right);
}
vector<int> preorderTraversal(TreeNode* root) {
vector<int>res;
qian(res,root);
return res;
}
};
那么递归的停止条件是什么呢:?

递归终止的调剂是访问到的结点为空了,也就是我在访问一个根本就不存在的结点的时候,此时递归就返回。在很多二叉树的题目中,返回的判断语句都是这样:(可能return那里会有一定区别,比如求深度的题是return 0)
if(!root){
return;
}
写成另外一种格式也是可以的:
if(root==nullptr){
return;
}
这里 return;是退出该层递归的意思。
这里对二叉树的操作仅仅是push_back操作,在其他题中可以换为其他操作,换汤不换药。(比如修改值等)
复杂度分析:
1)时间复杂度:O(n) :每个结点都要被访问一次
2)空间复杂度:O(n) :在最坏的情况下(单支树,此时的深度为n),栈需要存储n个结点,以便后续操作。平均情况下是O(logn),是对数级复杂度(不要再说为啥不是log2n,因为复杂度里对数级统一写成了logn,一共就只有7种时间复杂度)
这里顺便插一句:前序遍历,中序遍历,后序遍历的时间复杂度都是一样的。这三种遍历,每一个结点都被走过了三次,前序遍历是在走的第一遍就进行了操作,中序遍历是在走的第二遍进行了操作,后序遍历是在走的第三次进行了操作。(每种遍历方法都是从根结点开始访问,但是不是首先处理根结点就不一定了 )
后面中序遍历和后续遍历的递归算法都差不多了,只是操作的位置插在前边,中间,后边的不同。我就不仔细一步步写了。
1.3前序遍历的迭代法
在之前的递归方法中,会自动实现栈的功能帮助我们保存函数的局部变量,参数值,地址等等。
这里使用迭代法,我们就自己模拟出一个栈,实现功能。
总体的过程如下:(也许我的字确实太烂了)

class Solution {
public:
vector<int> preorderTraversal(TreeNode* root) {
vector<int>res;
stack<TreeNode*>stk;
if(!root){
return res;
}
stk.push(root);//根结点放入之后,好戏就要开场了
while(!stk.empty()){
TreeNode* node = stk.top();
stk.pop();
res.push_back(node->val);//千万别把指针存进去了
if(node->right){
stk.push(node->right);
}
if(node->left){
stk.push(node->left);
}
}
return res;
}
};
迭代过程如下:
1.定义新结点,保存栈顶元素(指针)
2.弹出栈顶元素(指针)
3.栈顶元素放到最终的result容器中
4.依次放入此栈顶元素的右孩子和左孩子(如果哪一个没有就不放了)
1-4进行反复迭代,直到栈为空(所有元素都被弹了出去,且没有新的孩子进来)
这里需要注意的是需要先放右孩子,这是栈的先进后出机制所决定的。
复杂度分析:
迭代法的本质和递归法是一样的,通过栈来实现,所以复杂度一样
1)时间复杂度:O(n) :每个结点都要被访问一次
2)空间复杂度:O(n) :在最坏的情况下(单支树,此时的深度为n),栈需要存储n个结点,以便后续操作。平均情况下是O(logn)
二.中序遍历
2.1中序遍历的递归法
class Solution {
public:
void zhong(vector<int>& res,TreeNode* root){
if(!root){
return;
}
zhong(res,root->left);
res.push_back(root->val);
zhong(res,root->right);
}
vector<int> inorderTraversal(TreeNode* root) {
vector<int>res;
zhong(res,root);
return res;
}
};
1)时间复杂度:O(n) :每个结点都要被访问一次
2)空间复杂度:O(n) :在最坏的情况下(单支树,此时的深度为n),栈需要存储n个结点,以便后续操作。平均情况下是O(logn),是对数级复杂度(不要再说为啥不是log2n,因为复杂度里对数级统一写成了logn,一共就只有7种时间复杂度)
2.2中序遍历的迭代法
中序遍历的迭代法相比前序遍历的迭代法就没有那么简单了。
中序遍历迭代法的思维图如下所示:

然后我们来写程序
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
stack<TreeNode*>stk;
vector<int>res;
TreeNode* cul=root;//后面我会从我的角度分析为何要用专门开个指针来记录
if(!root){
return res;
}
while(cul!=nullptr||!stk.empty()){
if(cul!=nullptr){
stk.push(cul);
cul =cul->left;
}
else{//else不能去掉,否则每次循环都会执行下面几条语句,丧失了判断性
cul=stk.top();
res.push_back(cul->val);
stk.pop();
cul=cul->right;
}
}
return res;
}
};
相比于前序遍历和后续遍历最大的不同,就是多了一个遍历指针。
我当时就在纳闷,为什么不像前序遍历一样,直接在每次循环里使用TreeNode* node = stk.top();来保存呢。后面我想到了一些可能的原因:
因为是中序遍历,那么栈stack在完成对左子树的访问后,回到根结点时,此时的栈为空了。按照前序遍历栈不为空的循环条件,此时整个循环就会结束,就无法完成对右子树的访问和操作了。
但是新定义一个指针cul,不仅可以方便我们对二叉树进行操作,而且只要在循环条件里进行适当修改,就可以保证栈为空情况下,二叉树依然可以完成对右子树的遍历:这个条件就是指针cul不为空:
while(cul!=nullptr||!stk.empty()){
1)时间复杂度:O(n) :每个结点都要被访问一次
2)空间复杂度:O(n) :在最坏的情况下(单支树,此时的深度为n),栈需要存储n个结点,以便后续操作。平均情况下是O(logn)
三.后序遍历
3.1后序遍历的递归法
class Solution {
public:
void hou(vector<int>& res,TreeNode* root){
if(!root){
return;
}
hou(res,root->left);
hou(res,root->right);
res.push_back(root->val);
}
vector<int> postorderTraversal(TreeNode* root) {
vector<int>res;
hou(res,root);
return res;
}
};
1)时间复杂度:O(n) :每个结点都要被访问一次
2)空间复杂度:O(n) :在最坏的情况下(单支树,此时的深度为n),栈需要存储n个结点,以便后续操作。平均情况下是O(logn),是对数级复杂度(不要再说为啥不是log2n,因为复杂度里对数级统一写成了logn,一共就只有7种时间复杂度)
3.2后序遍历的迭代法
按理说后序遍历的迭代法也会和中序遍历的迭代法一样复杂,但其实后序遍历的迭代法只需要在前序遍历的基础上进行一定更改就可以完成了。
在前序遍历中,我们是先放右孩子后放左孩子到栈里:
if(node->right){
stk.push(node->right);
}
if(node->left){
stk.push(node->left);
}
最后我们输出的result 就是“中左右”的顺序
如果我们先放左孩子,后放右孩子:
if(node->left){
stk.push(node->left);
}
if(node->rightt){
stk.push(node->right);
}
最后我们输出的result 就是"中右左"的顺序
中右左再翻转一下,就变成了左右中,这不就是后序遍历的顺序吗,这就简单了。
这里需要用到容器的翻转操作:
reverse(res.begin(), res.end())
整体力扣代码如下:
class Solution {
public:
vector<int> postorderTraversal(TreeNode* root) {
vector<int>res;
stack<TreeNode*>stk;
if(!root){
return res;
}
stk.push(root);//根结点放入之后,好戏就要开场了
while(!stk.empty()){
TreeNode* node = stk.top();
stk.pop();
res.push_back(node->val);//千万别把指针存进去了
if(node->left){
stk.push(node->left);
}
if(node->right){
stk.push(node->right);
}
}
reverse(res.begin(),res.end());
return res;
}
};
1)时间复杂度:O(n) :每个结点都要被访问一次
2)空间复杂度:O(n) :在最坏的情况下(单支树,此时的深度为n),栈需要存储n个结点,以便后续操作。平均情况下是O(logn)
四.层序遍历
这里要求输出的是嵌套容器的容器(约等于二维数组,尽量能用容器就不用数组,很多题会报错)
vector<vector<int>>res;
同时,层序遍历是用一个队列来实现的。层序遍历的解题图解 如下:

最后完整的代码如下:
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
queue<TreeNode*>q;
vector<vector<int>>res;
if(!root){
return res;
}
q.push(root);
while(!q.empty()){
int length=q.size();
vector<int>res_small;//定义嵌套的小容器
for(int i=0;i<length;i++){
TreeNode* node=q.front();
q.pop();
res_small.push_back(node->val);
if(node->left){
q.push(node->left);
}
if(node->right){
q.push(node->right);
}
}
res.push_back(res_small);
}
return res;
}
};
1)时间复杂度:O(n) :每个结点都要被访问一次
2)空间复杂度:O(n) :在最坏的情况下(满二叉树),最后一排的元素个数为2^(h-1),h为二叉树的深度,所以就为O(n)这里我还是有点蒙逼,不知道这一步怎么推导出来的,ChatGPT的解释是:而空间复杂度为O(n)的原因是,队列的最大长度不会超过二叉树的节点个数,即为n。因此,队列在存储所有节点时,最大使用的空间为O(n)。因此,二叉树的层序遍历的空间复杂度为O(n)。
没写完的地方
二叉树的前三种遍历还有一种方法,空间复杂度只有O(1),下一次写