PAT（甲级）2022年春季考试

7-1 Simple Lie Detection

分数 20

Lie detection usually uses a set of prepared questions to ask the testee, and the result is obtained by analyzing the testee’s reactions. The more advanced technology uses a polygraph (测谎仪) to monitor the physical activities of the testee. Our simple polygraph here is to make a judgment by analyzing the characteristics of the answers to the questions.

First, we ask the testee to complete N multiple choice questions, each with a single answer. Each question has 8 options, which are represented by the lowercase English letters a-h. Then we can obtain a string of length N, consisting of only the lowercase English letters a-h. Score each string, and those whose score exceeds a certain threshold (阈值) T are judged as “suspected liars”. The scoring rules are as follows:

the string starts with an f has its score −2;

the string ends with an a has its score −1;

for every longest segment of answeres where the same letter is chosen for consecutive questions, if the segment length is larger than 5, the score is to +3;

if an a is immediately followed by e or h, the score is to −4;

for every longest segment of answeres where consecutively increasing letters are chosen to answer consecutive questions (such as abcd or defgh), if the segment length is larger than 3, the score is to +5.

Your job is to score the answers and make a judgement.

Input Specification:
Each input file contains one test case. For each case, the first line gives 3 positive integers N (6≤N≤100), the number of questions; T (≤100), the threshold for judging a liar; and K (≤100), the number of testees.

Then K lines follow, each gives the string of answers of a testee.

Output Specification:
For each testee, print in a line the total score of his/her answers. If the score exceeds the threshold, print !!! after the score.
Sample Input:

12 1 6
fghaebcdeddd
ahhhhhhgbaaa
cdefffffffff
fffffghecaaa
feeeeeeeegcb
aaaaaabbbbbb

Sample Output:

-1
-2
8!!!
-3
1
6!!!

AC代码：

#include
using namespace std;
// 30 minutes
int N, T, K;
int main(){
    cin >> N >> T >> K;
    for(int i=0; i<K; ++i){
        int score = 0;
        string str;
        cin >> str;
        int n = str.size();
        if(str[0] == 'f') score -= 2;
        if(str.back() == 'a') score -= 1;
        int consec = 0, inc = 0,j=0;
        while(j < n) {
            int k = j + 1;
            while (k < n && str[j] == str[k])++k;
            if(k-j > 5){
                score += 3;
                j = k;
            }
            else j++;
        }
        j = 0;
        while(j < n) {
            int k = j;
            while (k+1 < n && str[k+1] == str[k] + 1)++k;
            if(k-j >= 3){
                score += 5;
                j = k;
            }
            else j++;
        }
        for(int j=0; j < n; ++j){
            if(str[j] == 'a' && j+1 < n && str[j+1]=='e' )score -= 4;
            if(str[j] == 'a' && j+1 < n && str[j+1]=='h' )score -= 4;
        }
        if( consec >= 5 ) score += 3;
        cout << score << (score>T?"!!!\n":"\n");
    }
    return 0;
}

7-2 The First K Largest Numbers

The task is simple: find the first K largest numbers from a given sequence of N integers, and output them in descending order.

Input Specification:
Each input file contains one test case. For each case, the first line contains 2 positive integers N (≤10^6 ) and K (≤5). Then N integer keys (in the range [−2 30,2 30 ]) are given in the next line. All the numbers in a line are separated by a space.

Output Specification:
For each test case, print in descending order the Kth largest numbers.

All the numbers in a line must be separated by a space, and there must be no extra space at the beginning or the end of the line.

Sample Input 1:

10 4
40 25 60 -15 30 -21 80 -1 -5 27

Sample Output 1:

80 60 40 30

Sample Input 2:

4 5
23 -17 99 1

Sample Output 2:

99 23 1 -17

AC代码：

#include
using namespace std;
int N, K;
int main(){
    cin >> N  >> K;
    priority_queue<int> pque;
    for(int i=0,a; i<N; ++i){
        scanf("%d",&a);
        pque.push(a);
        if(pque.size()>200000){
            priority_queue<int> temp;
            int num = K+1;
            while(num--){
                temp.push(pque.top());
                pque.pop();
            }
            pque = temp;
        }
    }
    for(int i=0; i<K; ++i){
        if(pque.empty())break;
        if(i)cout << " ";
        cout << pque.top();
        pque.pop();
    }
    return 0;
}

7-3 Is It A Binary Search Tree - Again

分数 25
A Binary Search Tree (BST) is recursively defined as a binary tree which has the following properties:

The left subtree of a node contains only nodes with keys less than the node’s key.
The right subtree of a node contains only nodes with keys greater than or equal to the node’s key.
Both the left and right subtrees must also be binary search trees.
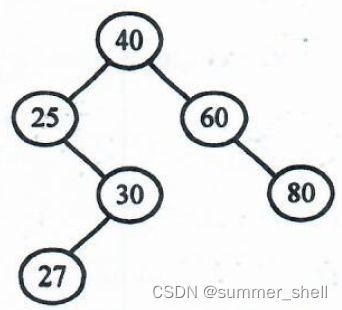
A binary tree with positive keys can be represented by an array, which stores the keys in level-order as in a complete tree, with all the NULL nodes represented by −1. For example, the following tree is stored in an array as { 40, 25, 60, -1, 30, -1, 80, -1, -1, 27 }.

Now given a sequence of integers in an array, you are supposed to tell if it corresponds to a BST, and output its inorder traversal sequence.

Input Specification:
Each input file contains one test case. For each case, the first line contains a positive integer N (≤1000). Then N integer keys (in the range (0, 100000)) are given in the next line. All the numbers in a line are separated by a space.

Output Specification:
For each test case, first print in a line YES if the sequence does correspond to a BST, or NO if not. Then print in the next line the inorder traversal sequence of that tree. It is guaranteed that the tree is non-empty.

All the numbers in a line must be separated by a space, and there must be no extra space at the beginning or the end of the line.

Sample Input 1:

10
40 25 60 -1 30 -1 80 -1 -1 27

Sample Output 1:

YES
25 27 30 40 60 80

Sample Input 2:

11
40 50 60 -1 30 -1 -1 -1 -1 -1 35

Sample Output 2:

NO
50 30 35 40 60

代码长度限制
16 KB
时间限制
400 ms
内存限制
64 MB

AC代码：

#include
#include
#include
#include
using namespace std;
int N;
vector<int>num;
bool fin = true;
void DFS(int cur){
    if(!fin || cur>=N || num[cur]==-1) return;
//    cout << num[cur] << endl;
    if(cur*2+1 < N && num[cur]<=num[cur*2+1] )fin = false;
    if(cur*2+2 < N && num[cur]>num[cur*2+2] )fin = false;
    DFS(cur*2+1);
    DFS(cur*2+2);
}
int tag = 0;
void Inorder(int cur){
    if(cur>=N || num[cur]==-1) return;
    //cout << num[cur]<
    Inorder(cur*2+1);
    if(tag++)printf(" ");
    printf("%d", num[cur]);
    Inorder(cur*2+2);
}
int main(){
    cin >> N;
    num.resize(N);
    for(int i=0,a; i<N; ++i){
        scanf("%d",&num[i]);
    }
    DFS(0);
    printf(fin?"YES\n":"NO\n");
    Inorder(0);
    return 0;
}

7-4 The Rescue
分数 30

Sample Input:

4 5
O#OOO
OOXOO
OO##O
OOO#O

Sample Output:

0011300121133

Hint:
During the 1st round, there are 3 candidates for A, as shown below:

O#OOO
OOXOO
OO##O
AOA#A

To direct them to X with the smallest sequence, we must choose the one at the lower-left corner, with the sequence 0011. Since at the very beginning, the hikers might be in any of the open areas, we apply 0011 to every open area, and obtain a map as shown below:

?#OO?
OOXO?
OO##O
OO?#O

where ? means that currently it is a possible position of the hikers. Now clearly we must pick the ? in the last row to be the next A, and direct it to X with 3001. After applying this sequence to other areas marked by ?, we update the map as the following:

?#OO?
OOXOO
OO##O
OOO#O

Now both ?'s have the same path length to X. We pick the upper-left corner to be A since it has the smaller sequence 211. The map is updated as the following:

O#OOO
OOXO?
OO##O
OOO#O

Finally apply 33, we can direct the last ? to X.

Hence the output sequence is 0011 3001 211 33.

代码长度限制
16 KB
时间限制
400 ms
内存限制
64 MB

烦事太多，出门一趟，回来截止提交了！！！