全国软考中级软件设计师 学习笔记-计算机组成原理部分
计算机组成原理
1.进制计算
1.1十进制转其他进制:展开计算
1.2其他进制转十进制:短除法再逆序书写
1.3二进制/八进制/十六进制换算:八进制三个一组、十六进制四个一组
注意:在十六进制中A代表10,B代表11 以此类推F代表15
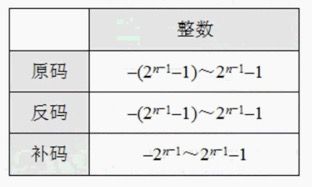
2.原码、反码、补码和移码
2.1 分别介绍以1 -1 和1-1的四种编码
2.2 原反补码的取值范围及解释补码多表示一个原因
补码能够多表示一个的原因是:在补码里+0和-0的补码相同,都是0000 0000
3. 浮点数计算
对阶->尾数计算->结果格式化
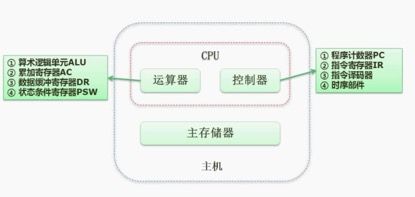
4. 计算机CPU结构
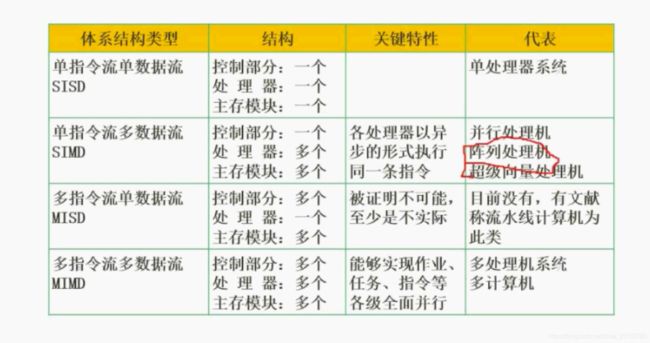
5.Flynn分类法
计算机体系结构分类方法
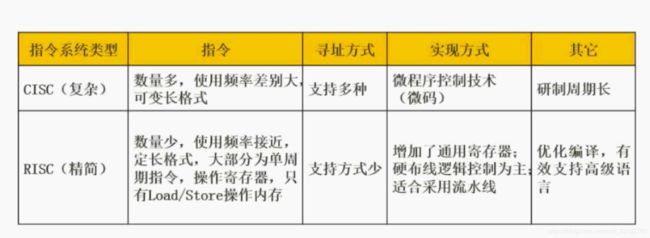
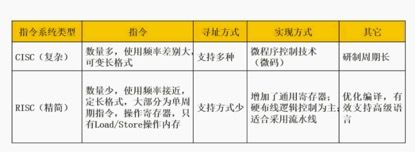
6. CISC与RISC
CISC(Complex Instruction Set Computers,复杂指令集计算集)和RISC(Reduced Instruction Set Computers)是两大类主流的CPU指令集类型,其中CISC以Intel,AMD的X86 CPU为代表,而RISC以ARM,IBM Power为代表。
7. 流水线
7.1 流水线概念
流水线包括三个部分
取指– 分析– 执行
7.2 流水线周期及执行时间
例题
流水线周期是最长的执行时间2ns
100条指令的理论执行完成时间= 2+2+1+(100-1)x 2 = 5+99x2= 203ns
100条执行的实际执行完成时间= (3+100-1)x2 = 102x2 = 204ns
注意:80%是指理论时间
7.3 流水线吞吐率
其最大吞吐率(忽略流水线准备时间)
7.4 流水线加速比
依旧对于本节例题
S = (2+2+1)x 100 /203 = 500 /203
7.5 流水线效率
其计算公式如下:
例题
E = (1+1+1+3)x 4 / (15 x 4) = 6 / 15 = 0.4
注意:1)对于相同时间片段的流水线其效率会较高
2)流水线上处理的任务越多,效率越高
3)处理相同数量任务,流水线片段越少,效率越高
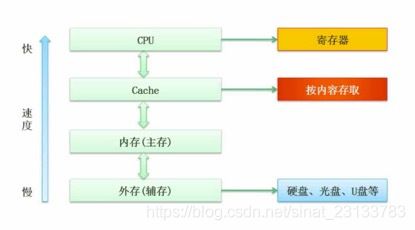
8. 计算机层次化存储结构
9. Cache
9.1 基本概念
当CPU同时使用Cache和主存时,计算公式
9.2 局部性原理
包括:时间局部性和空间局部性
工作集理论:工作集是进程运行时被频繁访问的页面集合
10. 主存
10.1 主存的分类
主存分为随机存储器与只读存储器
注意:1)随机存取存储器断电后内容被清除,而只读存储器可以保留
2)常见内存是随机存取存储器
10.2 主存编址
例题
- 1)先使用内存地址做减法:C7FFFH +1 – AC000H = 1C000H
注意:H代表十六进制
2)换算成十进制后再换算成K单位,除2^10:16^4 + 12*16^3 / 2^10 = 2^16 + 12*2^12 / 2^10 = 2^6 + 12*2^2 = 64 + 48 = 112
2. 利用第一问答案112K个地址单元
112K * 16 / (16K * 28) = 4
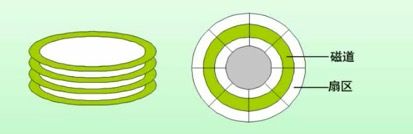
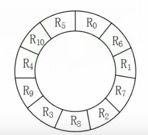
11. 磁盘
磁盘结构包括磁道和扇区
其存取时间如下:包括寻道时间和平均定位时间
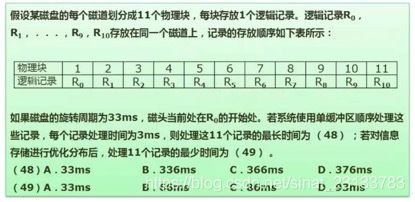
例题
- 从R0开始旋转读取后到达R1,但是因为是单缓冲区,此时R0还没有被处理,不能读取R1数据。当R0被处理后,此时磁头在R2,若要顺序处理R1,则需要等待再转回到R1。
由题可知,每个扇区读取时间为3ms,则从R0开始读取处理完成,将磁头转到下一个扇区,所需要时间为:33+3 = 36 ms
十个扇区完成此操作:36 * 10 = 360 ms
第十一个扇区读取和处理:360 + 3 + 3 =366 ms
- 当优化存储分布后,使得每个扇区数据被读取和处理后,磁头正好到达下一个扇区。
(3 + 3) * 11 = 66 ms
12. 计算机总线
根据总线所处的位置不同,总线通常被分成三种类型,分别是:
13. 串联和并联系统可靠性分析
13.1串联系统
设每个可靠度为R1,R2...Rn,则:
近似故障率为:
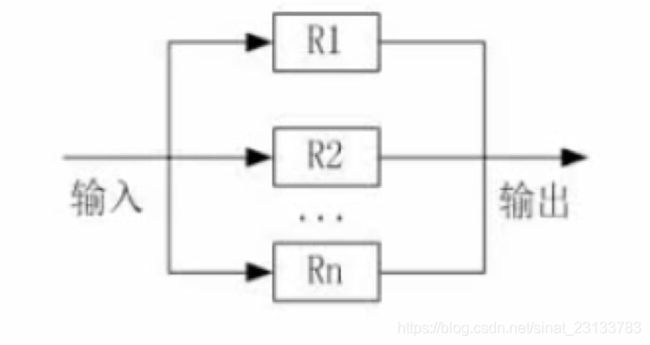
13.2 并联系统
设每个可靠度为R1,R2...Rn,则:
![]()
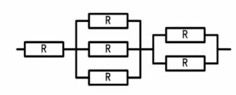
例题:混合系统
整体是一个串联系统,对于局部是并联系统,则依据计算公式:
14. 校验码
14.1 码距
一个编码系统的码距是整个编码系统中任意(所有)两个码子的最小距离
14.2 码距与检错和纠错关系
14.3 循环校验码CRC
可以进行检错但是不能够纠错的方法
模2除法:模2除法是指在做除法运算的过程中不计其进位的除法
1 )相同位数做除法,商1
2 )余数是异或运算的结果
例题
1)首先根据多项式,可以得出除数应为:11011
2)给原始报文末尾补多项式位数-1个0,即4个0
3)模2除法,异或运算
4)将最后的余数替换补0的数,就得到原始报文的CRC编码
计算过程如下所示:
14.4 海明校验码
例题:求信息1011的海明码
1)根据公式2^k >= n + k +1 计算出k位校验码由n=4 则k=3
| H7 |
H6 |
H5 |
H4 |
H3 |
H2 |
H1 |
| 1 |
0 |
1 |
(P3) |
1 |
(P2) |
(P1) |
分别在2^0=1 2^1=2 2^2=4 位置放置校验位
2 )将数据位对应的Hm中的m分别用二进制表示
| H3的3 |
0 |
1 |
1 |
| H5的5 |
1 |
0 |
1 |
| H6的6 |
1 |
1 |
0 |
| H7的7 |
1 |
1 |
1 |
| 将每列数值为1的元素做异或运算 |
P3 = 0 |
P2 = 0 |
P1 = 1 |
则最后海明码为:
| H7 |
H6 |
H5 |
H4 |
H3 |
H2 |
H1 |
| 1 |
0 |
1 |
0 |
1 |
0 |
1 |
3)若收到的信息为:1011101
| H7 |
H6 |
H5 |
H4 |
H3 |
H2 |
H1 |
| 1 |
0 |
1 |
1 |
1 |
0 |
1 |
S1 = H1 ⊕ H3 ⊕ H5 ⊕ H7 = 1 ⊕ 1 ⊕ 1 ⊕ 1 = 0
S2 = H2 ⊕ H3 ⊕ H6 ⊕ H7 = 0 ⊕ 1 ⊕ 0 ⊕ 1 = 0
S3 = H4 ⊕ H5 ⊕ H6 ⊕ H7 = 1 ⊕ 1 ⊕ 0 ⊕ 1 = 1 (错误)
说明由P3(H4)确定的那位结果出错了,H4取反即可得到正确的数据
参考链接:https://blog.csdn.net/weixin_42426249/article/details/89428080
想要电子版本的同学可以留言或者私信我获取,辛苦整理资料,欢迎点赞、收藏和评论!