代码随想录算法训练营第二天|LeetCode977.有序数组的平方、LeetCode209.长度最小的子数组、LeetCode59.螺旋矩阵Ⅱ

算法训练营打卡第二天，今天的前两道题目重点练习了双指针的用法，最后一道题目将边界条件的限定作为关键点，额外锻炼了逻辑能力。

LeetCode977.有序数组的平方

题目链接

https://leetcode.cn/problems/squares-of-a-sorted-array/

视频讲解

https://www.bilibili.com/video/BV1QB4y1D7ep

题目分析

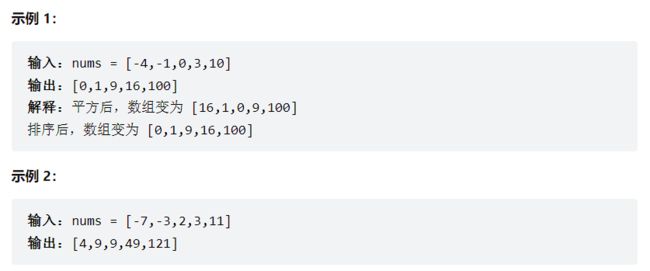
给你一个按 非递减顺序 排序的整数数组 nums，返回 每个数字的平方 组成的新数组，要求也按 非递减顺序 排序。

在手撕该题时，示例1的内容有给大家提供一种思路，根据解释的相关内容，我们只需要先将给定的nums数组平方，而后将平方后所得的数组进行排序即可。

因此，如何对所得数组进行快速的排序，就成为了解决这道题目的关键，在这里提供两种思路。

思路一：暴力求解

既然是对所得数组进行快速的排序，那么首先我们可以想到数据结构中涉及到的一系列排序方法，比如冒泡排序、快排、选择排序、插入排序、希尔排序等等，在这里我们选择快排进行排序，并在下面对快排的内容进行一些补充。

快速排序其实是对冒泡排序的一种补充，它的基本思想是：

通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据比另一部分的所有数据要小，再按这种方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，使整个数据变成有序序列。

在本文中不对快速排序的详细过程进行讲解，详细的题解大家可以翻阅下面这篇文档，讲的很奈斯~

传送门快速排序算法详解（原理、实现和时间复杂度） (biancheng.net)

阅读完文档的uu们可以知道，快速排序是一种不稳定的排序，它会由于待排数组的不同而耗费不同的时间（排列不同的次数）。但从平均意义的角度上来说，对于一个随机给定的数组，快排的效率是要优于其他排序方法的，因而对于一般情况下的排序问题，我们可以将快排作为首选的排序方式。

根据上文链接中讲述的相关方法，我们可以给出快排的第一种写法

 void QuickSort(int left, int right, vector& nums) {
        if(left < right) {
        int i = left, j = right;
        int standard = nums[left];
        while(i < j) {
            while(nums[j] > standard && i < j) {
                j--;
            }
            if(i < j) {
                int temp = nums[i];
                nums[i] = nums[j];
                nums[j] = temp;
                i++;
            }
            while(nums[i] < standard && i < j) {
                i++;
            }
            if(i < j) {
                int temp = nums[i];
                nums[i] = nums[j];
                nums[j] = temp;
                j--;
            } 
        }
        QuickSort(left, i - 1, nums);
        QuickSort(i + 1, right, nums);
        }
    }

上述代码中6-23行的代码就是文档中所提到的快排过程的具体体现。

选定一个基准数standard后，先从后往前比较（即移动j指针），若发现有数X比standard小，则将该数X与基准数交换位置，并开始从X的位置往后比较（即移动i指针），在往后移动i指针的过程中，若发现i指针所指数Y比基准数大，则将该数Y与基准数交换位置，并从Y的位置往前比较（即移动j指针）。以此推类，以i < j作为判定条件，进行循环。

比较完一组之后再基于前半部分、后半部分进行比较，因而有25、26行所写的递归形式。

而链接中所给出的快排写法将快排的步骤进行了一下简化，于是给出快排的第二种写法

void QuickSort(int left, int right, vector& nums) {
        if(left < right) {
        int i = left, j = right;
        int standard = nums[left];
        while(i < j) {
            while(nums[j] > standard && i < j) {
                j--;
            }
            if(i < j) {
                nums[i] = nums[j];
                i++;
            }
            while(nums[i] < standard && i < j) {
                i++;
            }
            if(i < j) {
               nums[j] = nums[i];
                j--;
            } 
        }
        nums[i] = standard;
        QuickSort(left, i - 1, nums);
        QuickSort(i + 1, right, nums);
        }
    }

此种写法不再将基准数与nums[i]或者nums[j]进行交换，而是直接根据大小进行相应位置的覆盖。最终i与j相等时，此时的位置即为基准数的位置，再将此时的位置用基准数覆盖即可。

在这种写法中，交换的次数比第一种写法中交换的次数要少很多，因而在力扣上运行时速度更快一些。

除此之外，我们还给出快排的第三种写法

void QuickSort(int left, int right, vector& nums) {
        if(left < right) {
        int i = left, j = right;
        int standard = nums[left];
        while(i < j) {
            while(i < j && nums[j] >= standard) {
                j--;
            }
            while(i < j && nums[i] <= standard) {
                i++;
            } 
            if(i < j) {
                int temp = nums[i];
                nums[i] = nums[j];
                nums[j] = temp;
            }
        }
        nums[left] = nums[i];
        nums[i] = standard;
        QuickSort(left, i - 1, nums);
        QuickSort(i + 1, right, nums);
        }
    }

在此种写法中，直接借助i（j）指针找出比基准数大（小）的数，然后将两指针所指向的数一次性进行交换，最终i与j相等时，退出循环；而后根据18、19行的相关操作，将基准数挪到正确的位置上，完成快排的实现。

对于第18、19行操作，我在理解时废了不少劲，最终觉得应该是这样子：

此种写法将基准数按住不动，只关注其他位置的数值，将其他位置的数值安排好后，再将第一位的基准数与第i（i=j）位数值进行交换即可。

可能还是理解的不太透彻，欢迎大家一起交流。

此种快排方式比较巧妙，且交换的次数更少，在力扣上运行速度更快，大家在理解的时候建议先根据第一种写法弄清楚基本过程，而后再钻研第二三种写法。

暴力求解中的关键点也就在于快排的实现，实现快排后再将给定数组平方一下然后利用快排函数处理一下就ok啦！

思路二：双指针法

该题利用双指针法还是非常容易的，只需要在平方后的数组的头尾处分别设置一个指针（记作i、j），同时额外开一个数组（大小和nums数组相同），两指针所指的数进行大小的比较后，哪个数大就先进入到所开数组的最大位置处，依次进行。最终将i、j指针相遇所指位置的数据填入到所开数组的0位置后，数组即为所求。

实现代码如下：

class Solution {
public:
    vector sortedSquares(vector& nums) {
        vector temp(nums.size());
        for(int i = 0; i < nums.size(); i++) {
            nums[i] = nums[i] * nums[i];
        }
        //定义变量存好数组nums的最大位置
        int boundary = nums.size() - 1;
        //在左右两头设定两个指针往里走，谁大谁先进入到temp的最大位置
        int left = 0;
        int right = nums.size() - 1;
        while(left != right) {
            if(nums[left] > nums[right]) {
                temp[boundary] = nums[left];
                boundary--;
                left++;
            }
            else {
                temp[boundary] = nums[right];
                boundary--;
                right--;
            }
        }
        temp[0] = nums[right];
        return temp;
    }
};

LeetCode209.长度最小的子数组

题目链接

https://leetcode.cn/problems/minimum-size-subarray-sum/

视频讲解

https://www.bilibili.com/video/BV1tZ4y1q7XE

题目分析

给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ，并返回其长度。如果不存在符合条件的子数组，返回 0 。

分析题目，需要找出总和 >= target的最小长度连续子数组，满足条件在于三个方面：

• 总和>=target

• 最小长度

• 连续

最直观的解法在于，从数组的第一个数开始，依次以第1、2、......、n个数作为起点然后逐渐扩大连续数组的长度，一旦满足>=target条件就停止扩大数组，此时满足最小长度的要求。依次循环，同时单独开一个resultLength变量储存最小长度值，根据循环结果不断进行更新。最终可以得出最小长度。

这种解法属于暴力解法，需要两个for循环嵌套，时间复杂度达到O（n2），在力扣上没法通过呜呜呜。

这里给一下代码

class Solution {
public:
    int minSubArrayLen(int target, vector& nums) {
        int ResultLength = INT32_MAX;
        for(int i = 0; i < nums.size(); i++) {
            int sum = 0;
            for(int j = i; j < nums.size(); j++) {
                sum += nums[j];
                if(sum >= target) {
                    int length = j - i + 1;
                    ResultLength = length < ResultLength ? length : ResultLength;
                    break;
                }
            }
        }
        return ResultLength == INT32_MAX ? 0 : ResultLength;
    }
};

灵活求解可以采用滑动窗口的方法，说白了还是双指针的问题。

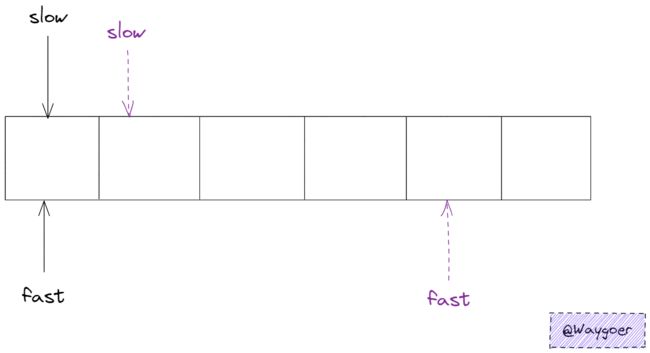
如图，定义两个指针，分别为快指针（fast）与慢指针（slow），快指针不断向后移动，并求取快指针与慢指针之间的所有数值之和，若快指针移动到某一位置时，求和>=target ，此时fast指针就可以停下来休息休息了，换慢指针往后移动，这一处理的目的就是在fast与初始位置之和恰好满足条件时，slow移动多少还能满足条件，由此可以得出在fast确定位置后所能有的最小长度。

对于整个过程来说，虽然涉及到fast和slow的移动，但是当fast移动到数组最末端的位置时，整个过程就基本结束。所以整体的时间复杂度只有O（n），故此种方法比暴力解法效率高得多。因为fast和slow移动的过程就像滑动的窗口一样，故名滑动窗口法。

代码滴滴~~

class Solution {
public:
    int minSubArrayLen(int target, vector& nums) {
        int sum = 0;
        int i = 0;
        int j = 0;
        int result = nums.size() + 1;
        int resL = 0;
        for(; j < nums.size(); j++) {
            sum += nums[j];
            while(sum >= target) {
                resL = j - i + 1;
                result = resL < result ? resL : result;
                sum -= nums[i];
                i++;
            } 
        }
        return result == (nums.size() + 1) ? 0 : result;
    }
};

注意，在这里最小长度result的初始选取应该大于nums.size()，这样才可以在后续窗口滑动时对最小长度result进行更新。也可以设置成INT32_MAX，意思是32位int类型变量的最大值，也就是21474836 47，正常情况下数组的长度是不能大于这个数的嗷~所以设置成这个肯定没问题。

LeetCode59.螺旋矩阵Ⅱ

题目链接

https://leetcode.cn/problems/spiral-matrix-ii/

视频讲解

https://www.bilibili.com/video/BV1SL4y1N7mV/

题目分析

给你一个正整数 n ，生成一个包含 1 到 n2 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。

转圈圈的题目，刚开始读题的时候可别犯迷糊偶~

注意，虽然示例中输出是一个数组，但我们需要做的不是去推导一个数字规律然后一行一行的按照顺序写进去，而是按照螺旋的方式确定每个数字在哪个方格然后移到那个方格，将数字写进去（数字都是有序的，在代码中处理的时候只要无脑++就可以）。

谁知道我读错题开始疯狂找规律有多痛苦呜呜呜（/(ㄒoㄒ)/~~）

那么这就回到我们熟悉的边界问题咯

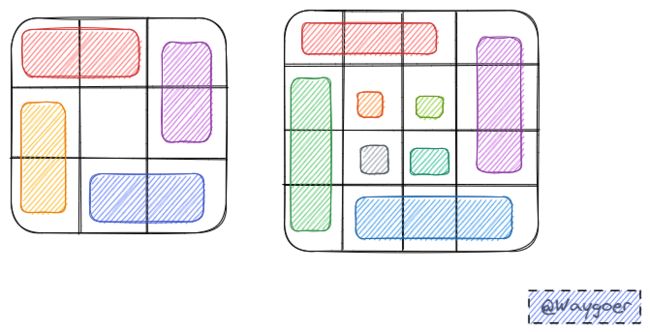
以一圈边界为例，我们需要让代码处理到任何一条边的时候都具有统一性，头尾处理与否对于每一条边来说都一致，这样子才能做到处理每一条边时都与前面一条边的处理情况相同，才能使用递归的方式进行循环处理。这么一想是不是简单多了~

以n=3和n=4为例：

在此我们选用左闭右开的区间类比即可。

代码贴贴~

class Solution {
public:
    vector> generateMatrix(int n) {
        int startx = 0;//设置初始循环位置的行坐标
        int starty = 0;//设置初始循环位置的列坐标
        int offset = 1;//设置初始循环的偏移值，此时采用左闭右开的方式，初始为一个偏移单位
        int i = 0;
        int j = 0;
        int count = 1;//待填入数组的元素
        int loop = n / 2;
        vector> Matrix(n, vector(n, 0));
        while(loop--) {
        for(j = starty; j < n - offset; j++) {
            Matrix[startx][j] = count++;//此处注意横坐标要设定为startx，不能设为i
            /*因为若有多重循环，则循环一遍后i位于第一遍循环的起始位置处，而第二遍循环应该从更新后的
            startx和starty处开始。
            要写成Matrix[i][j],则可在for循环的第一个条件中添加上“i = startx”。*/
        }
        for(i = startx; i < n - offset; i++) {
            Matrix[i][j] = count++;
        }
        for(;j > starty; j--) {
            Matrix[i][j] = count++;
        }
        for(; i >startx; i--) {
            Matrix[i][j] = count++;
        }
        startx++;
        starty++;
        offset++;
        }
    if(n % 2 == 1) {
        Matrix[n / 2][n / 2] = count++;
    }
    return Matrix;
    }
};

此代码中有三点需要注意：

• while的判定条件设定为loop--(loop = n / 2)，此时loop即为循环圈数。

• 代码最后应该根据n是奇数还是偶数确定是否需要给中间单独的一个方格进行赋值。

• 根据需要返回的变量类型，我们需要自己使用vector设置一个二维数组，这里的设置方法为

vector> Matrix(n, vector(n, 0));

注意vector设置二维数组的格式~~

总结

数组的整体内容到这里就告一段落啦！

统观这两天的内容，数组的考查方式大概有两种：

• 双指针变换

• 边界问题

掌握基本方法才能更好的应对纷繁复杂的变化偶~

还有一些拓展题型，之后会回来挑战的！

长度最小的子数组

• 904.水果成篮(opens new window)

• 76.最小覆盖子串

螺旋矩阵Ⅱ

• 54.螺旋矩阵

• 剑指Offer 29.顺时针打印矩阵

加油！！