算法导论 | 算法在计算中的作用
第一章 | 算法在计算中的作用
笔记
什么是算法?
- 算法就是任何良定义的计算过程,该过程取某个值或值的集合作为输入并产生某个值或值的集合作为输出
- 不正确的算法只要其错误率可控有时可能是有用的
- 算法的说明的唯一要求是这个说明必须精确描述所要遵循的计算过程
什么是数据结构?
- 数据结构是一种存储和组织数据的方式
什么是NP完全问题?
-
NP完全问题是指一类被认为在多项式时间内难以求解的问题。
具体来说,NP完全问题指的是所有可以在非确定性多项式时间(NP)内解决的问题,也就是说可以在多项式时间内验证一个解的正确性,但在多项式时间内却难以找到一个解。如果一个问题被证明为是NP完全问题,那么这个问题很可能是无法被高效解决的,因为在目前的算法研究中,还没有发现一种可以在多项式时间内解决所有NP完全问题的算法。
练习题
给出现实生活中需要排序的一个例子或者现实生活中需要计算凸壳1的一个例子
-
图书分类。图书馆中可能有数百万本书籍,它们需要按照特定的规则进行分类以方便读者查找。一种常见的分类方法是按照书的主题分类,比如历史、文学、科学等。对于每个主题,书籍需要按照作者、标题、出版日期等信息排序,以便读者可以快速找到自己需要的书籍。在这种情况下,需要对每个主题下的书籍进行排序,以便读者可以方便地找到需要的书籍。
-
航空管制。航空管制需要监视和管理空中飞行器的运动。航空器需要遵循特定的路径和航线,以保证安全和效率。凸壳可以用于确定航空器运动的边界,以便航空管制员可以更好地监视和管理它们。通过将所有飞机的位置投影到地图上,并计算它们的凸壳,航空管制员可以确定飞机的移动边界,从而更好地管理和协调航班。
除速度外,在真实环境中还可能使用哪些其他有关效率的量度?
- 空间复杂度:算法使用的内存空间也是一个非常重要的效率指标。在许多场景中,内存使用可能比计算时间更重要,因此优化算法的空间复杂度是很有意义的。
- 响应时间:某些场景下,算法必须能够实时响应,例如金融交易和游戏等。在这些情况下,算法的响应时间是非常重要的。
- 并发性:在一些应用场景中,同时处理多个请求是必要的。因此,算法的并发性也是一个重要的指标,它衡量算法在同时处理多个请求时的效率。
- 可维护性:算法的可维护性也是一个非常重要的指标,它衡量算法在代码调试、修复错误和添加新特性等方面的效率。高度可维护性的算法可以降低开发和维护成本,从而提高整体效率。
- 可扩展性:在某些场景中,算法必须能够适应不断增长的数据量和用户量。因此,算法的可扩展性也是一个重要的指标,它衡量算法在面对大规模数据和用户时的效率。
- ……
选择一种你以前已知的数据结构,并讨论其优势和局限
以数组为例。
优势:
- 随机访问:数组可以通过索引随机访问,也就是说可以直接访问任意元素,时间复杂度为O(1)。
- 连续的内存空间:数组中的元素在内存中是连续的,这意味着访问数组中的元素是非常快的。
- 内存缓存:由于数组的元素是连续的,所以当访问一个元素时,其周围的元素也会被加载到内存中,这种内存缓存可以提高访问效率。
- 容易实现:数组是一种非常简单和易于实现的数据结构,它只需要分配一段连续的内存空间即可。
劣势:
- 大小固定:数组在创建时需要指定大小,一旦创建后,大小就不能改变。如果需要动态调整数组的大小,就需要重新分配一段更大的内存空间,然后将原有的元素复制到新的空间中。
- 插入和删除效率低:如果需要在数组中插入或删除元素,就需要将插入或删除点之后的所有元素向后或向前移动,这个操作的时间复杂度为O(n)。
- 浪费内存空间:如果数组大小是固定的,而且使用不到数组的所有元素,这些空间就会浪费掉。在某些场景中,这种内存浪费可能是不可接受的。
- 数组索引下标易越界:数组下标越界是一个常见的错误,如果没有进行检查和处理,可能会导致程序崩溃或者产生不可预料的结果。
最短路径与旅行商问题有哪些相似之处,又有哪些不同?
最短路径问题和旅行商问题都是著名的图论问题,它们都是求解图中所有顶点对之间的最短路径或者一组顶点的最优遍历路径。下面是这两个问题的相似之处和不同之处:
相似之处:
- 都是图论问题:最短路径问题和旅行商问题都是图论中的经典问题,都涉及到在图中找到最优路径或最优遍历路径。
- 优化问题:最短路径问题和旅行商问题都是优化问题,需要找到满足一定条件下的最优解,例如最短路径或最优遍历路径。
不同之处:
- 问题目标不同:最短路径问题的目标是找到两个顶点之间的最短路径,而旅行商问题的目标是找到一条遍历所有顶点的最短路径。
- 算法复杂度不同:在完全图中,旅行商问题的时间复杂度是指数级的,而最短路径问题的时间复杂度是多项式级别的。
- 问题性质不同:最短路径问题是一个单源最短路径问题,它的目标是找到一个顶点到其他所有顶点的最短路径,而旅行商问题是一个TSP问题,需要找到一条遍历所有顶点的最短路径。
- 求解方法不同:最短路径问题可以使用经典的
Dijkstra算法或者Floyd算法求解,而旅行商问题则需要使用更加复杂的算法,例如贪心算法、动态规划或遗传算法等。
提供一个现实生活的问题,其中只有最佳解才行,然后提供一个问题,其中近似最佳的一个解也足够好
一个只有最佳解才行的现实生活问题是电路布线问题。在电路设计中,电路布线问题是一个非常重要的问题。它的目标是在给定的空间中,将电路中的各个元件之间的电线连接起来,使得电路性能最佳。这个问题的解必须是最佳的,因为如果电路布线出现错误,可能会导致电路性能下降,甚至损坏电路。
一个近似最佳的解也足够好的问题是货车路径规划问题。在现实生活中,物流公司需要规划货车的路径以最大化利润并最小化成本。虽然在理论上,最佳解是遍历所有可能路径以找到最短路径,但这是不现实的。因此,现实生活中,通常使用启发式算法来近似解决这个问题。即使是近似最佳的解决方案,也可以大大提高货车的效率并节省成本。
给出在应用层需要算法内容的应用的一个例子,并讨论涉及算法的功能
在应用层上的算法指的是在特定的应用中,根据应用需求和特点设计和实现的算法。这些算法通常用于解决特定领域中的问题,并与该领域的相关知识和实践相结合。
应用层算法的特点是:它们通常被设计用来解决具体问题,例如图像处理、语音识别、搜索引擎等。这些算法可以基于一些通用的算法技术进行设计,例如排序、搜索、图论等,但是在实践中它们会被优化和改进以适应特定的应用场景。
例如,在金融领域中,算法被广泛应用于股票预测、交易优化、信用风险评估等方面;在医疗领域中,算法被应用于医学影像处理、病理分析、药物设计等方面;在自然语言处理领域中,算法被应用于文本分类、机器翻译、情感分析等方面。
对规模为 n n n的输入,插入排序运行 8 n 2 8n^2 8n2步,而归并排序运行 64 n l g n 64nlgn 64nlgn步,请问对哪些 n n n值,插入排序优于归并排序?
假设插入排序的运行时间为 T 1 T_1 T1,归并排序的运行时间为 T 2 T_2 T2,则有:
T 1 = 8 n 2 T_1 = 8n^2 T1=8n2
T 2 = 64 n l o g n T_2 = 64nlogn T2=64nlogn
要求 T 1 < T 2 T_1 < T_2 T1<T2,即 8 n 2 < 64 n l o g n 8n^2 < 64nlogn 8n2<64nlogn。
将两边同时除以 8 n 8n 8n得到 n < 8 l o g n n < 8logn n<8logn,即插入排序优于归并排序的n的取值范围是 n < 8 l o g n n < 8logn n<8logn。
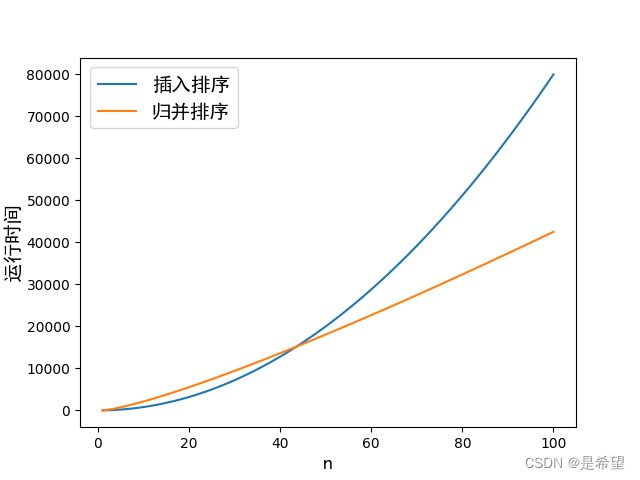
为了确定具体的取值范围,我们可以利用Python代码画出这两个函数的图像(详细代码参见附录A),如下所示:
可以看到,当 n ≤ 43 n \leq 43 n≤43 时,插入排序的运行时间小于归并排序的运行时间。因此,当 n n n的取值小于等于 43 43 43时,插入排序优于归并排序。
当 n > 43 n > 43 n>43 时,归并排序的运行时间逐渐超过插入排序的运行时间,因此,当 n n n大于 43 43 43时,归并排序优于插入排序。
n n n的最小值为多少时,运行时间为 100 n 2 100n^2 100n2 的一个算法在相同机器上快于运行时间为 2 n 2^n 2n的另一个算法
假设 T 1 = 100 n 2 T_1 = 100n^2 T1=100n2, T 2 = 2 n T_2 = 2^n T2=2n
要求 T 1 < T 2 T_1 < T_2 T1<T2,即 100 n 2 < 2 n 100n^2 < 2^n 100n2<2n。
为了确定具体的取值范围,利用Python代码画出这两个函数的图像(详细代码参见附录B),如下所示:
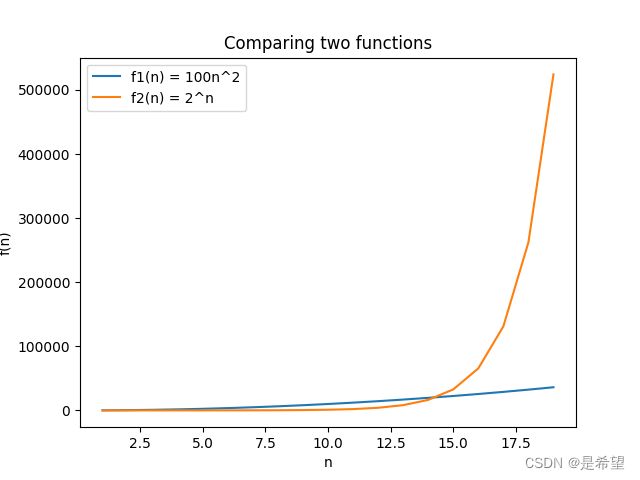
当 n 达到 14.26 时, 100 n 2 100n^2 100n2 和$ 2^n$ 的运行时间相等,此时 100 n 2 100n^2 100n2 的运行时间小于 2 n 2^n 2n。因此,在相同的机器上,当 n n n 大于 14.26 时,运行时间为 100 n 2 100n^2 100n2 的算法比运行时间为 2 n 2^n 2n 的算法更快。
思考题
假设求解问题的算法需要 f ( n ) f(n) f(n)毫秒,请对下表中的每个函数 f ( n ) f(n) f(n)和时间 t t t,确定可以在时间t内求解的问题的最大规模 n n n。
| 1秒钟 | 1分钟 | 1小时 | 1天 | 1月 | 1年 | 1世纪 | |
|---|---|---|---|---|---|---|---|
| l g n lgn lgn | 2 10 2^{10} 210 | 2 20 2^{20} 220 | 2 40 2^{40} 240 | 2 86 2^{86} 286 | 2 139 2^{139} 2139 | 2 200 2^{200} 2200 | 2 300 2^{300} 2300 |
| n \sqrt{n} n | 1 0 12 10^{12} 1012 | 3.6 × 1 0 15 3.6\times 10^{15} 3.6×1015 | 1.296 × 1 0 19 1.296\times 10^{19} 1.296×1019 | 6.5 × 1 0 21 6.5\times 10^{21} 6.5×1021 | 6.5 × 1 0 23 6.5\times 10^{23} 6.5×1023 | 3.15 × 1 0 26 3.15\times 10^{26} 3.15×1026 | 3.15 × 1 0 29 3.15\times 10^{29} 3.15×1029 |
| n n n | 1 0 6 10^6 106 | 6 × 1 0 7 6\times 10^7 6×107 | 3.6 × 1 0 9 3.6\times 10^9 3.6×109 | 8.64 × 1 0 10 8.64\times 10^{10} 8.64×1010 | 2.59 × 1 0 12 2.59\times 10^{12} 2.59×1012 | 3.15 × 1 0 13 3.15\times 10^{13} 3.15×1013 | 3.15 × 1 0 15 3.15\times 10^{15} 3.15×1015 |
| n l g n nlgn nlgn | 62746 62746 62746 | 267606 267606 267606 | 1.11 × 1 0 7 1.11\times 10^7 1.11×107 | 2.81 × 1 0 8 2.81\times 10^8 2.81×108 | 1.14 × 1 0 10 1.14\times 10^{10} 1.14×1010 | 1.8 × 1 0 11 1.8\times 10^{11} 1.8×1011 | 1.82 × 1 0 12 1.82\times 10^{12} 1.82×1012 |
| n 2 n^2 n2 | 1000 1000 1000 | 7745 7745 7745 | 60000 60000 60000 | 293938 293938 293938 | 1609968 1609968 1609968 | 5615692 5615692 5615692 | 5.623 × 1 0 7 5.623\times 10^7 5.623×107 |
| n 3 n^3 n3 | 100 100 100 | 391 391 391 | 1532 1532 1532 | 4420 4420 4420 | 13844 13844 13844 | 31593 31593 31593 | 146645 146645 146645 |
| 2 n 2^n 2n | 19 19 19 | 39 39 39 | 58 58 58 | 67 67 67 | 78 78 78 | 89 89 89 | 139 139 139 |
| n ! n! n! | 9 9 9 | 11 11 11 | 12 12 12 | 13 13 13 | 15 15 15 | 16 16 16 | 17 17 17 |
- l g n lgn lgn:基本思路是反复除以2直到得到1,该过程需要进行的次数就是 l o g 2 n log_2 n log2n,所以时间复杂度为 O ( l o g n ) O(log n) O(logn)。
- n \sqrt{n} n:该函数的时间复杂度为 O ( n ) O(\sqrt{n}) O(n),因为要计算的是 n n n的平方根,即需要进行的操作次数随着 n n n的增加而增加,但增加的速率比 n n n慢。
- n n n:时间复杂度为 O ( n ) O(n) O(n),因为算法需要对 n n n个元素进行线性扫描,每个元素需要常数级别的时间进行处理。
- n l g n nlgn nlgn:算法需要对 n n n个元素进行排序,排序算法的时间复杂度为 O ( n l o g n ) O(nlogn) O(nlogn)。
- n 2 n^2 n2:算法需要对 n n n个元素进行双重循环,所以时间复杂度为 O ( n 2 ) O(n^2) O(n2)。
- n 3 n^3 n3:算法需要对 n n n个元素进行三重循环,所以时间复杂度为 O ( n 3 ) O(n^3) O(n3)。
- 2 n 2^n 2n:算法需要进行指数级别的计算,所以时间复杂度为 O ( 2 n ) O(2^n) O(2n)。
- n ! n! n!:算法需要进行 n n n个元素的全排列,所以时间复杂度为 O ( n ! ) O(n!) O(n!)。
附录A
/*插入排序和归并排序比较 */
import matplotlib.pyplot as plt
import numpy as np
from matplotlib.font_manager import FontProperties
# 指定中文字体
font = FontProperties(fname=r'C:\Windows\Fonts\simhei.ttf', size=14)
# 定义函数
def f1(n):
return 8 * n**2
def f2(n):
return 64 * n * np.log2(n)
# 画图
n = np.arange(1, 101)
plt.plot(n, f1(n), label='插入排序')
plt.plot(n, f2(n), label='归并排序')
plt.xlabel('n', fontproperties=font)
plt.ylabel('运行时间', fontproperties=font)
plt.legend(prop=font)
plt.show()
附录B
/*同一台机器上,100n^2和2^n的比较 */
import matplotlib.pyplot as plt
import numpy as np
# 定义两个函数
def f1(n):
return 100 * n ** 2
def f2(n):
return 2 ** n
# 生成 n 的范围和对应的函数值
n = np.arange(1, 15)
y1 = f1(n)
y2 = f2(n)
# 画图
plt.plot(n, y1, label='f1(n) = 100n^2')
plt.plot(n, y2, label='f2(n) = 2^n')
# 图像标注
plt.xlabel('n')
plt.ylabel('f(n)')
plt.title('Comparing two functions')
plt.legend()
# 显示图像
plt.show()
在算法中,凸壳是指一个包含点集中所有点的最小凸多边形或凸包的边界。凸壳问题是计算机几何学中的基本问题,具有广泛的应用。凸壳问题可以用于诸如图像处理、计算机视觉、机器学习、自动化、地理信息系统等领域中。
像标注 ↩︎