机器学习-16-Semi-supervised Learning(半监督学习)

Semi-supervised Learning

半监督学习(semi-supervised learning)
1、introduction
2、Semi-supervised Learning for Generative Model
3、Low-density Separation Assumption：非黑即白
4、Smoothness Assumption：近朱者赤，近墨者黑
5、Better Representation：去芜存菁，化繁为简

Introduction

Supervised Learning：$(x^r,{\hat{y}}^r)$${}_{r=1}^R$

• training data中，每一组data都有input $x^r$和对应的output $y^r$

Semi-supervised Learning：$\{(x^r,{\hat{y}}^r){\}}_{r=1}^R$} + $\{x^u{\}}_{u=R}^{R+U}$

• training data中，部分data没有标签，只有input $x^u$

• 通常遇到的场景是，无标签的数据量远大于有标签的数据量，即U>>R

• semi-supervised learning分为以下两种情况：

  • Transductive Learning：unlabeled data is the testing data

    即，把testing data当做无标签的training data使用，适用于事先已经知道testing data的情况(一些比赛的时候)

    值得注意的是，这种方法使用的仅仅是testing data的feature，而不是label，因此不会出现“直接对testing data做训练而产生cheating的效果”

  • Inductive Learning：unlabeled data is not the testing data

    即，不把testing data的feature拿去给机器训练，适用于事先并不知道testing data的情况(更普遍的情况)

• 为什么要做semi-supervised learning？

  实际上我们从来不缺data，只是缺有label的data，就像你可以拍很多照片，但它们一开始都是没有标签的

Why semi-supervised learning help？

为什么semi-supervised learning会有效呢？

The distribution of the unlabeled data tell us something.

unlabeled data虽然只有input，但它的分布，却可以告诉我们一些事情

以下图为例，在只有labeled data的情况下，红线是二元分类的分界线

但当我们加入unlabeled data的时候，由于特征分布发生了变化，分界线也随之改变

semi-supervised learning的使用往往伴随着假设，而该假设的合理与否，决定了结果的好坏程度；比如上图中的unlabeled data，它显然是一只狗，而特征分布却与猫被划分在了一起，很可能是由于这两张图片的背景都是绿色导致的，因此假设是否合理显得至关重要

Semi-supervised Learning for Generative Model

Supervised Generative Model

事实上，在监督学习中，我们已经讨论过概率生成模型了，假设class1和class2的分布分别为$mea{n}_1=u^1,covarianc{e}_1=\Sigma$、$mea{n}_2=u^2,covarianc{e}_2=\Sigma$的高斯分布，计算出Prior Probability后，再根据贝叶斯公式可以推得新生成的x所属的类别

Semi-supervised Generative Model

如果在原先的数据下多了unlabeled data(下图中绿色的点)，它就会影响最终的决定，你会发现原先的$u,\Sigma$显然是不合理的，新的$u,\Sigma$需要使得样本点的分布更接近下图虚线圆所标出的范围，除此之外，右侧的Prior Probability会给人一种比左侧大的感觉(右侧样本点"变多"了)

此时，unlabeled data对$P(C_1),P(C_2),u^1,u^2,\Sigma$都产生了一定程度的影响，划分两个class的decision boundary也会随之发生变化

讲完了直观上的解释，接下来进行具体推导(假设做二元分类)：

• 先随机初始化一组参数：$\theta =\{P(C_1),P(C_2),u^1,u^2,\Sigma \}$

• step1：利用初始model计算每一笔unlabeled data $x^u$属于class 1的概率$P_{\theta }(C_1|x^u)$

• step2：update model

  如果不考虑unlabeled data，则先验概率显然为属于class1的样本点数$N_1$/总的样本点数$N$，即$P(C_1)=\frac{N_1}{N}$

  而考虑unlabeled data时，分子还要加上所有unlabeled data属于class 1的概率和，此时它们被看作小数，可以理解为按照概率一部分属于$C_1$，一部分属于$C_2$
  $$P(C_1)=\frac{N_1+{\sum }_{x^u}P(C_1|x^u)}{N}$$
  同理，对于均值，原先的mean $u_1=\frac{1}{N_1}\sum _{x^r\in C_1}{x}^r$加上根据概率对$x^u$求和再归一化的结果即可
  $$u_1=\frac{1}{N_1}\sum _{x^r\in C_1}{x}^r+\frac{1}{{\sum }_{x^u}P(C_1|x^u)}\sum _{x^u}P(C_1|x^u)x^u$$
  剩余的参数同理，接下来就有了一组新的参数${\theta }^{\prime }$，于是回到step1->step2->step1循环

• 理论上该方法保证是可以收敛的，而一开始给$\theta$的初始值会影响收敛的结果，类似gradient descent

• 上述的step1就是EM algorithm里的E，step2则是M

以上的推导基于的基本思想是，把unlabeled data $x^u$看成是可以划分的，一部分属于$C_1$，一部分属于$C_2$，此时它的概率$P_{\theta }(x^u)=P_{\theta }(x^u|C_1)P(C_1)+P_{\theta }(x^u|C_2)P(C_2)$，也就是$C_1$的先验概率乘上$C_1$这个class产生$x^u$的概率+$C_2$的先验概率乘上$C_2$这个class产生$x^u$的概率

实际上我们在利用极大似然函数更新参数的时候，就利用了该拆分的结果：
$$logL(\theta )=\sum _{x^r}log{P}_{\theta }(x^r)+\sum _{x^u}log{P}_{\theta }(x^u)$$

Low-density Separation Assumption

接下来介绍一种新的方法，它基于的假设是Low-density separation

通俗来讲，就是这个世界是非黑即白的，在两个class的交界处data的密度(density)是很低的，它们之间会有一道明显的鸿沟，此时unlabeled data(下图绿色的点)就是帮助你在原本正确的基础上挑一条更好的boundary

Self Training

low-density separation最具代表性也最简单的方法是self training

• 先从labeled data去训练一个model $f^{\ast }$，训练方式没有限制
• 然后用该$f^{\ast }$去对unlabeled data打上label，$y^u=f^{\ast }(x^u)$，也叫作pseudo label
• 从unlabeled data中拿出一些data加到labeled data里，至于data的选取需要你自己设计算法来挑选
• 回头再去训练$f^{\ast }$，循环即可

注：该方法对Regression是不适用的

实际上，该方法与之前提到的generative model还是挺像的，区别在于：

• Self Training使用的是hard label：假设一笔data强制属于某个class
• Generative Model使用的是soft label：假设一笔data可以按照概率划分，不同部分属于不同class

如果我们使用的是neural network的做法，${\theta }^{\ast }$是从labeled data中得到的一组参数，此时丢进来一个unlabeled data $x^u$，通过$f_{{\theta }^{\ast }}^{\ast }()$后得到$\left[\begin{array}{c}0.7\\ 0.3\end{array}\right]$，即它有0.7的概率属于class 1，0.3的概率属于class 2

• 如果此时使用hard label，则$x^u$的label被转化成$\left[\begin{array}{c}1\\ 0\end{array}\right]$
• 如果此时使用soft label，则$x^u$的label依旧是$\left[\begin{array}{c}0.7\\ 0.3\end{array}\right]$

可以看到，在neural network里使用soft label是没有用的，因为把原始的model里的某个点丢回去重新训练，得到的依旧是同一组参数，实际上low density separation就是通过强制分类来提升分类效果的方法

Entropy-based Regularization

该方法是low-density separation的进阶版，你可能会觉得hard label这种直接强制性打标签的方式有些太武断了，而entropy-based regularization则做了相应的改进：$y^u=f_{{\theta }^{\ast }}^{\ast }(x^u)$，其中$y^u$是一个概率分布(distribution)

由于我们不知道unlabeled data $x^u$的label到底是什么，但如果通过entropy-based regularization得到的分布集中在某个class上的话，那这个model就是好的，而如果分布是比较分散的，那这个model就是不好的，如下图所示：

接下来的问题是，如何用数值的方法来evaluate distribution的集中(好坏)与否，要用到的方法叫entropy，一个distribution的entropy可以告诉你它的集中程度：
$$E(y^u)=-\sum _{m=1}^5{y}_m^{u}ln(y_m^u)$$
对上图中的第1、2种情况，算出的$E(y^u)=0$，而第3种情况，算出的$E(y^u)=-ln(\frac{1}{5})=ln(5)$，可见entropy越大，distribution就越分散，entropy越小，distribution就越集中

因此我们的目标是在labeled data上分类要正确，在unlabeled data上，output的entropy要越小越好，此时就要修改loss function

• 对labeled data来说，它的output要跟正确的label越接近越好，用cross entropy表示如下：
  $$L=\sum _{x^r}C(y^r,{\hat{y}}^r)$$

• 对unlabeled data来说，要使得该distribution(也就是output)的entropy越小越好：
  $$L=\sum _{x^u}E(y^u)$$

• 两项综合起来，可以用weight来加权，以决定哪个部分更为重要一些
  $$L=\sum _{x^r}C(y^r,{\hat{y}}^r)+\lambda \sum _{x^u}E(y^u)$$
  可以发现该式长得很像regularization，这也就是entropy regularization的名称由来

Semi-supervised SVM

SVM要做的是，给你两个class的data，去找一个boundary：

• 要有最大的margin，让这两个class分的越开越好
• 要有最小的分类错误

对unlabeled data穷举所有可能的label，下图中列举了三种可能的情况；然后对每一种可能的结果都去算SVM，再找出可以让margin最大，同时又minimize error的那种情况，下图中是用黑色方框标注的情况

SVM paper：Thorsten Joachims, ”Transductive Inference for Text Classification using Support Vector Machines”, ICML, 1999

当然这么做会存在一个问题，对于n笔unlabeled data，意味着即使在二元分类里也有$2^n$种可能的情况，数据量大的时候，几乎难以穷举完毕，上面给出的paper提出了一种approximate的方法，基本精神是：一开始你先得到一些label，然后每次改一笔unlabeled data的label，看看可不可以让你的objective function变大，如果变大就去改变该label，具体内容详见paper

Smoothness Assumption

concepts

smoothness assumption的基本精神是：近朱者赤，近墨者黑

粗糙的定义是相似的x具有相同的$\hat{y}$，精确的定义是：

• x的分布是不平均的

• 如果$x^1$和$x^2$在一个high density region上很接近的话，那么${\hat{y}}^1$和${\hat{y}}^2$就是相同的

  也就是这两个点可以在样本点高密度集中分布的区域块中有一条可连接的路径，即 connected by a high density path

假设下图是data的分布，$x^1,x^2,x^3$是其中的三笔data，如果单纯地看x的相似度，显然$x^2$和$x^3$更接近一些，但对于smoothness assumption来说，$x^1$和$x^2$是处于同一块区域的，它们之间可以有一条相连的路径；而$x^2$与$x^3$之间则是“断开”的，没有high density path，因此$x^1$与$x^2$更“像”

digits detection

以手写数字识别为例，对于最右侧的2和3以及最左侧的2，显然最右侧的2和3在pixel上相似度更高一些；但如果把所有连续变化的2都放进来，就会产生一种“不直接相连的相似”，根据Smoothness Assumption的理论，由于2之间有连续过渡的形态，因此第一个2和最后一个2是比较像的，而最右侧2和3之间由于没有过渡的data，因此它们是比较不像的

人脸的过渡数据也同理

file classification

Smoothness Assumption在文件分类上是非常有用的

假设对天文学(astronomy)和旅行(travel)的文章进行分类，它们各自有专属的词汇，此时如果unlabeled data与label data的词汇是相同或重合(overlap)的，那么就很容易分类；但在真实的情况下，unlabeled data和labeled data之间可能没有任何重复的words，因为世界上的词汇太多了，sparse的分布很难会使overlap发生

但如果unlabeled data足够多，就会以一种相似传递的形式，建立起文档之间相似的桥梁

cluster and then label

在具体实现上，有一种简单的方法是cluster and then label，也就是先把data分成几个cluster，划分class之后再拿去训练，但这种方法不一定会得到好的结果，因为它的假设是你可以把同一个class的样本点cluster在一起，而这其实是没那么容易的

对图像分类来说，如果单纯用pixel的相似度来划分cluster，得到的结果一般都会很差，你需要设计一个很好的方法来描述image(类似Deep Autoencoder的方式来提取feature)，这样cluster才会有效果

Graph-based Approach

之前讲的是比较直觉的做法，接下来引入Graph Structure来表达connected by a high density path这件事

我们把所有的data points都建成一个graph，有时候建立vertex之间的关系是比较容易的，比如网页之间的链接关系、论文之间的引用关系；但有时候需要你自己去寻找vertex之间的关系

graph的好坏，对结果起着至关重要的影响，而如何build graph却是一件heuristic的事情，需要凭着经验和直觉来做

• 首先定义两个object $x^i,x^j$之间的相似度 $s(x^i,x^j)$

  如果是基于pixel的相似度，performance可能会不太好；建议使用autoencoder提取出来的feature来计算相似度，得到的performance会好一些

• 算完相似度后，就可以建graph了，方式有很多种：

  • k nearest neighbor：假设k=3，则每个point与相似度最接近的3个点相连
  • e-neighborhood：每个point与相似度超过某个特定threshold e的点相连

• 除此之外，还可以给Edge特定的weight，让它与相似度$s(x^i,x^j)$成正比

  • 建议用RBM function来确定相似度：$s(x^i,x^j)=e^{-\gamma ||x^i-x^j|{|}^2}$

    这里$x^i,x^j$均为vector，计算它们的Euclidean Distance(欧几里得距离)，加上参数后再去exponential

  • 至于加exponential，经验上来说通常是可以帮助提升performance的，在这里只有当$x^i,x^j$非常接近的时候，singularity才会大；只要距离稍微远一点，singularity就会下降得很快，变得很小

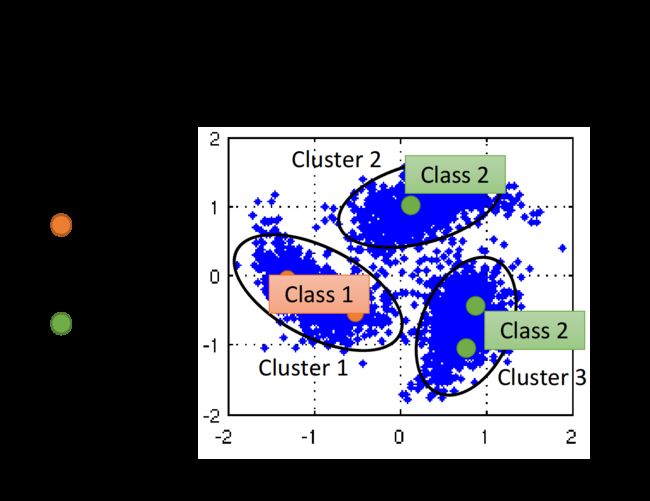
  • 使用exponential的RBM function可以做到只有非常近的两个点才能相连，稍微远一点就无法相连的效果，避免了下图中跨区域相连的情况

graph-based approach的基本精神是，在graph上已经有一些labeled data，那么跟它们相连的point，属于同一类的概率就会上升，每一笔data都会去影响它的邻居，而graph带来的最重要的好处是，这个影响是会随着edges传递出去的，即使有些点并没有真的跟labeled data相连，也可以被传递到相应的属性

比如下图中，如果graph建的足够好，那么两个被分别label为蓝色和红色的点就可以传递完两张完整的图；从中我们也可以看出，如果想要让这种方法生效，收集到的data一定要足够多，否则可能传递到一半，graph就断掉了，information的传递就失效了

介绍完了如何定性使用graph，接下来介绍一下如何定量使用graph

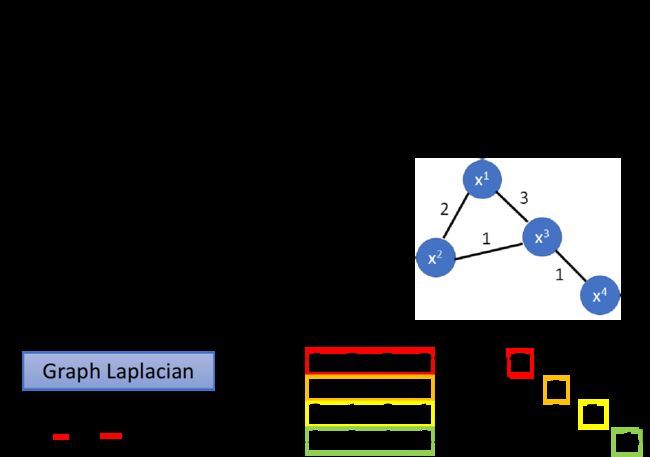
定量的使用方式是定义label的smoothness，下图中，edge上的数字是weight，$x^i$表达data，$y^i$表示data的label，计算smoothness的方式为：
$$S=\frac{1}{2}\sum _{i,j}{w}_{i,j}(y^i-y^j{)}^2$$
我们期望smooth的值越小越好

当然上面的式子还可以化简，如果把labeled data和unlabeled data的y组成一个(R+U)-dim vector，即
$$y={\left[\begin{array}{c}...y^i...y^j\end{array}\right]}^T$$
于是smooth可以改写为：
$$S=\frac{1}{2}\sum _{i,j}{w}_{i,j}(y^i-y^j{)}^2=y^{T}Ly$$
其中L为(R+U)×(R+U) matrix，成为Graph Laplacian， 定义为$L=D-W$

• W：把data point两两之间weight的关系建成matrix，代表了$x^i$与$x^j$之间的weight值
• D：把W的每一个row上的值加起来放在该行对应的diagonal上即可，比如5=2+3,3=2+1,…

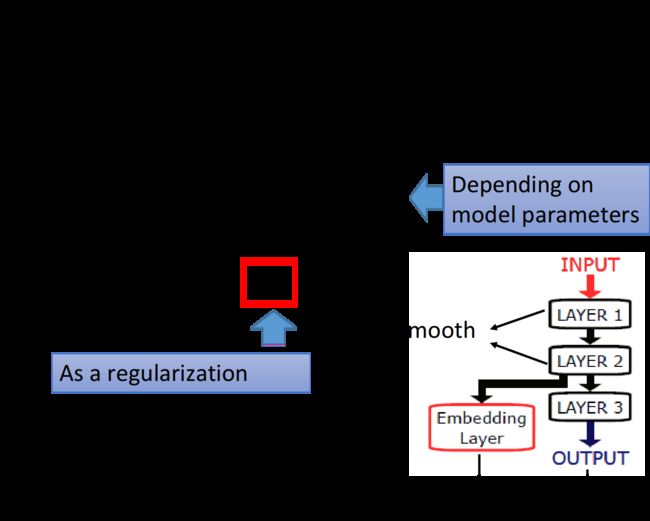
对$S=y^{T}Ly$来说，y是label，是neural network的output，取决于neural network的parameters，因此要在原来仅针对labeled data的loss function中加上这一项，得到：
$$L=\sum _{x^r}C(y^r,{\hat{y}}^r)+\lambda S$$
$\lambda S$实际上也是一个regularization term

训练目标：

• labeled data的cross entropy越小越好(neural network的output跟真正的label越接近越好)
• smooth S越小越好(neural network的output，不管是labeled还是unlabeled，都要符合Smoothness Assumption的假设)

具体训练的时候，不一定只局限于neural network的output要smooth，可以对中间任意一个hidden layer加上smooth的限制

Better Representation

Better Representation的精神是，去芜存菁，化繁为简

我们观察到的世界是比较复杂的，而在它的背后其实是有一些比较简单的东西，在操控着这个复杂的世界，所以只要你能够看透这个世界的假象，直指它的核心的话，就可以让training变得比较容易

举一个例子，在神雕侠侣中，杨过要在三招之内剪掉樊一翁的胡子，虽然胡子的变化是比较复杂的，但头的变化是有限的，杨过看透了这一件事情就可以把胡子剪掉。在这个例子中，樊一翁的胡子就是original representation，而他的头就是你要找的better representation

算法具体思路和内容到unsupervised learning的时候再介绍