模糊神经网络应用实例,神经网络和模糊控制

模糊神经网络的基本形式

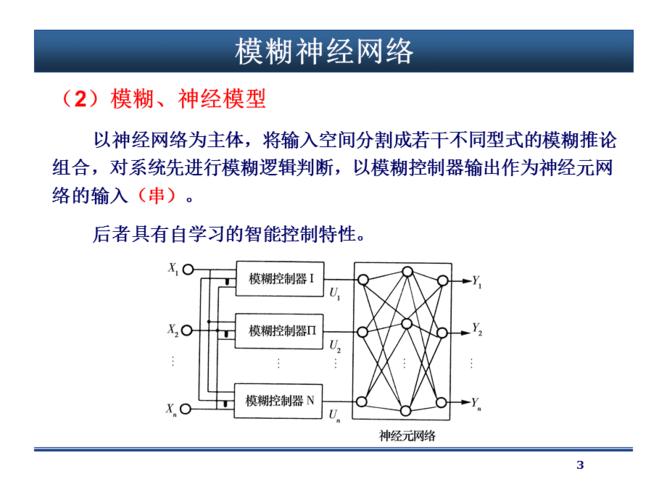
模糊神经网络有如下三种形式：1．逻辑模糊神经网络2．算术模糊神经网络3．混合模糊神经网络模糊神经网络就是具有模糊权系数或者输入信号是模糊量的神经网络。上面三种形式的模糊神经网络中所执行的运算方法不同。

模糊神经网络无论作为逼近器，还是模式存储器，都是需要学习和优化权系数的。学习算法是模糊神经网络优化权系数的关键。对于逻辑模糊神经网络，可采用基于误差的学习算法，也即是监视学习算法。

对于算术模糊神经网络，则有模糊BP算法，遗传算法等。对于混合模糊神经网络，目前尚未有合理的算法；不过，混合模糊神经网络一般是用于计算而不是用于学习的，它不必一定学习。

谷歌人工智能写作项目：小发猫

模糊神经网络的介绍

用matlab做模糊神经网络，步骤是什么？ 我知道模糊控制包括：模糊化，模糊推理，清晰化等步骤 20

简单介绍人工神经网络和模糊神经网络

其实百科介绍的很详细，如“人工神经网络是模拟人脑结构的思维功能，具有较强的自学习和联想功能，人工干预少，精度较高，对专家知识的利用也较少。

但缺点是它不能处理和描述模糊信息，不能很好利用已有的经验知识，特别是学习及问题的求解具有黑箱特性，其工作不具有可解释性，同时它对样本的要求较高;模糊系统相对于神经网络而言，具有推理过程容易理解、专家知识利用较好、对样本的要求较低等优点，但它同时又存在人工干预多、推理速度慢、精度较低等缺点，很难实现自适应学习的功能，而且如何自动生成和调整隶属度函数和模糊规则，也是一个棘手的问题。

”即保证人工神经网络自身的学习能力下，采用模糊理论解决模糊信号，使神经网络权系数为模糊权，或者输入为模糊量。

比如原本神经网络处理的是连续数据（double）不适合求解模糊数据，此时就需要引入模糊理论，来构造适合于求解这类模糊数据的神经网络。

模糊神经网络matlab

您好，是这样的：经过训练后的参数比较差，用原数据输入训练好的网络，得出结果和要的结果误差很大，不明白是怎么回事？还有要是多输入多输出这段程序该怎么改？模糊神经网络可以用matlab工具箱实现吗？

还有输入数据差别比较大（就是大小差异大）是不是要进行归一化再学习训练呢？求解，求解答！对于你的帮助不胜感激！

clearallclcclosealltic,%[x,y]=data;x=[12345678;-1-2-3-4-5-6-7-8];y=[23456789];%%%%%--数据显示，输入为－两输入，输出为－单输出。

--------样本为p2组[p1,p2]=size(x);%隶属度函数个数k=7;%初始化四个隶属度函数的参数A,B及输出层初始权值Wfori=1:p1;forj=1:k;m(i,j)=1+0.6*rand(1);b(i,j)=1+0.6*rand(1);endendforj=1:k*k;w(j)=1+rand(1);end%%%---推理计算输出值forq=1:p2;%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%-----用同一隶属度参数对输入样本X累计计算%选用高斯函数作为隶属度，求隶属度，共size(x,2)+k个。

x(1)K个，x(2)K个fori=1:p1;forj=1:k;u(i,j)=gaussmf(x(i,q),[m(i,j),b(i,j)]);endend%模糊推理计算：a21,a22.几个隶属度函数，得出几个值，此处已知输入为2%%%%----由以前的取小做法改为相乘—prod(x,1)orprod(x,2)———v=[];fori=1:kforj=1:kv=[v,u(1,i)*u(2,j)];endend%归一化计算模糊推理的值；相当于已经除去了经典去模糊输出的分母值fori=1:length(v);v1(i)=v(i)/sum(v);end%系统输出%out1(q)=w*v';%e(q)=(y(q)-out1(q));%end%out=out1out1(q)=w*v1';e(q)=y(q)-out1(q);endout=out1;%－三。

参数修正过程。

增加方式，非批处理方式迭代%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%－－－－－－－－---------------------误差反向传播过程－－－-----------------------------------------%取误差函数：E＝(1/2)*sumsqr(t-y)E=(1/2)*sumsqr(y-out);EE=E;%e=sum(y-out)lr=0.3;%c2=zeros(2,2);%%%%----------------------------------------误差反传后的参数修正过程-------------------r=1;%p=1;s=1000;%%e(r)=y(r)-out(r);whilep0.05%%%%%%%%%%%%%_____隶属度参数M.B输出层权值参数W的修正过程_____%%%%%%%%%%%%%%1.--Wwc=zeros(1,k*k);fori=1:k*k;wc(i)=-lr*e(r)*v1(i);end%%2.--Mmc=zeros(p1,k);fori=1:p1;forj=1:k;mc(i,j)=2*lr*e(r)*w(j)*(v(j)/u(i,j))*exp(-((x(i,r)-m(i,j)).^2)/(b(i,j).^2))*(x(i,r)-m(i,j))/(b(i,j).^2);endend%%3.--Bbc=zeros(p1,k);fori=1:p1;forj=1:k;bc(i,j)=2*lr*e(r)*w(j)*(v(j)/u(i,j))*exp(-((x(i,r)-m(i,j)).^2)/(b(i,j).^2))*((x(i,r)-m(i,j)).^2)/(b(i,j).^3);endend%4.参数修正mbwm=m-mc;b=b-bc;w=w-wc;%%%%%%%%%%%_______利用修正后的参数重新计算_____________%%%%%%%%%%%%%%%%%%%%%%5.利用修正过的参数重新计算输出forq=1:p2;fori=1:p1;forj=1:k;u(i,j)=gaussmf(x(i,q),[m(i,j),b(i,j)]);endendv=[];fori=1:7forj=1:7v=[v,u(1,i)*u(2,j)];endend%归一化计算模糊推理的值；相当于已经除去了经典去模糊输出的分母值fori=1:length(v)v1(i)=v(i)/sum(v);endout1(q)=w*v1';endout=out1;p=p+1;EE=(1/2)*sumsqr(y-out);E(p)=EE;r=r+1;ifr>p2r=1;ende(r)=(y(r)-out(r));end%%%%%%%%%%%%%%%%%%%________________当误差或迭代步数满足要求后得到结果_________________%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%m,b,w,E_out=EE,eepoch=1:size(E,2);figureplot(epoch,E,'-r');%plot(epoch,out(1),'b');%axis([01.5*smin(E)max(E)]);%set(gca,'fontsize',8);%set(gca,'xtick',0:s/10:1.5*s);%set(gca,'ytick',1e-30:1e5:1e5);%set(gcf,'color','b')title('误差变化曲线');xlabel('步数');ylabel('误差');toc%%%%泛化过程。

模糊推理的一般过程是什么?

matlab中自带的模糊神经网络如何操作的？

。

我上次发给你的程序，只要你从网上下一个matcom45就行了，直接装在c盘就可以了，你发给我的论文变量太多用一般的遗传算法不行，我从网上发现了一个PID神经网络，相当好用，不用计算隐层数目，很适合用遗传算法进行优化，我编了一个例程回来发给你。

我真的不会用matlab的工具箱，如果一定要用matlab来做优化，恐怕我帮不了你了。为什么一定要用matlab，用C++自己编写不也很好吗？

模糊神经网络

用MATLAB做的模糊神经网络代码

您好，是这样的：经过训练后的参数比较差，用原数据输入训练好的网络，得出结果和要的结果误差很大，不明白是怎么回事？还有要是多输入多输出这段程序该怎么改？模糊神经网络可以用matlab工具箱实现吗？

还有输入数据差别比较大（就是大小差异大）是不是要进行归一化再学习训练呢？求解，求解答！对于你的帮助不胜感激！

clearallclcclosealltic,%[x,y]=data;x=[12345678;-1-2-3-4-5-6-7-8];y=[23456789];%%%%%--数据显示，输入为－两输入，输出为－单输出。

--------样本为p2组[p1,p2]=size(x);%隶属度函数个数k=7;%初始化四个隶属度函数的参数A,B及输出层初始权值Wfori=1:p1;forj=1:k;m(i,j)=1+0.6*rand(1);b(i,j)=1+0.6*rand(1);endendforj=1:k*k;w(j)=1+rand(1);end%%%---推理计算输出值forq=1:p2;%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%-----用同一隶属度参数对输入样本X累计计算%选用高斯函数作为隶属度，求隶属度，共size(x,2)+k个。

x(1)K个，x(2)K个fori=1:p1;forj=1:k;u(i,j)=gaussmf(x(i,q),[m(i,j),b(i,j)]);endend%模糊推理计算：a21,a22.几个隶属度函数，得出几个值，此处已知输入为2%%%%----由以前的取小做法改为相乘—prod(x,1)orprod(x,2)———v=[];fori=1:kforj=1:kv=[v,u(1,i)*u(2,j)];endend%归一化计算模糊推理的值；相当于已经除去了经典去模糊输出的分母值fori=1:length(v);v1(i)=v(i)/sum(v);end%系统输出%out1(q)=w*v';%e(q)=(y(q)-out1(q));%end%out=out1out1(q)=w*v1';e(q)=y(q)-out1(q);endout=out1;%－三。

参数修正过程。

增加方式，非批处理方式迭代%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%－－－－－－－－---------------------误差反向传播过程－－－-----------------------------------------%取误差函数：E＝(1/2)*sumsqr(t-y)E=(1/2)*sumsqr(y-out);EE=E;%e=sum(y-out)lr=0.3;%c2=zeros(2,2);%%%%----------------------------------------误差反传后的参数修正过程-------------------r=1;%p=1;s=1000;%%e(r)=y(r)-out(r);whilep0.05%%%%%%%%%%%%%_____隶属度参数M.B输出层权值参数W的修正过程_____%%%%%%%%%%%%%%1.--Wwc=zeros(1,k*k);fori=1:k*k;wc(i)=-lr*e(r)*v1(i);end%%2.--Mmc=zeros(p1,k);fori=1:p1;forj=1:k;mc(i,j)=2*lr*e(r)*w(j)*(v(j)/u(i,j))*exp(-((x(i,r)-m(i,j)).^2)/(b(i,j).^2))*(x(i,r)-m(i,j))/(b(i,j).^2);endend%%3.--Bbc=zeros(p1,k);fori=1:p1;forj=1:k;bc(i,j)=2*lr*e(r)*w(j)*(v(j)/u(i,j))*exp(-((x(i,r)-m(i,j)).^2)/(b(i,j).^2))*((x(i,r)-m(i,j)).^2)/(b(i,j).^3);endend%4.参数修正mbwm=m-mc;b=b-bc;w=w-wc;%%%%%%%%%%%_______利用修正后的参数重新计算_____________%%%%%%%%%%%%%%%%%%%%%%5.利用修正过的参数重新计算输出forq=1:p2;fori=1:p1;forj=1:k;u(i,j)=gaussmf(x(i,q),[m(i,j),b(i,j)]);endendv=[];fori=1:7forj=1:7v=[v,u(1,i)*u(2,j)];endend%归一化计算模糊推理的值；相当于已经除去了经典去模糊输出的分母值fori=1:length(v)v1(i)=v(i)/sum(v);endout1(q)=w*v1';endout=out1;p=p+1;EE=(1/2)*sumsqr(y-out);E(p)=EE;r=r+1;ifr>p2r=1;ende(r)=(y(r)-out(r));end%%%%%%%%%%%%%%%%%%%________________当误差或迭代步数满足要求后得到结果_________________%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%m,b,w,E_out=EE,eepoch=1:size(E,2);figureplot(epoch,E,'-r');%plot(epoch,out(1),'b');%axis([01.5*smin(E)max(E)]);%set(gca,'fontsize',8);%set(gca,'xtick',0:s/10:1.5*s);%set(gca,'ytick',1e-30:1e5:1e5);%set(gcf,'color','b')title('误差变化曲线');xlabel('步数');ylabel('误差');toc%%%%泛化过程。