最近公共祖先问题四种常见解法
最近公共祖先问题
LCA定义
LCA指树中两个节点最近的一个公共祖先节点。
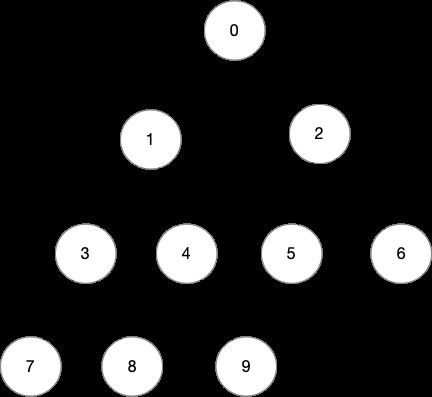
利用LCA可以求出树上任意两点之间的距离,假设树上所有节点到根节点的距离都存在dist数组里,则两个节点之间的距离为:dist[u]+dist[v]-2*dist[lca]
dist[0] = 0;
dist[1] = dist[2] = 1;
dist[3] = dist[4] = dist[5] = dist[6] = 2;
dist[7] = dist[8] = dist[9] = 3;
加入求解节点7和节点4之间的距离,利用上面的公式
dist[7]+dist[4] - 2*dist[1] = 3
结果正好和7到4之间的边数相同。
求解LCA
- 暴力搜索法
- 树上倍增法
- 在线RMQ算法
- 离线Tarjan算法
暴力搜索法
假设要求解u和v的最近公共祖先,暴力法有两种:
- 向上标记法
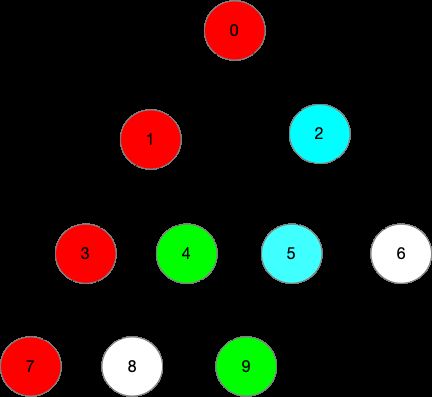
从其中任意一个节点出发,向根节点移动,移动的同时标记访的节点,访问到根节点停止。
从另一个节点出发向根节点移动,移动过程中遇到的第一个被标记的节点就是这两个节点的lca。
如图是分别查询了7和9,7和5的lca。
- 同步前进法
先选择两个节点中深度更深的一个节点,向上查询,直到和另一个节点深度相同。这时两个节点共同向上移动,共同查询到的第一个节点就是lca。
最坏时间复杂度
当树的形状是下面这样的时候,两种暴力算法都需要遍历所有树上的节点,时间复杂度为o(n)
树上倍增
创建ST表
F[i, j]代表i节点向上走2^j步到达的节点。
ST表的创建公式如下:
F[i, j] = F[F[i, j-1], j-1] 其中i是节点的名称,j的范围是0~log2(n),n是树上的节点数。
创建ST表的代码如下:
int n; // 树的节点数
int F[n+5][log2(n)+5];
void ST_create() {
int k = log2(n);
for (int j = 1; j <= k; ++j)
for (int i = 1; i <= n; ++i)
F[i, j] = F[F[i, j-1], j-1];
}
搜索
和暴力搜索的第二种方法类似,也是先让两个节点移动到同一深度,然后共同向上移动。唯一不同的就是向上移动时是按照倍增的思想移动的:
-
先尝试向上移动
2^k步,如果到达的节点的深度比另一个节点小,则不执行这次移动 -
再尝试向上移动
2^(k-1)步,如果到达的节点深度比另一个节点大,则执行移动 -
接着再次尝试向上移动
2^(k-2)步,按照上面的规则,如果到达节点深度大,则执行移动,否则不执行 -
直到尝试完
2^0步,这时两个节点的深度相同 -
两个节点同时向上移动,如果移动后到达同一个节点,则移动不执行,如果不为同一个节点则执行移动
-
重复上面的动作,每次尝试移动时都按照上面倍增的思想缩短移动步数,直到尝试完移动
2^0步 -
此时两个节点中任意一个的父节点就是他们的lca
下面是一种实现方法:
int LCA_st_query(int x, int y) {
if(d[x] > d[y])
swap(x, y);
for(int i = k; i >= 0; --i) {
if(d[F[y][i]] >= d[x])
y = F[y][i];
}
if(x==y) return x;
for(int i = k; i >= 0; --i) {
if(F[x][i] != F[y][i])
x = F[x][i], y = F[y][i];
}
return F[x][0];
}
在线RMQ算法
欧拉序列就是在深度遍历过程中记录下每次访问的节点,包括回溯。
在深度遍历过程中,任意两点之间的最短路径所经过的节点,一定在这两个节点首次出现在欧拉序之间的,所以这两个节点的公共祖先就是这些节点中深度最小的节点。
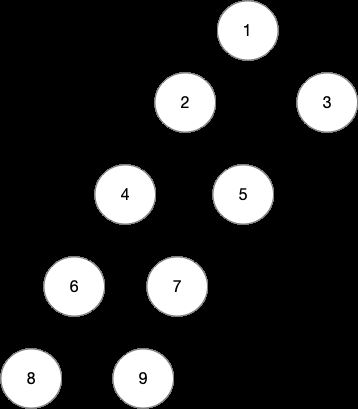
如有一棵树:
其欧拉序为:1 2 4 6 8 6 9 6 4 2 5 7 5 2 1 3 1
要想求节点8和5的lca,先找8和5在欧拉序中首次出现的位置,这两个位置之间深度最小的节点就是lca。
容易找到这两个位置及其之间的的数字为8 6 9 6 4 2 5,明显2是其中深度最小的节点,故其为这两个节点的lca。
得到欧拉序及相关参数
// pos[]存放首次出现的下标
// seq[]存放欧拉序列
// dep[]存放每个节点的深度
void dfs(int u, int d) { // u是当前访问的节点,d是当前节点的深度
vis[u] = true;
pos[u] = ++tot;
seq[tot] = u;
dep[tot] = d;
for(int i = head[u]; i; i = e[i].next) {
int v = e[i].to;
if(vis[v]) continue;
dfs(v, d+1);
seq[++tot] = u;
dep[tot] = d;
}
}
创建st表
void ST_create() { // F[i][j] 表示[i, i-1+2^j] 区间深度最小的节点下标
for(int i = 1; i <= tot; ++i)
F[i][0] = i;
int k = log2(tot);
for(int j = 1; j <= k; ++j)
for(int i = 1; i <= tot-(1<<j)+1; ++i)
if(dep[F[i][j-1]] < dep[F[i+(1<<(j-1))][j-1]])
F[i][j] = F[i][j-1];
else
F[i][j] = F[i+(1<<(j-1))][j-1];
}
查询[l, r]区间深度最小的节点下标
int RMQ_query(int l, int r) {
int k = log2(r-l+1);
if(dep[F[l][k]] < dep[F[r-(1<<k)+1][k]])
return F[l][k];
else
return F[r-(1<<k)+1][k];
}
查询lca
int LCA(int x, int y) {
int l = pos[x], r = pos[y];
if(l>r) swap(l, r);
return seq[RMQ_query(l, r)];
}
Tarjan算法
离线算法,一次性读入所有查询后再进行问题的求解。利用了并查集。
- 从根节点开始进行深度优先遍历,同时标记经过的节点
vis[p]=true; - 当某一节点
u的所有子节点被访问过之后,检查所有和u有关的查询,若存在一个查询u, v并且vis[v]==true;,则利用并查集查询v的祖宗,查询到的祖宗节点就是u, v的最近公共祖先。
int find(int x) {
if(x != fa[x])
fa[x] = find(fa[x]);
return fa[x];
}
void tarjan(int u) {
vis[u]=1;
for(int i = head[u]; i; i = e[i].next) { // 遍历当前节点的所有子节点,链式前向星存图
int v = e[i].to, w = e[i].c;
if(vis[v]) continue;
dis[v] = dis[u] + w;
tarjan(v);
fa[v] = u;
}
for(int i = 0; i < query[u].size(); ++i) {
int v = query[u][i];
int id = query_id[u][i];
if(vis[v]) {
int lca = find(v);
ans[id] = dis[u]+dis[v]-2*dis[lca];
}
}
}