排序——归并排序（递归/非递归）、计数排序

目录

归并排序

递归

单次

 整体

非递归

计数排序

---

归并排序

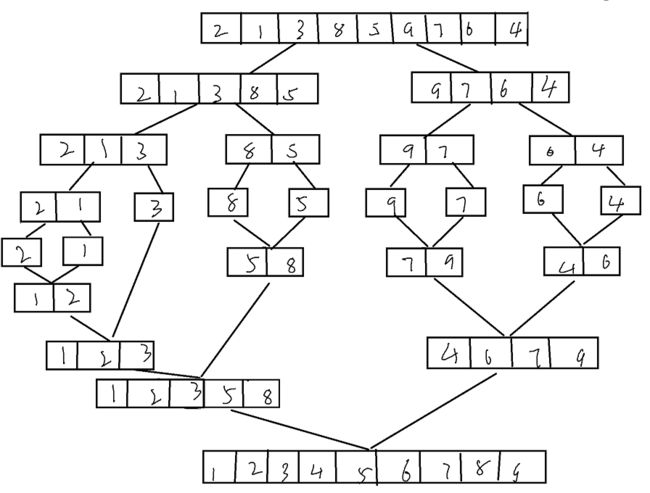
归并排序（MERGE-SORT）是建立在归并操作上的一种有效的排序算法,该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。

递归

单次

每次在我们写递归之前，我们都应该先将其单次的逻辑写出来

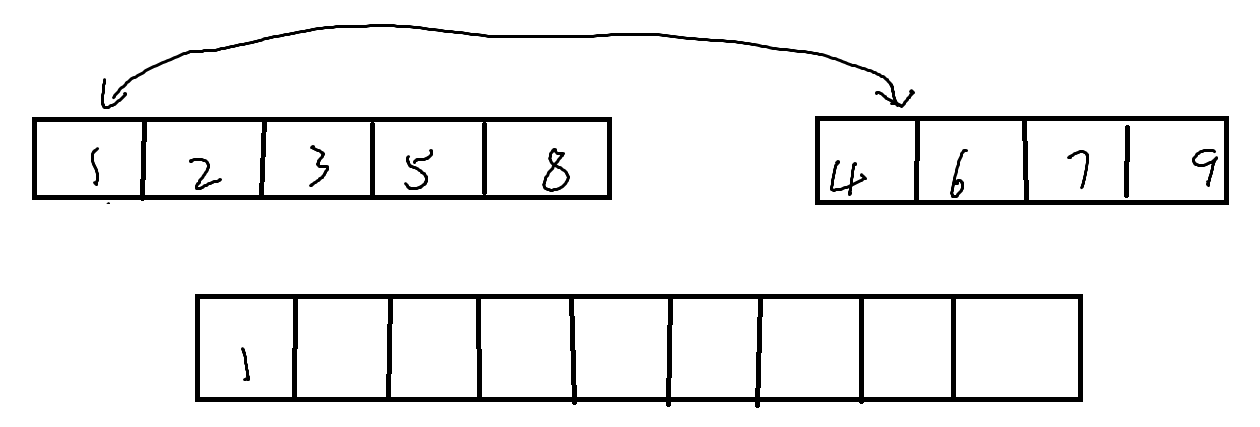
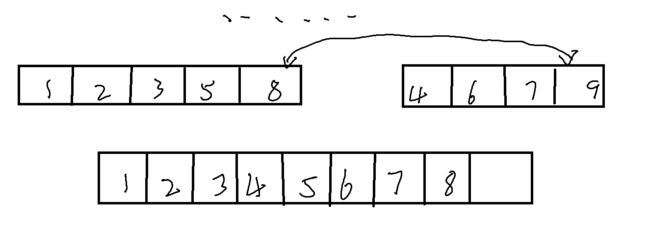
在单次中，我们要做的便是将有序（升序）的两个子序列合并为一个有序的序列。

由于我们要合并为一个新的序列，我们就需要一个空间来过渡地存储这个新的序列

	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		printf("malloc fail\n");
		exit(-1);
	}


	free(tmp);
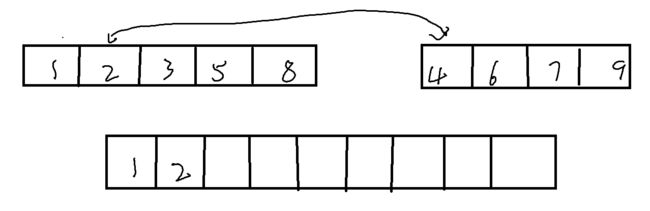
	tmp = NULL;

想要做到合并，我们可以比较两个子序列中最左侧的值相比较，之后将较小的一个数值放置在新的空间内。如此循环往复 

	if (left >= right)
		return;
	int mid = (left + right) / 2;
	int begin1 = left, end1 = mid;
	int begin2 = mid + 1, end2 = right;
	int i = left;
	while (begin1 <= end1 && begin2 <= end2)
	{
		if (a[begin1] < a[begin2])
		{
			tmp[i++] = a[begin1++];
		}
		else
		{
			tmp[i++] = a[begin2++];
		}
	}

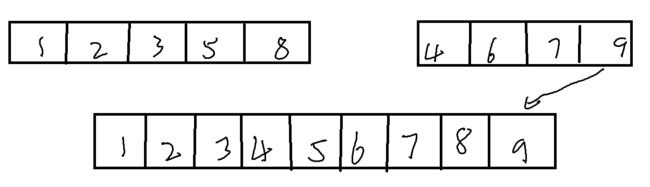
而当一个序列的数据被比较完毕后，另外一个序列一定会剩余一个或多个数据，而这一个或多个数据一定是比新空间内的数据都要大的，所以我们只需要将其一一放置进新的空间内。

while (begin1 <= end1)
{
	tmp[i++] = a[begin1++];
}

while (begin2 <= end2)
{
		tmp[i++] = a[begin2++];
}

 之后，我们便可以将这个新的序列放回原序列中

for (int j = left; j <= right; ++j)
{
	a[j] = tmp[j];
}

 整体

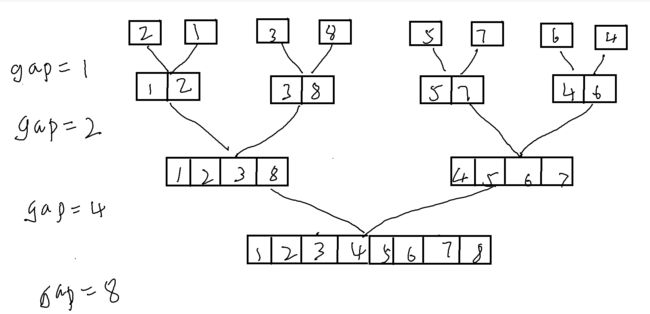
在我们最开始的图中，我们可以看到，在这个序列被划分的过程中，形似一个二叉树，因此我们可以采用与二叉树遍历类似的思想。而为了使子序列有序，我们首先进行的是最小区间之间的比较，即单个数据之间，因此，这也就像是后序遍历。

而每次向下递归，为了减小递归层数，我们可以使区间为中值及其左侧以及中值的右侧

如此，我们便可以很轻易的写出这个递归

void _MergeSort(int* a, int left, int right, int* tmp)
{
	if (left >= right)
		return;
	int mid = (left + right) / 2;
	int begin1 = left, end1 = mid;
	int begin2 = mid + 1, end2 = right;
	_MergeSort(a, begin1, end1, tmp);
	_MergeSort(a, begin2, end2, tmp);
	int i = left;
	while (begin1 <= end1 && begin2 <= end2)
	{
		if (a[begin1] < a[begin2])
		{
			tmp[i++] = a[begin1++];
		}
		else
		{
			tmp[i++] = a[begin2++];
		}
	}

	while (begin1 <= end1)
	{
		tmp[i++] = a[begin1++];
	}

	while (begin2 <= end2)
	{
		tmp[i++] = a[begin2++];
	}

	for (int j = left; j <= right; ++j)
	{
		a[j] = tmp[j];
	}
}

void MergeSort(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		printf("malloc fail\n");
		exit(-1);
	}

	_MergeSort(a, 0, n - 1, tmp);

	free(tmp);
	tmp = NULL;
}

---

非递归

首先，在第一次归并中，我们是将单个数据进行两两之间的归并，而之后，再次将归并好的数据进行再次两两归并，如此往复。

因此，我们不难想到，我们可以使用一个间距gap作为每个区间的大小，随着归并，将这个gap不断扩大，即变为2倍。这样，便能完成一个初步的思路。

而截至条件，显而易见，便是当gap>=n 

void MergeSortNonR(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int)*n);
	if (tmp == NULL)
	{
		printf("malloc fail\n");
		exit(-1);
	}
	
	int gap = 1;
	while (gap < n)
	{
		for (int i = 0; i < n; i += 2 * gap)
		{
			int begin1 = i, end1 = i + gap - 1;
			int begin2 = i+gap, end2 = i + 2*gap-1;
			int index = i;
			while (begin1 <= end1 && begin2 <= end2)
			{
	
				if (a[begin1] < a[begin2])
				{
					tmp[index++] = a[begin1++];
				}
				else
				{
					tmp[index++] = a[begin2++];
				}
			}
	
			while (begin1 <= end1)
			{
	
				tmp[index++] = a[begin1++];
			}
	
			while (begin2 <= end2)
			{
	
				tmp[index++] = a[begin2++];
			}
		}
			
		for (int i = 0; i < n; ++i)
		{
			a[i] = tmp[i];
		}
	
		gap *= 2;
	}
	
	free(tmp);
	tmp = NULL;
}

但以上的思路，有很大的局限性，它仅限于数组大小为2^n，否则end1、begin2、end2都有越界的可能。因此，我们需要对这三个点进行调整。

而越界存在着三种情况

1.end1、begin2、end2越界

2.begin2、end2越界

3.end2越界

当end越界时，其实比较好处理，我们只需要将end调整到不越界的位置（即n-1）。

而当begin2越界时，end2同样也是越界的，这时候我们不能将begin2也调整到不越界的位置，这样会导致begin2和end2中依旧存在一个数据，不合理，因此，我们可以将begin2和end2这个区间调整为不存在，由于end2越界会被调整到n-1，因此我们只需要将begin2调整到n即可。

void MergeSortNonR(int* a, int n)
{
	int* tmp = (int*)malloc(sizeof(int)*n);
	if (tmp == NULL)
	{
		printf("malloc fail\n");
		exit(-1);
	}
	
	int gap = 1;
	while (gap < n)
	{
		for (int i = 0; i < n; i += 2 * gap)
		{
			int begin1 = i, end1 = i + gap - 1;
			int begin2 = i+gap, end2 = i + 2*gap-1;
            //调整
			if (end1 >= n)
			{
				end1 = n - 1;
			}

			if (begin2 >= n)
			{
				begin2 = n;
				end2 = n - 1;
			}
	
			if (end2 >= n)
			{
				end2 = n - 1;
			}
            //结束调整
			int index = i;
			while (begin1 <= end1 && begin2 <= end2)
			{
	
				if (a[begin1] < a[begin2])
				{
					tmp[index++] = a[begin1++];
				}
				else
				{
					tmp[index++] = a[begin2++];
				}
			}
	
			while (begin1 <= end1)
			{
	
				tmp[index++] = a[begin1++];
			}
	
			while (begin2 <= end2)
			{
	
				tmp[index++] = a[begin2++];
			}
		}
			
		for (int i = 0; i < n; ++i)
		{
			a[i] = tmp[i];
		}
	
		gap *= 2;
	}
	
	free(tmp);
	tmp = NULL;
}

这样，我们便完成了归并排序的非递归情况。

---

---

计数排序

计数排序，是一种不用进行比较的排序，它的思想是在一个新的数组中统计所给数组中各个数据出现的次数，统计过后，进行排序。

例如这样一个数组  a[ ]={2,5,1,3,5,5,1}

在经过遍历后，我们得到 1出现两次，2出现一次，3出现一次，5出现三次

之后我们将其放置在一个数组中，数组的下标作为数据，下标表示的数据作为该下标出现的次数

即  count[ ]={0,2,1,1,0,3}

void CountSort(int* a, int n)
{
	int max = a[0], min = a[0];
	for (int i = 1; i < n; ++i)
	{
		if (a[i] > max)
		{
			max = a[i];
		}
	}
	int* count = (int*)malloc(sizeof(int) * max);
	memset(count, 0, sizeof(int) * max);
	if (count == NULL)
	{
		printf("malloc fail\n");
		exit(-1);
	}

	for (int i = 0; i < n; ++i)
	{
		count[a[i]]++;
	}

	int j = 0;
	for (int i = 0; i < max; ++i)
	{
		while (count[i]--)
		{
			a[j++] = i + min;
		}
	}
}

但当一个数组中每个数据都很大时

例如  a[ ]={1002,1005,1001,1003,1005,1005,1001}

便会产生很大程度上的空间浪费。因此，我们可以在第一次遍历中，找出最大值和最小值，得到range=max-min+1，之后创建的数组便可以为range，而对应的数据出现的次数便可以存储在该数据减去最小值的下标位置。

void CountSort(int* a, int n)
{
	int max = a[0], min = a[0];
	for (int i = 1; i < n; ++i)
	{
		if (a[i] > max)
		{
			max = a[i];
		}

		if (a[i] < min)
		{
			min = a[i];
		}
	}

	int range = max - min + 1;
	int* count = (int*)malloc(sizeof(int) * range);
	memset(count, 0, sizeof(int) * range);
	if (count == NULL)
	{
		printf("malloc fail\n");
		exit(-1);
	}

	for (int i = 0; i < n; ++i)
	{
		count[a[i] - min]++;
	}

	int j = 0;
	for (int i = 0; i < range; ++i)
	{
		while (count[i]--)
		{
			a[j++] = i + min;
		}
	}
}

这样我们便完成了计数排序

但我们要注意，的确这种方法的空间复杂度可以达到O(MAX(N,RANGE)),但这种排序方法使用场景比较有限，只适用于range较小（即数据较为集中的数组）。