读书笔记:“集体智慧编程”之第八章:对数值进行预测(构建价格模型)
数值预测的含义
在上一章节,我们接触到的决策树,比较适合对数据的分类进行预测,以及我们之前学过的分类器也是如此。但是当我们对数值型结果进行预测的时候应该怎么办呢?
具体什么叫做对数值型结果进行预测首先需要明确一下。比如:我们要在拍卖行竞价购买一个笔记本电脑,这台笔记本电脑有一些参数:处理器的速度,RAM的容量,硬盘的大小,屏幕的分辨率以及其他因素。显然,我们最终对其的定价必然要考虑这些参数,而这些参数的重要性各不相同,比如硬盘大小与屏幕大小相比,可能大家都觉得屏幕大小更为重要。那么各个因素都影响着我们最终对该款笔记本的最终的定价,这个定价就是我们所说的对数值型结果进行预测。我们可以使用第五章研究过的优化技术,求出最佳的权重。书中提出:- 贝叶斯分类器
- 决策树
- 支持向量机
都不是应对这种情况的最佳算法。本章将会研究如何应对这样的情况。
构建数据集
在我们构建数据集的时候,不得不注意这个数据集必须具有某些特征(也即是处理器速度、硬盘大小),而且这些特征最好比较复杂,使得价格比较难以预测。比如如果对电视机进行价格的预测,很显然屏幕越大,价格越高,那么这个预测实在是太简单了。
本书提出,构建的是一个葡萄酒价格的数据集。首先需要明确,酒的价格由两点决定,
- 等级
- 储藏的年代
请看代码:
from random import random,randint
import math
#rating代表酒的等级,age代表酒的年代。
def wineprice(rating,age):
#如果rating是代表酒的等级,同一等级的酒的峰值年是一样的。
#所以每一个峰值年是针对同一类等级的酒而言
peak_age=rating-50
#根据等级来计算价格
price=rating/2
if age>peak_age:
#经过“峰值年”之后,之后的5年,酒的品质会变差,价格降低
price=price*(5-(age-peak_age))
else:
#价格在接近“峰值年”时,会增加到原值的五倍
price=price*(5*(age+1)/peak_age)
if price<0:price=0
return price
执行代码,同一年等级的酒,不同的age:
print '(55,8):',wineprice(55,8)
print '(55,9):',wineprice(55,9)结果:
>>>
(55,8): 54
(55,9): 27
>>> 接着,我们来用代码产生葡萄酒价格的数据集,代码会随机产生200个普通酒的价格和年份,并且计算出其价格,然后随机加减20%,可以理解为是税收和价格的变动。
代码如下:
def winesetl():
rows=[]
for i in range(300):
#随机产生年代和等级
rating=random()*50+50
age=random()*50
#得到一个参考价格
price=wineprice(rating,age)
#增加“噪声”,也就是让酒的价格随机波动一下
price*=(random()*0.4+0.8)#这个写法很高端
#加入到数据集中
rows.append({'input':(rating,age),'result':price})
return rows有了数据集之后,我们就研究如何对一瓶新的普通酒进行价格预测。虽然,我们在构建数据集的时候使用了一个函数来计算出价格,我们心里也知道这个价格也许是虚构的,但是,现在请将数据集里产生的价格认为是真实的,这样,我们才能对一瓶新的普通酒进行价格预测,而不是直接用之前的函数wineprice()算出价格。
k-最近邻算法
上面一组,就代表了几个与新酒相似度的酒,这也是k的含义。那么到底选几个呢?这是值得探究的问题,显然选少了或者选多了都不是不行的。我们在实际运用时可以多试试不同的k值,也许会得到更为准确的结果。
如何确定两瓶酒相似呢?这里我们使用了应该是比较简单的算法:欧几里得算法
代码如下:
#用欧几里得来计算两瓶酒的相似度
def euclidean(v1,v2):
d=0.0
for i in range(len(v1)):
d+=(v1[i]-v2[i])**2
return math.sqrt(d)rows=winesetl()
print rows[0]
print rows[1]
print euclidean(rows[0]['input'],rows[1]['input'])>>>
{'input': (74.43448365296825, 14.861090558583973), 'result': 128.835924597139}
{'input': (75.15124316082637, 20.12510819860881), 'result': 152.09186781602241}
5.31259126101
>>>
有了相似度计算公式之后,我们很容易就能够计算出两瓶酒的相似度了,下面的代码是用于计算需要预测的新酒和数据集中的每一个的酒的距离(也就是相似度),算出来之后,我们才能排序,抽取出其中k个最相似度。注意,该函数的计算量比较大。
代码如下:#得到需要预测的新酒与数据集中所有酒的相似度
def getdistances(data,vec1):
distancelist=[]
for i in range(len(data)):
vec2=data[i]['input']
distancelist.append((euclidean(vec1,vec2),i))
distancelist.sort()
return distancelist拿到了新酒与所有酒的相似度,我们取出最相似的k个,算出这个k个酒的平均值,我们就得到了对新酒预测的价格:
def knnestimate(data,vec1,k=5):
#得到排序过后的相似度排序
dlist=getdistances(data,vec1)
avg=0.0
#对前k项结果求平均值
for i in range(k):
idx=dlist[i][1]#这里地方之所以是1的原因是取出在data列表里的序号
avg+=data[idx]['result']
avg=avg/k
return avg
执行代码:
rows=winesetl()
print knnestimate(rows,(95.0,3.0))结果:
>>>
25.3277961848
>>> 最相近的酒应该占有最大的比重
所以,我们要将得到相似度转化为权重。书中介绍了集中方式来完成这个功能:
inverse function
书中对这个词的翻译应该有错,书上想将的是y=1/x的这样的函数,却翻译为了反函数。
使用inverse function就可以完成将距离转换为权重这个过程。因为用欧几里得算出来的是两个点之间的距离,如果距离越大,那么其倒数就越小,如果距离越近,那么其倒数越大。这个方法有一个特点,就是如果非常近的话,那么占的权重非常之大,以至于会忽略掉相距稍稍有一点远的邻居,而且相距有点点远,但是它所在占的比重会下降的非常快。这到底是好事还是坏事,要看具体的项目有什么要求。代码如下:
#使用倒数来将距离转为权重
#const的存在是为了防止两点非常近,而导致了其距离非常近,倒数特别大,大到其他数都不起作用
def inverseweight(dist,num=1.0,const=0.1):
return num/(dist+const)减法函数
代码如下:
#用减法函数将距离转化为权重
def subtractweight(dist,const=1.0):
if dist>const:
return 0
else:
return const-dist高斯函数
代码如下:
#使用高斯函数将距离转化为权重
def gaussian(dist,sigma=10.0):
return math.e**(-dist**2/(2*sigma**2))测试三个函数的执行代码:
print inverseweight(0.1)
print subtractweight(0.1)
print gaussian(0.1)结果:
>>>
5.0
0.9
0.99995000125
>>> 加权kNN
代码:
def weightedknn(data,vec1,k=5,weightf=gaussian):
#得到距离值
dlist=getdistances(data,vec1)
avg=0.0
totalweight=0.0
#得到加权平均值
for i in range(k):
dist=dlist[i][0]
idx=dlist[i][1]
weight=weightf(dist)
avg+=weight*data[idx]['result']
totalweight+=weight
avg=avg/totalweight
return avg执行代码:
rows=winesetl()
print weightedknn(rows,(99.0,5.0))结果:
>>>
32.3515253922
>>> 交叉验证
这样有什么好处?就是验证我们的算法是否能够准确预测,而且我们可以对比使用不同的参数产生的结果,比如k的数量,比如到底是使用减法函数还是高斯函数来做距离转化为权重。
但是,我们这里并不是拿训练集去算法模型,而且用训练集去产生测试集中的一个预测的结果,比如knnestimate(data,vec1,k=5) 函数,其中的data传入的就是我们的训练集,vec1就是测试集中的一个。这是这一次算法的需要,但是我认为本质上还是没变的。
首先是把一个数据集划分为2个数据集,一个训练集和一个测试集,需要95%的训练集,5%的测试集。
代码如下:
#将数据拆分为训练集和测试集
def dividedata(data,test=0.05):
trainset=[]
testset=[]
for row in data:
if random()如果我们想突显偶尔出现一次很大的差距,使用差值的平方
如果我们关心每次与正确值的差距,而偶尔有一次很大的差距也无所谓,那么使用差值绝对值相加
测试算法的代码:
#测试算法的误差
#而是直接将训练集传入knnestimate函数,作为产生一个预测结果的基础,然后算出预测结果和真实结果之间的差距
def testalgorithm(algf,trainset,testset):
error=0.0
for row in testset:#这里只是拿testset来做个循环
guess=algf(trainset,row['input'])
error+=(row['result']-guess)**2#对数字求平方这样会突显其差距。
return error/len(testset)交叉测试的控制代码,从代码中,我们看出来了,并不是只做了一次拆分数据集和测试数据集代码的工作,我们是重复了100次,然后再取平均值。
代码如下:
def crossvalidate(algf,data,trials=100,test=0.05):
error=0.0
for i in range(trials):
trainset,testset=dividedata(data,test)
error+=testalgorithm(algf,trainset,testset)
return error/trials多执行几次代码,就可以得到如下结果:
>>> ================================ RESTART ================================
>>>
k=3时算法的误差: 534.299703506
k=3时算法的误差: 422.359768538
k=3时算法的误差: 460.892823922
k=3时算法的误差: 561.394791352
k=3时算法的误差: 438.566549999
>>> ================================ RESTART ================================
>>>
k=5时算法的误差: 356.420358448
k=5时算法的误差: 371.83561953
k=5时算法的误差: 299.178929108
k=5时算法的误差: 391.072240086
k=5时算法的误差: 352.400721703
>>> 变量的取值范围
rating=random()*50+50
age=random()*50
年代和等级都是一个是50到100,另一个是0到50,当我们利用这些数据算出两瓶酒的差距,也就是用欧几里得来算酒的相似度的时候,觉得不会有什么不妥。但是,下面当我们再加入一个新的变量,就是这个酒的毫升数。一般来说,葡萄酒的毫升数大约是330到1500。那么当我们再次计算酒的相似度的时候,就会由于毫升数的数值差距非常大,对最后的结果产生了更大的影响,使得其他变量发挥作用的能力小的多。如下图所示:
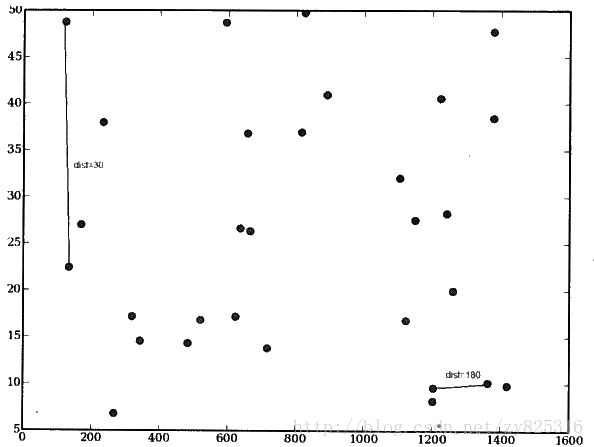
实际上,左边的连线,两点的距离更远,右边的连线两边的距离更近,从数值上来看,左边的才30,右边的都已经180了。显然,这会造成错误。
再来一种情况,比如说,我们在数据集中引入了完全与价格无关的变量,比如安放葡萄酒的通道号。当这个变量一起加入时,虽然实际上它不会对算法预测价格产生影响,但是算法还是认为这个变量会对价格带来影响,这样的话,算法预测的准确性就会大大降低。
那么我们如何应对这样在数值上差距很大和变量与价格预测无关的情况呢?
首先,让我们来生成本次要研究的特殊数据集。也就是多加个两个变量,酒的毫升数和酒的通道号。
代码:
def wineset2():
rows=[]
for i in range(300):
#随机产生年代和等级
rating=random()*50+50
age=random()*50
aisle=float(randint(1,20))#通道号
bottlesize=[375.0,750.0,1500.0,3000.0][randint(0,3)]#这个bottlesize的值会从第一个列表元素中选一个出来作为其值。
#得到一个参考价格
price=wineprice(rating,age)
price*=(bottlesize/750)
#增加“噪声”,也就是让酒的价格随机波动一下
price*=(random()*0.9+0.2)#这个写法很高端
#加入到数据集中
rows.append({'input':(rating,age,aisle,bottlesize),'result':price})
return rows执行代码:
rows=wineset2()
print '加入酒瓶大小和通道号后的误差:',crossvalidate(knnestimate,rows)结果:
>>>
加入酒瓶大小和通道号后的误差: 10510.9359299
>>> 应对策略:按比例缩放
也可以理解为归一化处理,我们不再使用变量实际的值去计算相似度,而是按比例缩放之后的数值。比如,我们把酒瓶的大小缩小10倍。如下图所示: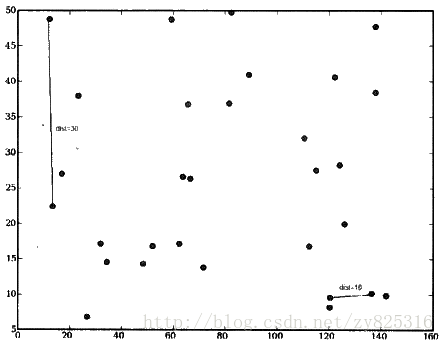
从上图我们看出,可以成功解决酒的毫升数天生数值比较大的问题。
那么对于通道号,我们能不能直接缩小为0倍呢?我们缩小了0倍试了一下:

可以看出,有效果,因为现在点之间的距离全靠y坐标来决定了。
下面写一个函数来完成按比例缩放
代码:
def rescale(data,scale):
scaleddata=[]
for row in data:
scaled=[scale[i]*row['input'][i] for i in range(len(scale))]#把里面每一次取出乘以相应的比例
scaleddata.append({'input':scaled,'result':row['result']})
return scaleddata执行代码:
rows=wineset2()
rdata=rescale(rows,[10,10,0,0.1])
print '缩放比例后的误差:',crossvalidate(knnestimate,rdata)结果:
>>>
缩放比例后的误差: 4737.15168622
>>> 缩放多少合适呢?
本次是我们自己设计的数据,我我们当然知道缩放多少比较合适,但是当我们缩放的数据不是我们设计时候,我们就不会知道缩放多少合适。我们还不知道这个变量是否能够缩放为0,也就是这个变量对价格有没有影响,我们完全不知道啊。对此,我们使用第五章学习过的优化算法来解决这个问题。优化过程需要我们提供的主要是3个参数:
- 变量的个数
- 变量划分的范围
- 成本函数
变量划分的范围是好多,我们可以定,树上定为0到20.也就是说每一个变量的缩放比例的范围都是0到20。
成本函数,很明显就是我们的交叉验证函数。
我们先来封装一个函数:
#封装一个成本函数。这是使用优化算法需要使用到的成本函数。
def createcostfuntion(algf,data):
def costf(scale):
sdata=rescale(data,scale)
return crossvalidate(algf,sdata)
return costfimport MyOptimization
data=wineset2()
costf=createcostfuntion(knnestimate,data)
weightdomain=[(0,20)]*4
print MyOptimization.annealingoptimize(weightdomain,costf,step=2)我们可以看出,经过优化函数可以得到每一个变量缩放比例,更为关键的是,我们看出哪些变量是完全没有用的,也就是缩放比例为0的那种。我们也能够看出那么变量是重要的,显然是那种缩放比例更大的变量。如果知道哪些变量缩放更大,我们就明白了,相对应的变量更为重要。
不对称分布问题
估计概率密度
如何应对这样的情况呢?在此之前,我们只是去取酒的邻居再算出其平均值,也就只是预测了其价格。现在,我们要知道这个酒的价格的区间是多少。也就是说,对于同一瓶酒:99%和20年,我们需要一个函数告诉我们,其价格位于40到80之间的概念是50%,价格介于80到100美元之间的概念也是50%。
为此,我们需要一个函数完成在这个功能,如下所示:
#给定一个价格区间,判断相应的酒在这个价格区间的概率
#为了更标准,也就是使用权重的方式
#在给定范围内的权重值,除以邻域内的所有权重值。
def probguess(data,vec1,low,high,k=5,weightf=gaussian):
dlist=getdistances(data,vec1)
nweight=0.0
tweight=0.0
for i in range(k):
dist=dlist[i][0]
idx=dlist[i][1]
weight=weightf(dist)
v=data[idx]['result']
#当前数据点位于指定范围内吗?如果是比例加1
if v>=low and v<=high:
nweight+=weight
tweight+=weight
if tweight==0:return 0
return nweight/tweight#告诉了我们比例是多少执行代码:
data=wineset3()
print '在40和80之间的概率:',probguess(data,[99,20],40,80)
print '在80和120之间的概率:',probguess(data,[99,20],80,120)
print '在120和1000之间的概率:',probguess(data,[99,20],120,1000)
print '在30和120之间的概率:',probguess(data,[99,20],30,120)
print '在0和100000之间的概率:',probguess(data,[99,20],0,100000)结果:
>>>
在40和80之间的概率: 0.195233597431
在80和120之间的概率: 0.385248220468
在120和1000之间的概率: 0.419518182101
在30和120之间的概率: 0.580481817899
在0和100000之间的概率: 1.0
>>> 上面的函数产生的结果确实非常具有参考价值,但是,如果总是让我们去猜,一个一个去试在哪个区间,再算出概率,必然呢也是一件非常
麻烦的事,所以我们需要一种能够获得整体概率分布的一种办法。
构建概率分布的图像
为了避免乱猜,我们使用一个图形化表达方式来绘制概率密度,这里有一个用于数学图形绘制的优秀软件:matplotlib。找到一个不错的下载python的windows函数库的网站。
注意,除了下载matplotlib,以外还要下载几个函数库才行。
累积概率
我们先构建之间概率图像,叫做:积累概率:显示结果小于给定值的概率分布的情况。我们从0开始,一个一个试,一直给定到概率为1.比如给定1000的时候概率为1了,表示价格0到1000的概率为1,那么也就知道这个酒的价格就是0到1000.具体的书写也非常简单,只需要与刚刚的probguess函数配合使用即可,代码如下所示:
from pylab import *
def cumulativegraph(data,vec1,high,k=5,weightf=gaussian):
t1=arange(0.0,high,0.1)#这里的arange()是定义一个数组,三个参数分别对应start, end, step
cprob=array([probguess(data,vec1,0,v,k,weightf)for v in t1])
plot(t1,cprob)#这个应该是t1是x坐标,cprob是y坐标
show()
执行代码:
data=wineset3()
cumulativegraph(data,(1,1),200)结果如图所示:
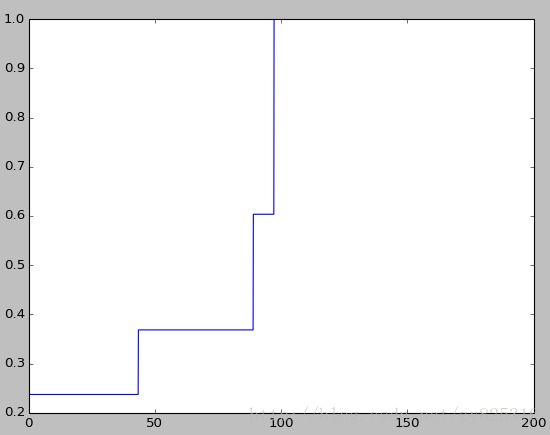
我们可以看到,在横坐标为0处的价格概率为0.24,说明有24%的价格为0。其次,可以看出在48处概率明显上升了,在98处概率达到1。这说明预测的价格的区间为0到98。我们也可以看出,比如区间在48到100的概率为0.74。仔细分析根据这幅图,我们可以得到更多的,价格区间的概率。
价格概率分布
代码如下:
#ss表示平滑程度
def probabilitygraph(data,vec1,high,k=5,weightf=gaussian,ss=5.0):
#首先建立价格范围,作为x轴
t1=arange(0.0,high,0.1)
#得到整个值域范围内的所有概率,注意范围只是0.1
probs=[probguess(data,vec1,v,v+0.1,k,weightf) for v in t1]
#通过加上近邻概率的高斯计算结果,做平滑处理
smoothed=[]
for i in range(len(probs)):
sv=0.0
for j in range(0,len(probs)):
dist=abs(i-j)*0.1
weight=gaussian(dist,sigma=ss)#距离越近,占的权重越大
sv+=weight*probs[j]
smoothed.append(sv)
smoothed=array(smoothed)
plot(t1,smoothed)
show()执行代码:
data=wineset3()
probabilitygraph(data,(95,8),150)结果:
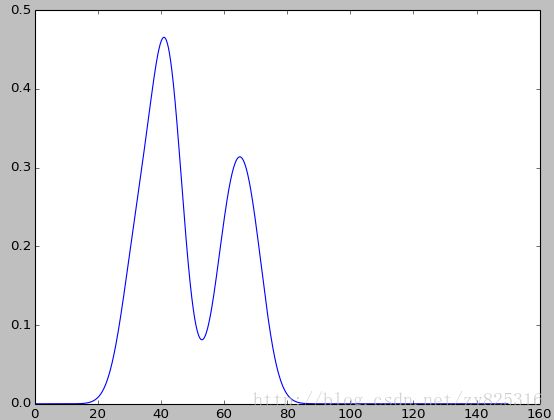
如上图所示,虽然有一点点,不那么准确,也就是不符合对于同一物品,价格相差一半。但是大概我们还是看的出,价格的概率坐落于两个区间,并且两个区间的价格大致上相差一半。符合我们设定的数据集,但是可能数据集的数量太少。不是特别标准。
有了上图,我们就可以更清楚的价格的坐落是有两个区间的,这对我们分析数据带来了一些启示。
总结
- 计算量大,因为要算每两点的距离
- 优化可以解决权重值问题,但是非常费时间
- 可以将新数据加入到数据集,并无需开销,因为我们知道权重
- 数据集中还有无法度量的元素的时候,我们可以建立概率函数。
对项目的启示
代码
# -*- coding: cp936 -*-
from random import random,randint
import math
#rating代表酒的等级,age代表酒的年代。
def wineprice(rating,age):
#如果rating是代表酒的等级,同一等级的酒的峰值年是一样的。
#所以每一个峰值年是针对同一类等级的酒而言
peak_age=rating-50
#根据等级来计算价格
price=rating/2
if age>peak_age:
#经过“峰值年”之后,之后的5年,酒的品质会变差,价格降低
price=price*(5-(age-peak_age))
else:
#价格在接近“峰值年”时,会增加到原值的五倍
price=price*(5*(age+1)/peak_age)
if price<0:price=0
return price
#模拟假设有一些酒是从折扣店,按照50%的价格购买的
#所以,我们需要将某些酒的价格降低一半
def wineset3():
rows=wineset1()
for row in rows:
if random<0.5:
#酒是从折扣店购买来的
row['result']*=0.5
return rows
def wineset2():
rows=[]
for i in range(300):
#随机产生年代和等级
rating=random()*50+50
age=random()*50
aisle=float(randint(1,20))#通道号
bottlesize=[375.0,750.0,1500.0,3000.0][randint(0,3)]#这个bottlesize的值会从第一个列表元素中选一个出来作为其值。
#得到一个参考价格
price=wineprice(rating,age)
price*=(bottlesize/750)
#增加“噪声”,也就是让酒的价格随机波动一下
price*=(random()*0.9+0.2)#这个写法很高端
#加入到数据集中
rows.append({'input':(rating,age,aisle,bottlesize),'result':price})
return rows
def wineset1():
rows=[]
for i in range(300):
#随机产生年代和等级
rating=random()*50+50
age=random()*50
#得到一个参考价格
price=wineprice(rating,age)
#增加“噪声”,也就是让酒的价格随机波动一下
price*=(random()*0.4+0.8)#这个写法很高端
#加入到数据集中
rows.append({'input':(rating,age),'result':price})
return rows
#用欧几里得来计算两瓶酒的相似度
def euclidean(v1,v2):
d=0.0
for i in range(len(v1)):
d+=(v1[i]-v2[i])**2
return math.sqrt(d)
#得到需要预测的新酒与数据集中所有酒的相似度
def getdistances(data,vec1):
distancelist=[]
for i in range(len(data)):
vec2=data[i]['input']
distancelist.append((euclidean(vec1,vec2),i))
distancelist.sort()
return distancelist
def knnestimate(data,vec1,k=5):
#得到排序过后的相似度排序
dlist=getdistances(data,vec1)
avg=0.0
#对前k项结果求平均值
for i in range(k):
idx=dlist[i][1]#这里地方之所以是1的原因是取出在data列表里的序号
avg+=data[idx]['result']
avg=avg/k
return avg
#使用倒数来将距离转为权重
#const的存在是为了防止两点非常近,而导致了其距离非常近,倒数特别大,大到其他数都不起作用
def inverseweight(dist,num=1.0,const=0.1):
return num/(dist+const)
#用减法函数将距离转化为权重
def subtractweight(dist,const=1.0):
if dist>const:
return 0
else:
return const-dist
#使用高斯函数将距离转化为权重
def gaussian(dist,sigma=10.0):
return math.e**(-dist**2/(2*sigma**2))
def weightedknn(data,vec1,k=3,weightf=gaussian):
#得到距离值
dlist=getdistances(data,vec1)
avg=0.0
totalweight=0.0
#得到加权平均值
for i in range(k):
dist=dlist[i][0]
idx=dlist[i][1]
weight=weightf(dist)
avg+=weight*data[idx]['result']
totalweight+=weight
avg=avg/totalweight
return avg
#将数据拆分为训练集和测试集
def dividedata(data,test=0.05):
trainset=[]
testset=[]
for row in data:
if random()=low and v<=high:
nweight+=weight
tweight+=weight
if tweight==0:return 0
return nweight/tweight#告诉了我们比例是多少
from pylab import *
def cumulativegraph(data,vec1,high,k=5,weightf=gaussian):
t1=arange(0.0,high,0.1)#这里的arange()是定义一个数组,三个参数分别对应start, end, step
cprob=array([probguess(data,vec1,0,v,k,weightf)for v in t1])
plot(t1,cprob)#这个应该是t1是x坐标,cprob是y坐标
show()
#ss表示平滑程度
def probabilitygraph(data,vec1,high,k=5,weightf=gaussian,ss=5.0):
#首先建立价格范围,作为x轴
t1=arange(0.0,high,0.1)
#得到整个值域范围内的所有概率,注意范围只是0.1
probs=[probguess(data,vec1,v,v+0.1,k,weightf) for v in t1]
#通过加上近邻概率的高斯计算结果,做平滑处理
smoothed=[]
for i in range(len(probs)):
sv=0.0
for j in range(0,len(probs)):
dist=abs(i-j)*0.1
weight=gaussian(dist,sigma=ss)#距离越近,占的权重越大
sv+=weight*probs[j]
smoothed.append(sv)
smoothed=array(smoothed)
plot(t1,smoothed)
show()
data=wineset3()
probabilitygraph(data,(95,8),150)
代码已经上传至网盘:
MyNumPredict.py
还使用了之前的代码:MyOptimization.py和数据集:schedule.txt