【刷题笔记】Day1:操作符的使用和算术转换

目录

操作符的使用

1.不允许创建临时变量，交换两个整数的内容

2.写一个函数返回参数二进制中 1 的个数。

方法1: 统计1的个数,遇到0跳过

方法2:右移操作符,&1得到最低为二进制最低位

方法3：n=n&(n-1)

3.获取一个整数二进制序列中所有的偶数位和奇数位分别打印出二进制序列

4.两个int(32位)整数m和n的二进制表达中,有多少个bit位不同?

方法1：m和n两者分别&1得到其二进制位最低位进行比较

方法2：异或之后使用:n=n&(n-1)

算术转换

1.编译器导致结果差异

2.sizeof的返回值类型

3.有序数列的合并

4.小乐乐走台阶

5.变种水仙花

6.三角形的判断

---

操作符的使用

1.不允许创建临时变量，交换两个整数的内容

这里用到^异或操作符:相异为1,相同为0
用到两个规律

1.a^a=0

2.a^0=a

整体思路:
a=3^3^5==0^5=5
异或是支持交换律的
为证明3^5^3==5
011-->3
101-->5
110--->中间值

    |
011-->3

    |

101-->5

#include
int main()
{
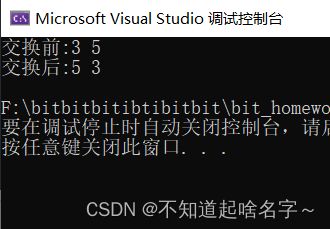
	int a = 3,  b = 5;
	printf("交换前:%d %d\n", a, b);
	a = a ^ b;
	b = a ^ b;//-->b=a^b^b==a^0=a
	a = a ^ b;//-->a=a^b^a==0^b=b
	printf("交换后:%d %d\n", a, b);
	return 0;
}

2.写一个函数返回参数二进制中 1 的个数。

比如： 15    0000 1111    4 个 1

思路:

方法1: 统计1的个数,遇到0跳过

//写一个函数返回参数二进制中 1 的个数。
//
//比如： 15    0000 1111    4 个 1
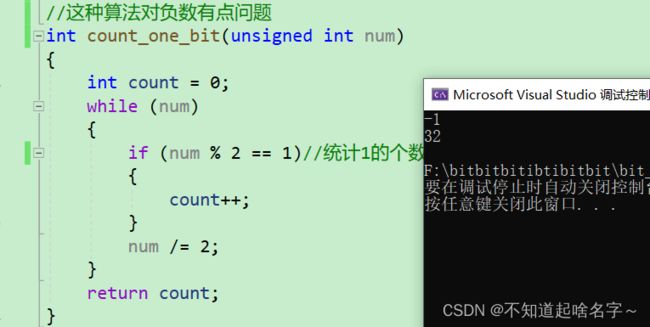
//这种算法对负数有点问题
int count_one_bit(int num)//这里要把 int 换成 unsigned int才能统计负数的1的个数
{
	int count = 0;
	while (num)
	{
		if (num % 2 == 1)//统计1的个数,遇到0跳过
		{
			count++;
		}
		num /= 2;
	}
	return count;
}
int main()
{
	int num = 0;
	scanf("%d", &num);
	int ret = count_one_bit( num);
	printf("%d\n", ret);
	return 0;
}

这个写法存在缺陷:

执行效果:

注意:当写成int类型的时候,用的时候是当成原码用的 

当把int num换成unsigned int num时

当num等于-1时

-1

10000000000000000000000000000001 -- 原码 —>我们日常生活中使用的

11111111111111111111111111111110  -- 反码

11111111111111111111111111111111  -- 补码

unsigned int 则认为-1补码全为有效位,不存在符号位,

方法2:右移操作符,&1得到最低为二进制最低位

int count_one_bit(int num)//这里参数无论unsigned int 还是int都能拿到每个bit位的&的结果
{
	int count = 0;
	int i = 0;
	for (i = 0; i < 32; i++)
	{
		if ((num >> i) & 1 == 1)//num是不会动的，不会改变num的值,下次回来循环的时候num的值还是原来的,变的只是i
		{
		count++; 
        }
	}
	return count;
}

方法3：n=n&(n-1)

int count_one_bit(int num)
{

	int count = 0;
	while (num)//只要num不为0,num里面就存在1
	{
		num = num & (num - 1);//去掉一个1
		count++;
	}
	return count;
}

原理:

题目类型:接口型和oj型,oj的意思是在线判题 

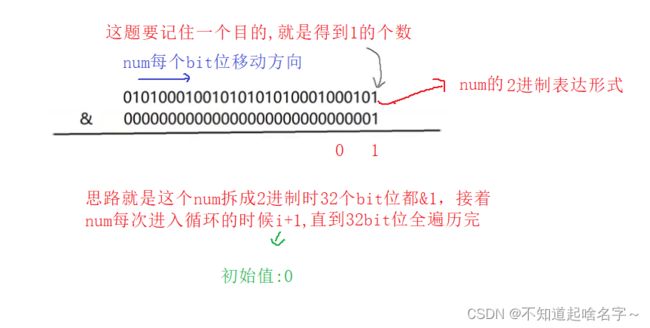
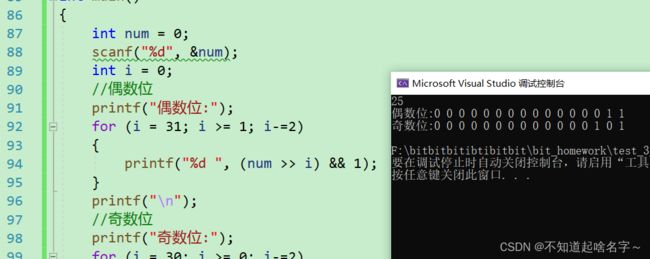
3.获取一个整数二进制序列中所有的偶数位和奇数位分别打印出二进制序列

方法:偶数位和奇数位的最高位和最低位到整个bit位最低位的距离

//记住:获得一个数的最低位，&1就可以了
//获取一个整数二进制序列中所有的偶数位和奇数位，分别打印出二进制序列
//1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
#include
int main()
{
	int num = 0;
	scanf("%d", &num);
	int i = 0;
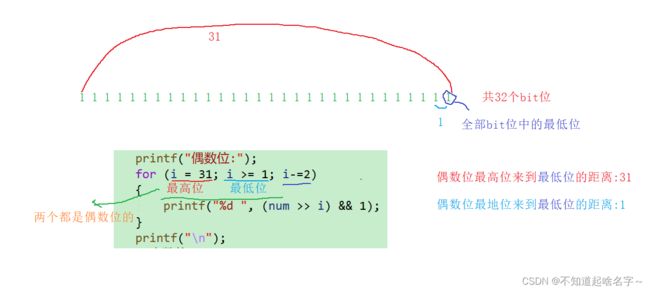
	//偶数位
	printf("偶数位:");
	for (i = 31; i >= 1; i-=2)
	{
		printf("%d ", (num >> i) && 1);
	}
	printf("\n");
	//奇数位
	printf("奇数位:");
	for (i = 30; i >= 0; i-=2)
	{
		printf("%d ", (num >> i) & 1);
	}
	printf("\n");
	return 0;
}

以偶数位为例子,图解:

执行效果: 

4.两个int(32位)整数m和n的二进制表达中,有多少个bit位不同?

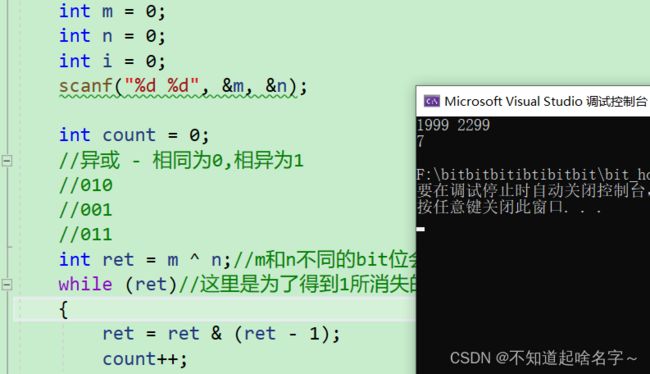
编程实现：两个int（32位）整数m和n的二进制表达中，有多少个位(bit)不同？ 

输入例子:

1999 2299

输出例子:7

方法1：m和n两者分别&1得到其二进制位最低位进行比较

int main()
{
	int m = 0;
	int n = 0;
	int i = 0;
	scanf("%d %d", &m, &n);

	int count = 0;
	for (i = 0; i < 32; i++)
	{
		if (((m >> i)&1)!= ((n >> i)&1))//这里不能把&1省略了
		{
			count++;
		}
	} 
	printf("%d\n", count);
	return 0;
}

把&1是否省略的区别在于: 

• 移位之后&1得到的是二进制序列里面的最低位,若没有&1,比较的时候是两个数字本身
• 相对的是有&1,是在比最低位,无,是比较所有位对应的数字

图解:

 像这样无论怎么移都count都不会++的，因为它们不是全部bit位对应相等

方法2：异或之后使用:n=n&(n-1)

#include
int main()
{
	int m = 0;
	int n = 0;
	int i = 0;
	scanf("%d %d", &m, &n);

	int count = 0;
	//异或 - 相同为0,相异为1
	//010
	//001
	//011
	int ret = m ^ n;//m和n不同的bit位会得到结果二进制的1
	while (ret)//这里是为了得到1所消失的次数,1消失了几次,就说明有几个1,而1又是区分不同bit位的标志
	{
		ret = ret & (ret - 1);
		count++;
	}
	printf("%d\n", count);
	return 0;
}

思想：如何判断一个数是不是 2 的幂次方?

2 的幂次方 的数：二进制中只有1个1
2 - 10
4 - 100
8 - 1000
 ...
n&(n-1) == 0

当&的结果为0,可以证明这个数就是2^n数

反例:

3

0011

0010--结果为0010,不是2^n数

算术转换

1.编译器导致结果差异

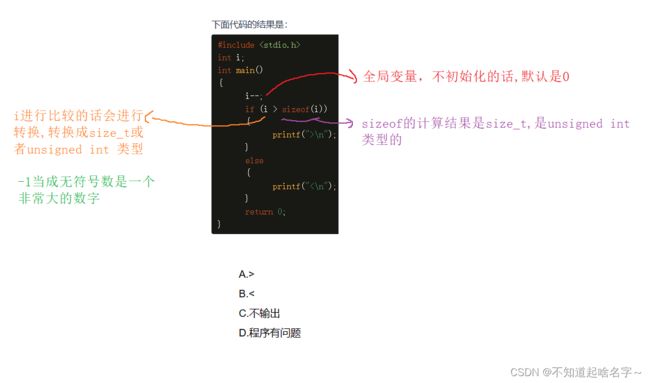
下面代码的结果是：10 or 12？

#include 
int main()
{
    int i = 1;
    int ret = (++i)+(++i)+(++i);
    printf("ret = %d\n", ret);
	return 0;
}

答:程序错误

原因:在vs环境底下是12,在gcc环境底下是10

2.sizeof的返回值类型

下面代码的结果是：

#include 
int i;
int main()
{
    i--;
    if (i > sizeof(i))
    {
        printf(">\n");
    }
    else
    {
        printf("<\n");
    }
    return 0; 
}

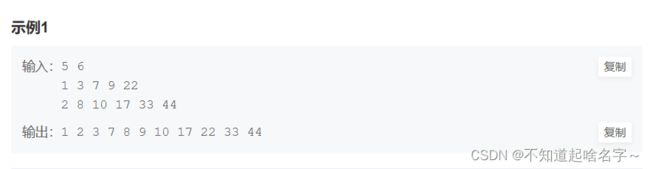
3.有序数列的合并

注意:是有序数组

#include
int main() {
    int n = 0;
    int m = 0;
    scanf("%d %d", &n, &m);
    int arr1[n];
    int arr2[m];
    int arr3[n + m];

    int i = 0;
    for (i = 0; i < n; i++) {
        scanf("%d", &arr1[i]);
    }
    for (i = 0; i < m; i++) {
        scanf("%d", &arr2[i]);
    }
    i = 0;
    int j = 0; //遍历arr2数组
    int k = 0; //放到第三个数组中去
    while (i < n && j < m) {
        if (arr1[i] < arr2[j]) {
            arr3[k] = arr1[i];
            i++;
            k++;
        } else {
            arr3[k] = arr2[j];
            j++;
            k++;
        }
    }
    if (i == n) {
        for (; j < m; j++) {
            arr3[k] = arr2[j];
            k++;
        }
    }
    if (j == m) {
        for (; i < n; i++) {
            arr3[k] = arr1[i];
            k++;
        }
    }
    for (k = 0; k < n + m; k++) {
        printf("%d ", arr3[k]);
    }
}

图解: 

 执行:

4.小乐乐走台阶

#include
int Upstairs(int n)
{
    if (n == 1)
        return  1;
    else if (n == 2)
        return   2;
    else
        return Upstairs(n - 1) + Upstairs(n - 2);
 
}
int main()
{
    int n;
    scanf("%d", &n);
    int ret=Upstairs(n);
    printf("%d", ret);
    return 0;
}

 跟青蛙跳台阶类似 

5.变种水仙花

#include 
#include
int main() {
    int i = 0;
    int n = 0;
    //sum定义的时候不能放在循环最外层循环外面，因为每次再回到j循环那sum没有得到重置,导致程序错误
    for (i = 10000; i < 99999; i++)
    {
        int j = 0;
        int sum = 0;
        for (j = 1; j <= 4; j++) {
            n = (int)pow(10, j);//pow函数返回的是double类型,所以需要强制转换成int
            sum = sum + (i / n) * (i % n);
        }
        if (sum == i)
        {
            printf("%d ", sum);
        }
    }

}

6.三角形的判断

#include 

int main() {
    int a = 0;
    int b = 0;
    int c = 0;
    while (scanf("%d %d %d", &a, &b, &c) == 3) {
        if (a + b > c && a + c > b && b + c > a)//这里先把判断三角形的条件写在最外层循环,那么在内层循环就不用都添加这个条件了
          {
            if (a == b && a == c && b == c)//等边
           {
                printf("Equilateral triangle!\n");
           }
           else if ((a == b && a != c) || (a == c && a != b) || (b == c && b != a))//等腰 
            {
                printf("Isosceles triangle!\n");
            }
            else//普通三角形
            {
                printf("Ordinary triangle!\n");
            }
        }
        else {
            printf("Not a triangle!\n");
        }
    }
    return 0;
}