算法套路八——二叉树深度优先遍历（前、中、后序遍历）

算法套路八——二叉树深度优先遍历（前、中、后序遍历）

算法示例：LeetCode98：验证二叉搜索树

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下：
节点的左子树只包含 小于 当前节点的数。
节点的右子树只包含 大于 当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。

方法一：前序遍历——先判断，再递归

前序遍历即先遍历根节点，再遍历左右子树
前序遍历我们的思路是先判断当前结点是否满足二叉搜索树的条件，再递归左右子树。

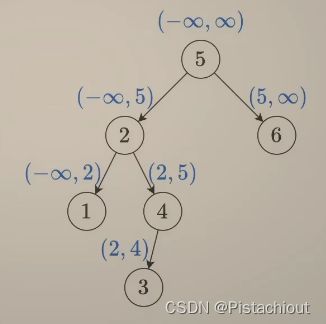
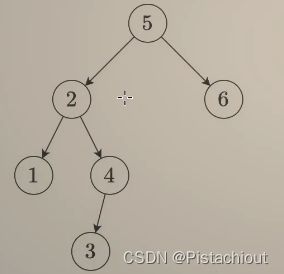
且如上图所示，在二叉搜索树中，使用前序遍历时有如上的规律，从根节点传递取值范围，对于任意一个结点，其取值范围已经确定，若结点值不在范围内，则不是二叉搜索树。
步骤如下所示：

1. root结点的取值范围为(-inf，+inf)，判断是否满足条件
2. 判断左子树是否是二叉搜索树，且此时最大值应该小于root.val，所以取值范围为（-inf，root.val]
3. 判断右子树是否是二叉搜索树，且此时最小值应该大于root.val，所以取值范围为[root.val,inf)
4. 对于2,3采取递归遍历

且注意判断root是否为空

class Solution:
    def isValidBST(self, root: Optional[TreeNode], left=-inf, right=inf) -> bool:
        if root is None:
            return True
        x = root.val
        return left < x < right and \
               self.isValidBST(root.left, left, x) and \
               self.isValidBST(root.right, x, right)

方法二：中序遍历——先判断，再递归

中序遍历即先遍历左节点、根节点，最后遍历右节点
且中序遍历下二叉搜索树应该为递增数组，所以我们直接判断当前节点值是否大于上一个遍历的节点值pre
其实这也等价于约束节点的范围，在中序遍历时只需要修改最小值，即取值范围是(pre,inf)

1. 判断左子树是否是二叉搜索树，且记录左子树最后一个被遍历的节点值为pre，也是左子树的最大值
2. 比较当前节点指是否大于pre，即取值范围是(pre,inf)，
3. 判断右子树是否是二叉搜索树
4. 对于1,3采取递归遍历

class Solution:
    pre = -inf
    def isValidBST(self, root: Optional[TreeNode]) -> bool:
        if root is None:
            return True
        if not self.isValidBST(root.left):
            return False
        if root.val<=self.pre:
            return False
        self.pre = root.val
        return self.isValidBST(root.right)
        

方法三：后序遍历——先递归，在判断

后序遍历即先遍历左节点、右节点，最后遍历根节点
后序遍历也可以传递节点的范围，不过是从叶子节点向根节点传递，根节点需要大于左子树的最大值，小于右子树的最小值。

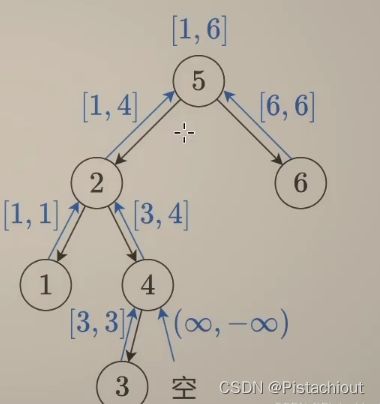
1. 如果当今节点为null空节点，则返回(inf,-inf)，因为任何值都会小于inf，任何值都会大于-inf，这样就不会影响到树的最大最小值的取值，可以仔细体会。
2. 遍历左子树，且返回左子树的最小值l_min与最大值l_max
3. 遍历右子树，且返回右子树的最小值r_min与最大值r_max
4. 比较当前节点的值，若取值位于（l_max ,r_min)，则更新最小值与最大值并返回即min(l_min, x), max(r_max, x)。若取值不在范围内，则表示不是二叉搜索树，此时我们返回正常情况不会返回的（-inf，inf）来表示False
5. 比较返回值是否是正常值，这等价与判断是否等于inf无穷即非正常值，若等于inf则返回False，若不等于inf则返回True

class Solution:
    def isValidBST(self, root: Optional[TreeNode]) -> bool:
        def dfs(node: Optional[TreeNode]) -> Tuple:
            if node is None:
                return inf, -inf
            l_min, l_max = dfs(node.left)
            r_min, r_max = dfs(node.right)
            x = node.val
            # 也可以在递归完左子树之后立刻判断，如果不是二叉搜索树，就不用递归右子树了
            if x <= l_max or x >= r_min:
                return -inf, inf#返回无穷表示为False，不满足搜索树
            return min(l_min, x), max(r_max, x)
        return dfs(root)[1] != inf

总结：

前序遍历在某些数据下不需要递归到边界（base case）就能返回，而另外两种需要递归到至少一个边界，从这个角度上来说它是最快的。
中序遍历很好地利用到了二叉搜索树的性质，使用到的变量最少。
后序遍历的思想是最通用的，即自底向上计算子问题的过程。想要学好动态规划的话，请务必掌握这个思想。
且由以上示例代码都可以看出，在代码书写时要定义内部匿名函数dfs，不然可能会由于LeetCode判断问题影响结果

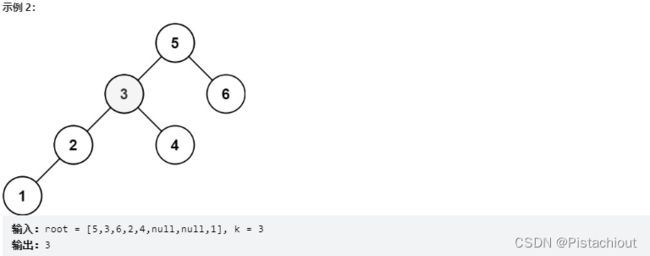
算法练习一：LeetCode230. 二叉搜索树中第K小的元素

给定一个二叉搜索树的根节点 root ，和一个整数 k ，请你设计一个算法查找其中第 k 个最小元素（从 1 开始计数）。

利用特性中序遍历下二叉搜索树应该为递增数组
本题可以采用中序遍历，每次遍历时k–，当k为0时则表示当前结点为第k个结点，则令ans等于该值

func kthSmallest(root *TreeNode, k int) int {
    var ans int
    var dfs func(node *TreeNode) 
    dfs=func(node *TreeNode) {
        if node==nil{
            return 
        }
        dfs(node.Left)
        k--
        if k==0{
            ans=node.Val
        }
        dfs(node.Right)
    }
    dfs(root)
    return ans
}

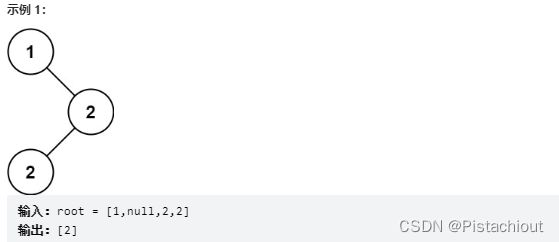
算法练习二：LeetCode501. 二叉搜索树中的众数

给你一个含重复值的二叉搜索树（BST）的根节点 root ，找出并返回 BST 中的所有 众数（即，出现频率最高的元素）。如果树中有不止一个众数，可以按 任意顺序 返回。

利用特性中序遍历下二叉搜索树应该为递增数组
本题可以采用中序遍历，将遍历节点与前一个节点比较，然后使用变量cur，max来记录当前节点与最多节点，且注意要定义匿名函数解决。

func findMode(root *TreeNode) []int {
    var (
        ans []int
        pre, cur, max int
        dfs func(*TreeNode)
    )
    dfs = func(node *TreeNode) {
        if node == nil {
            return
        }
        dfs(node.Left)
        if node.Val == pre {
            cur++
        } else {
            cur = 1
        }
        if cur > max {
            max = cur
            ans = []int{node.Val}
        } else if cur == max {
            ans = append(ans, node.Val)
        }
        pre = node.Val
        dfs(node.Right)
    }
    dfs(root)
    return ans
}

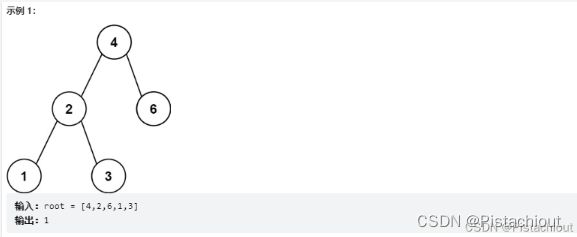
算法练习三：LeetCode530. 二叉搜索树的最小绝对差

给你一个二叉搜索树的根节点 root ，返回 树中任意两不同节点值之间的最小差值 。差值是一个正数，其数值等于两值之差的绝对值。

利用特性中序遍历下二叉搜索树应该为递增数组
本题可以采用中序遍历，将遍历节点与前一个节点比较，然后使用变量pre，min来记录前一个结点节点值与当前最小差值，并定义匿名函数解决。

func getMinimumDifference(root *TreeNode) int {
    min, pre := math.MaxInt64, -1
    var dfs func(node *TreeNode)
    dfs=func(node *TreeNode){
    if node==nil{
        return 
    }
    dfs(node.Left)
    sub:=node.Val-pre
    if sub<min&&pre!=-1{
        min=sub
    }
    pre=node.Val
    dfs(node.Right)
}
    dfs(root)
    return min
}

算法练习四：LeetCode700. 二叉搜索树中的搜索

给定二叉搜索树（BST）的根节点 root 和一个整数值 val。你需要在 BST 中找到节点值等于 val 的节点。 返回以该节点为根的子树。 如果节点不存在，则返回 null。

若 root 为空则返回空节点；
若 val=root.val，则返回 \textit{root}root；
若val 若 val>root.val，递归右子树。

func searchBST(root *TreeNode, val int) *TreeNode {
    if root == nil {
        return nil
    }
    if val == root.Val {
        return root
    }
    if val < root.Val {
        return searchBST(root.Left, val)
    }
    return searchBST(root.Right, val)
}

算法进阶一：LeetCode236. 二叉树的最近公共祖先

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

本题可以使用分类讨论，如下图所示，定义函数dfs()返回当前结点node的子树是否找到p或q，有以下情况

func lowestCommonAncestor(root, p, q *TreeNode) *TreeNode {
	return dfs(root,p,q)
}
func dfs(node, p, q *TreeNode) *TreeNode{
    if node == nil || node == p || node == q {
		return node
	}
	left := dfs(node.Left, p, q)
	right := dfs(node.Right, p, q)
	if left != nil && right != nil {
		return node
	}
	if left != nil {
		return left
	}
	return right
}

算法进阶二：LeetCode236. 二叉树的最近公共祖先

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

本题与上题一样，只不过在判断p，q的位置时可以利用线索二叉树值的大小性质来判断

func lowestCommonAncestor(root, p, q *TreeNode) *TreeNode {
	return dfs(root,p,q)
}
func dfs(node, p, q *TreeNode) *TreeNode{
    if node == nil || node == p || node == q {
		return node
	}
	if node.Val>p.Val&&node.Val>q.Val{
        return dfs(node.Left,p,q)
    }else if node.Val<p.Val&&node.Val<q.Val{
        return dfs(node.Right,p,q)
    }
    return node
}