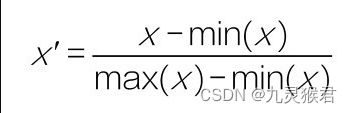使用线性回归预测网店的销售额
使用线性回归预测网店的销售额
描述
一个店的基本情况是这样的：正式运营一年多，流量、订单数和销售额都显著增长。经过一段时间的观察，发现网店商品的销量和广告推广的力度息息相关。店家在微信公众号推广，也通过微博推广，还在一些其他网站上面投放广告。当然，投入推广的资金越多，则商品总销售额越多。店家想：“能不能通过机器学习算法，根据过去记录下来的广告投放金额和商品销售额，来预测在未来的某个节点，一个特定的广告投放金额对应能实现的商品销售额？” ，我们使用线性回归模型实现网店销售额的预测。
本任务主要实践内容包括：
1、 关于网店销售额回归问题的定义
2、 数据的收集、分析和预处理
3、如何建立机器学习模型
4、 如何通过梯度下降找到最佳参数
5、线性回归模型的实现
- 一元（单变量）线性回归模型
- 多元（多变量）线性回归模型
源码下载
环境
-
操作系统：Windows10、Ubuntu18.04
-
工具软件：Anaconda3 2019、Python3.7
-
硬件环境：无特殊要求
-
依赖库列表
scikit-learn 0.24.2
分析
1、机器学习实战的整体流程
- 明确定义所要解决的问题—网店销售额的预测。
- 在数据的收集和预处理环节，分5个环节完成数据的预处理工作，分别如下。
- 收集数据：需要店家网店的相关记录
- 将收集到的数据可视化，显示出来看一下
- 做特征工程，使数据更容易被机器处理
- 拆分数据集为训练集和测试集
- 做特征缩放，把数据值压缩到比较小的区间
- 选择机器学习模型：构建模型
- 确定机器学习的算法—这里也就是线性回归算法。
- 模型训练
- 模型评估
2、数据介绍
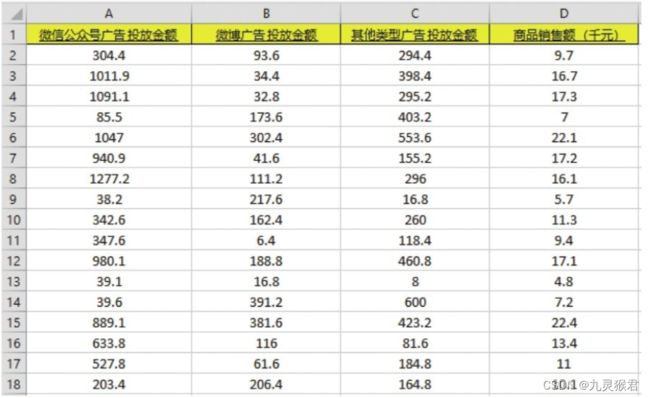
已经把故去每周的广告投放金额和销售数据整理成一个Excel表格，并保存为advertising.csv文件（这是以逗号为分隔符的一种文件格式，比较容易被python读取）。基本上每周的各种广告投放金额和商品销售额都记录在案。
这个重要的数据记录是实现本实验的机器学习项目的基础。
- 微信公众号广告投放金额（下文中用"微信"代指）、微博广告投放金额（下文中用“微博”代指）、其他类型广告投放金额（下文用“其他”代指），这3个字段是特征（也是开店的人可以调整的）。
- 商品销售额（下文用"销售额"代指）是标签（也是开店的人希望去预测的）。
每一个类型广告的广告投放金额都是一个特征，因此这个数据集中含有3个特征。也就是说，它是一个多元回归问题。
3、拆分数据集为训练集和测试集
在开始建模之前，还需要把数据集拆分为两个部分：训练集和测试集。在普通的机器学习项目中，至少要包含这两个数据集，一个用于训练机器，确定模型，另一个用于测试模型的准确性。不仅如此，往往还需要一个验证集，以在最终测试之前增加验证环节。目前这个问题比较简单，数据量也少，我们简化了流程，合并了验证和测试环节。
这两个数据集需要随机分配，两者间不可以出现明显的差异性。因此，在拆分之前，要注意数据是否已经被排序或者分类，如果是，还要先进行打乱。
使用下面的代码段将数据集进行80%（训练集）和20%（测试集）的分割：
# 将数据集进行80%（训练集）和20%（验证集）的分割
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(特征数据x, 标签数据y,
test_size=0.2, random_state=0)
- Sklearn中的train_test_split函数，是机器学习中拆分数据集的常用工具。
- test_size=0.2，表示拆分出来的测试集占总样本量的20%。
- 如果用print语句输出拆分之后的新数据集（如X_train、X_test）的内容，会发现这个工具已经为数据集进行了乱序（重新随机排序）的工作，因为其中的shuffle参数默认值为True。
- 而其中的random_state参数，则用于数据集拆分过程的随机化设定。如果指定了一个整数，那么这个数叫作随机化种子，每次设定固定的种子能够保证得到同样的训练集和测试集，否则进行随机分割。
4、数据归一化
特征缩放的常用方法，包括标准化、数据的压缩（也叫归一化），以及规范化等。特征缩放对于机器学习特别重要，可以让机器在读取数据的时候感觉更“舒服”，训练起来效率更高。
这里就对数据进行归一化。归一化是按比例的线性缩放。数据归一化之后，数据分布不变，但是都落入一个小的特定区间，比如0～1或者-1～+1，如右图所示。
常见的一个归一化公式如下：
通过Sklearn库中preprocessing（数据预处理）工具中的MinMaxScaler可以实现数据的归一化。核心代码如下：
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
# 对特征归一化
result = scaler.fit_transform(待归一化数据)
5、线性回归模型
对于这个案例，虽然上图中的函数直线并未精确无误地穿过每个点，但已经能够反映出特征（也就是微信公众号广告投放金额）和标签（也就是商品销售额）之间的关系，拟合程度还是挺不错的。
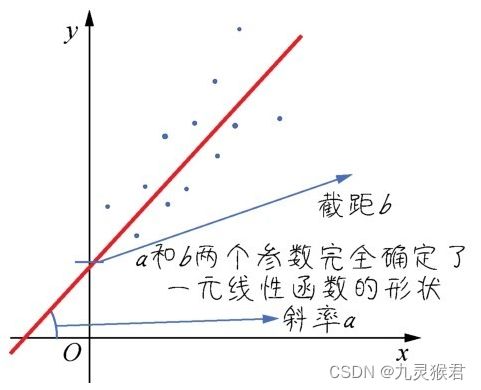
这个简单的模型就是一元线性函数（如下图所示）：
- 其中，参数a的数学含义是直线的斜率（陡峭程度），b则是截距（与y轴相交的位置）。
- 在机器学习中，会稍微修改一下参数的代码，把模型表述为：
y=wx+b
此处，方程式中的a变成了w，在机器学习中，这个参数代表权重（weight）。因为多元变量（多特征）的情况下，一个特征对应的w参数越大，就表示权重越大。而参数b，在机器学习中称为偏置(bias)。
这个简单的线性函数，在后续机器学习过程中，会作为一个基本运算单元反复的发挥威力。
实施
1、问题定义
我们定义的问题都与广告投放金额和商品销售金额有关，我们希望通过机器学习算法找出答案。
（1） 各种广告和商品销售额的相关度如何？
（2）各种广告和商品销售额之间体现出一种什么关系？
（3） 哪一种广告对商品销售额的影响最大？
（4）分配特定的广告投放额。，预测出未来的商品销售额。
以上是我们定义的问题，广告投放金额和商品销售额之间，明显呈现一种相关性，
机器学习算法正是通过分析已有的数据，发现两者之间的关系，也就是发现一个能由“此”推知“彼”的函数。本课通过回归分析来寻找这个函数。所谓回归分析（regression analysis），是确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法，也就是研究当自变量变化时，因变量以何种形式在变化。在机器学习领域，回归应用于被预测对象具有连续值特征的情况（如客流量、降雨量、销售量等），所以用它来解决这几个问题非常合适。
2、数据收集和预处理
网店销售数据参考advertising.csv,详细介绍参考数据介绍部分。
2.1 数据读取和可视化
新建1-数据读取和可视化.ipynb文件，通过下面的代码把数据读入Python运行环境，并运行代码：
# 示例代码中或有不当之处，欢迎读者提出改进，作者邮箱[email protected]
import numpy as np # 导入NumPy数学工具箱
import pandas as pd # 导入Pandas数据处理工具箱
# 读入数据并显示前面几行的内容，这是为了确保我们的文件读入的正确性
# 读入文件，如果在本机中需要指定具体本地路径
df_ads = pd.read_csv('../dataset/advertising.csv')
df_ads.head()
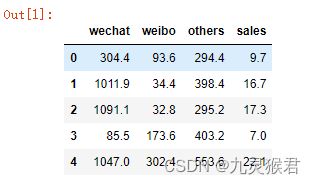
这里的变量命名为df_ads，df代表这是一个Pandas Dataframe格式数据，ads是广告的缩写。输出结果（如下图所示）显示数据已经成功地读入了Dataframe。
显示前5行数据
2.2 数据的相关分析
然后对数据进行相关分析（correlation analysis）。相关分析后我们可以通过相关性系数了解数据集中任意一对变量（a,b) 之间的相关性。相关性系数是一个-1~1的值，正值表示相关，负值表示负相关。数值越大，相关性越强，如果a和b的相关系数是1，则a和b总是相等的。如果a和b的相关性系数是0.9 ，则b会显著地随着a的变化而变化，而且变化的趋势保持一致。如果a和b的相关性系数是0.3，则说明两者并没有什么明显的联系。
在Python中，相关分析用几行代码即可实现，并可以用热力图（heatmap）的方式非常直观地展示出来：
#导入数据可视化所需要的库
import matplotlib.pyplot as plt #Matplotlib – Python画图工具库
import seaborn as sns #Seaborn – 统计学数据可视化工具库
# 对所有的标签和特征两两显示其相关性热力图(heatmap)
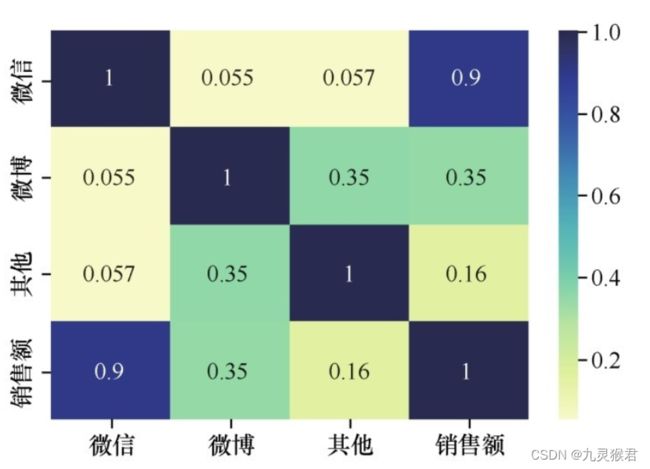
sns.heatmap(df_ads.corr(), cmap="YlGnBu", annot = True)
plt.show() # plt代表英文plot,就是画图的意思
运行结果：
运行代码之后，3个特征加一个标签共4组变量之间的相关性系数全部以矩阵形式显示，而且相关性越高，对应的颜色越深。此处相关性分析结果很明确地向我们显示—将有限的金钱投放到微信公众号里面做广告是最为合理的选择。
看起来其他两种广告的投放对网店销售额的影响甚微啊。
2.3 数据的散点图
下面，通过散点图（scatter plot）两两一组显示商品销售额和各种广告投放金额之间的对应关系，来将重点聚焦。散点图是回归分析中，数据点在直角坐标系平面上的分布图，它是相当有效的数据可视化工具。
# 显示销量和各种广告投放量的散点图
sns.pairplot(df_ads, x_vars=['wechat', 'weibo', 'others'],
y_vars='sales',
height=4, aspect=1, kind='scatter')
plt.show()
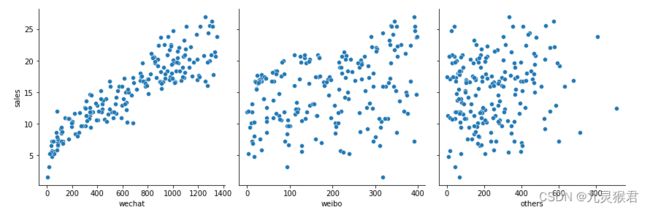
输出结果如下图所示：
代码运行之后输出的散点图清晰地展示出了销售额随各种广告投放金额而变化的大致趋势，根据这个信息，就可以选择合适的函数对数据点进行拟合。
2.4 数据集清洗和规范化
通过观察相关性和散点图，发现在本例的3个特征中，微信广告投放金额和商品销售额的相关性比较高。因此，为了简化模型，我们将暂时忽略微博广告和其他类型广告投放金额这两组特征，只留下微信广告投放金额数据。这样，就把多变量的回归分析简化为单变量的回归分析。
下面的代码把df_ads中的微信公众号广告投放金额字段读入一个NumPy数组,，也就是清洗了其他两个特征字段，并把标签读入数组y:
X = np.array(df_ads.wechat) #构建特征集，只有微信广告一个特征
y = np.array(df_ads.sales) #构建标签集，销售金额
print ("张量X的阶:",X.ndim)
print ("张量X的形状:", X.shape)
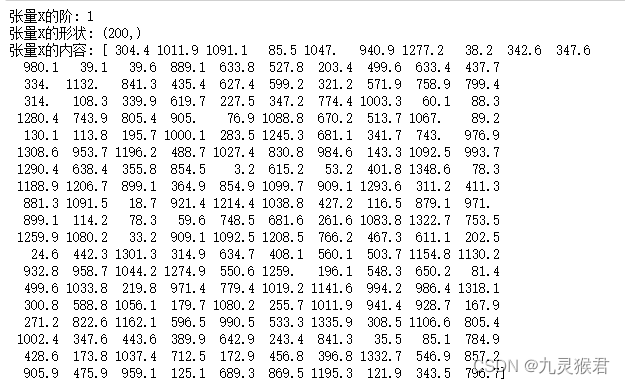
print ("张量X的内容:", X)
输出如下，结果显示特征集,是阶为1的1D张量，这个张量总共包含200个样本，都是每周的微信广告投放金额数据。
（200，）这种表述形式代表一个有200个样本数据为1阶的张量数组，也就是一个向量。目前数组中只有一个特征，张量的阶为1，那么这个1D的特征张量，是机器学习算法能够接受的格式吗？
对于回归问题的数值类型数据集，机器学习模型所读入的规范格式应该是2D张量，也就是矩阵，其形状为（样本数，标签数）.其中的行是数据，而其中的列是特征。大家可以把它想象成Excel表格的格式。那么就现在的特征张量X而言，则要把它的形状从(200,) 变成(200,1),然后再进行机器学习，因此需要用reshape方法给上面的张量变形，代码如下：
# X = X.reshape((len(X),1)) #通过reshape函数把向量转换为矩阵，len函数返回样本个数
# y = y.reshape((len(y),1)) #通过reshape函数把向量转换为矩阵，len函数返回样本个数
X = X.reshape(-1,1) #通过reshape函数把向量转换为矩阵，len函数返回样本个数
y = y.reshape(-1,1) #通过reshape函数把向量转换为矩阵，len函数返回样本个数
print ("张量X的阶:",X.ndim)
print ("张量X的形状:", X.shape)
输出结果:
张量X的阶: 2
张量X的形状: (200, 1)
此时的张量升阶了，变成一个2D矩阵，每一个数据样本就占据矩阵的一行：
张量X的阶: 2
张量X的维度: (200, 1)
张量X的内容:
现在数据格式从（200，）变成了（200，1）。尽管还是200个数字，但是数据的结构从一个1D数组变成了有行。再次强调，对于常见的连续性数值数据集（也叫向量数据集），输入特征集是2D矩阵，包含两个轴。有列的矩阵
2.5 拆分数据集为训练集和测试集
使用下面的代码段将数据集进行80%（训练集）和20%（测试集）的分割：
# 将数据集进行80%（训练集）和20%（验证集）的分割
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y,
test_size=0.2, random_state=0)
2.6 把数据归一化
通过Sklearn库中preprocessing（数据预处理）工具中的MinMaxScaler可以实现数据的归一化。
# 调用sklearn自动实现归一化
from sklearn.preprocessing import MinMaxScaler
scaler = MinMaxScaler()
# 对特征归一化
X_train,X_test = scaler.fit_transform(X_train),scaler.fit_transform(X_test)
# 对标签归一化
y_train,y_test = scaler.fit_transform(y_train),scaler.fit_transform(y_test)
#print('自动归一化结果:',X_train)
输出结果:
自动归一化结果:
[[0.39995488]
[0.72629521]
[0.22746071]
[0.66952402]
[0.81803143]
[0.35341003]
[0.24355215]
[0.44852996]
[0.44544703]
[0.71636965]
[0.46597489]
[0.46319272]
[0.11594857]
[0.07353936]
[0.97706594]
[0.45770359]
[0.22204677]
[0.1898639 ]
...
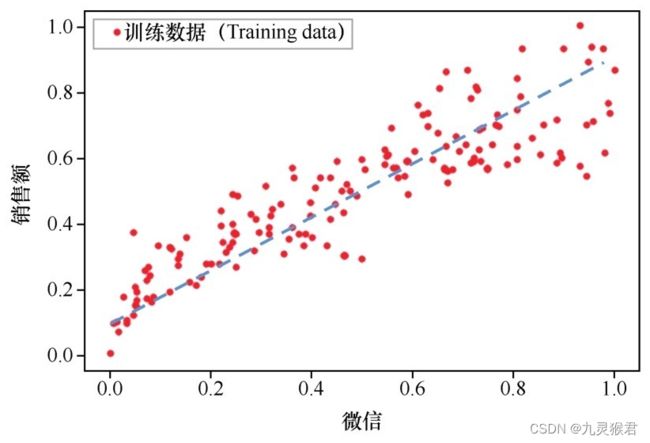
下面代码是显示数据被压缩处理之后的散点图，形状和之前的图完全一致，只是数值已被限制在一个较小的区间：
#用之前已经导入的matplotlib.pyplot中的plot方法显示散点图
plt.plot(X_train,y_train,'r.', label='Training data')
plt.xlabel('Wechat Ads') # x轴Label
plt.ylabel('Sales') # y轴Label
plt.legend() # 显示图例
plt.show() # 显示绘图结果
手工画一条x和y之间的线性回归直线（数值已经归一化从两三百压缩到比较小的值）。
目前的数据准备、分析、包括简单的特征工程工作已经全部完成，下面进入机器学习建模与训练机器学习的关键环节。
3、模型构建和训练
3.1 确定线性回归模型
构建线性回归模型的接口为LinearRegression() 包含在sklearn.linear_model模块中，创建线性回归模型，可以直接使用fit()接口对模型进行训练。
3.2 构建模型
使用``LinearRegression()` 接口创建线性回归模型
from sklearn.linear_model import LinearRegression #导入线性回归算法模型
model = LinearRegression() #使用线性回归算法
3.3 模型训练
使用fit()接口对模型进行训练，接口参数为训练集特征X_train和测试集标签y_train：
# 模型训练
model.fit(X_train, y_train) #用训练集数据，训练机器，拟合函数，确定参数
4、模型评估和预测
通过模型的score()接口对模型进行准确率的计算，接口参数为测试集特征X_test和测试集真实标签
y_test。
# 模型评估
y_pred = model.predict(X_test) #预测测试集的Y值
print ('销量的真值(测试集)',y_test)
print ('预测的销量(测试集)',y_pred)
print("线性回归预测评分：", model.score(X_test, y_test)) #评估预测结果
输出结果：
销量的真值(测试集) [[ 0.37815126]
[ 0.90336134]
[ 0.73529412]
[ 0.71428571]
[ 0.14285714]
[ 0.76890756]
[ 0.58823529]
[ 0.79831933]
[ 0.16806723]
[ 0.63865546]
[ 0.74369748]
[ 0.31092437]
[ 0.45378151]
[ 0.65966387]
[ 0.88235294]
[ 0.10504202]
[ 0.42016807]
[ 0.81512605]
[ 0.71008403]
[-0.06722689]
[ 0.51680672]
[ 0.56302521]
[ 0.73529412]
[ 0.31932773]
[ 0.96638655]
[ 0.34033613]
[ 0.55462185]
[ 0.31512605]
[ 0.74369748]
[ 0.23109244]
[ 0.28991597]
[ 0.7394958 ]
[ 0.39495798]
[ 0.60084034]
[ 0.73529412]
[ 0.70168067]
[ 0.71428571]
[ 0.79411765]
[ 0.36554622]
[ 0.36134454]]
预测的销量(测试集) [[0.47947693]
[0.66283604]
[0.70328437]
[0.60156726]
[0.18237553]
[0.68022783]
[0.63227619]
[0.73200566]
[0.18441286]
[0.68952001]
[0.63863661]
[0.36752352]
[0.37771013]
[0.7014955 ]
[0.75550942]
[0.18371719]
[0.47266929]
[0.62825123]
[0.66328326]
[0.1663254 ]
[0.51878236]
[0.6711841 ]
[0.70576891]
[0.24816617]
[0.81498932]
[0.32121168]
[0.55475852]
[0.39172294]
[0.81136189]
[0.20294753]
[0.26580641]
[0.78353504]
[0.31420527]
[0.7014955 ]
[0.58278414]
[0.59068498]
[0.72634091]
[0.68499815]
[0.34605708]
[0.29472647]]
线性回归预测评分： 0.8493759729652093
观察结果可以发现，我们预测值和真实值是非常接近的，评分达到84%，此模型可用。
使用线性岭回归算法模型预测
from sklearn.linear_model import Ridge #导入线性岭回归算法模型
model = Ridge() #使用线性回归算法
model.fit(X_train, y_train) #用训练集数据，训练机器，拟合函数，确定参数
y_pred = model.predict(X_test) #预测测试集的Y值
print("线性回归预测评分：", model.score(X_test, y_test)) #评估预测结果
输出结果：
线性回归预测评分： 0.832199701556618
Ridge 和 LinearRegression 模型预测结果基本一致。
5、实现多元线性回归
多元，既多变量，也就是特征多维的。我们原始数据本来就具有3个特征模型。只是为了简化教学，才只选择了微信公众号广告投放金额作为唯一的特征，构建单变量线性回归模型。
读取数据
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import MinMaxScaler
df_ads = pd.read_csv('advertising.csv')
X = np.array(df_ads)# 这次在构建特征数据时，保留所有字段，包括wechat,weibo,others
X =np.delete(X,[3],axis=1) # 删除标签
y=np.array(df_ads.sales) # 构建标签集，销售额
print('张量X的阶:',X.ndim)
print('张量X的维度:',X.shape)
输出结果为张量的基本信息，能发现是二维矩阵，包含200行，3个列。
张量X的阶: 2
张量X的维度: (200, 3)
数据集拆分和预处理
X_train, X_test, y_train, y_test = train_test_split(X, y,
test_size=0.2, random_state=0) # 拆分数据集
X_train = scaler.fit_transform(X_train) # 训练集特征归一化
X_test = scaler.fit_transform(X_test) # 测试特征归一化
构建多元线性回归
lr = LinearRegression() # 线性回归
lr.fit(X_train,y_train) # fit 就相当于梯度下降
score = lr.score(X_test,y_test)
print("Sklearn线性回归准确率:{:.2f}%".format(score*100))
输出结果为模型预测准确率：
Sklearn线性回归准确率:85.86%
预测
在问题定义时，我们提出：在未来的某周，当我们将各种广告投放金额做一个分配（比如：我决定用250元，50元，50元）来进行一周的广告投放时，我将大概实现多少元的商品销售额？
X_plan=[[250,50,50]] # 要预测的X特征值
X_plan=scaler.transform(X_plan) # 对预测数据也要归一化缩放
pred = lr.predict(X_plan)
print(pred[0],"千元")
预测网店销售额为：
8.48645854453084 千元
通过上面的机器学习模型，可以计算出预计商品销售额为8千元。
多元线性回归**
lr = LinearRegression() # 线性回归
lr.fit(X_train,y_train) # fit 就相当于梯度下降
score = lr.score(X_test,y_test)
print("Sklearn线性回归准确率:{:.2f}%".format(score*100))
输出结果为模型预测准确率：
Sklearn线性回归准确率:85.86%
预测
在问题定义时，我们提出：在未来的某周，当我们将各种广告投放金额做一个分配（比如：我决定用250元，50元，50元）来进行一周的广告投放时，我将大概实现多少元的商品销售额？
X_plan=[[250,50,50]] # 要预测的X特征值
X_plan=scaler.transform(X_plan) # 对预测数据也要归一化缩放
pred = lr.predict(X_plan)
print(pred[0],"千元")
预测网店销售额为：
8.48645854453084 千元
通过上面的机器学习模型，可以计算出预计商品销售额为8千元。