贪心算法详解
前言
贪心算法是动态规划的一种特殊情况,需要满足更为苛刻的条件:贪心选择。
| 算法种类 | 时间复杂度 |
|---|---|
| 暴力算法 | 指数级别 |
| 动态规划 | 多项式级别 |
| 贪心算法 | 线性级别 |
什么是贪心选择性质呢,简单说就是:每一步都做出一个局部最优的选择,最终的结果就是全局最优。注意哦,这是一种特殊性质,其实只有一部分问题拥有这个性质。动态规划可以认为是含有重叠子问题的暴力算法,本质还是要穷举所有解空间,而贪心的精髓在于不用穷举所有解空间,就能找到答案。所以准确说应该是,能够用贪心算法解决的问题,一定能用暴力穷举的方式求解。当然,几乎所有计算机算法问题,都能用暴力穷举的方式求解。
上面虽然说明,一定情况下,贪心算法能够比动态规划达到更好的时间复杂度,但是并不意味着贪心算法比动态规划算法简单,举两个分别应用两个算法的例子:
1、给你一叠纸币,你可以取10张,问怎样能使得取出的钱最多?
2、给你一个箱子体积为N,你有一堆货物,如何尽可能把箱子装满?
上面两个问题分别对应贪心算法与动态规划,第2题使用贪心算法是无法解决的,因为有箱子体积的限制。
下面选则几道比较难的题目体会贪心与动态规划解题的解题。
1、摆动序列

首先看到题目是最值问题,最终的要求是求最长子序列的长度,所以第一个念头是想到动态规划的,恰好我们有一道现成的题目,最长递增子序列,是不是可以借鉴呢?反正我想不到,哈哈哈
class Solution {
public int wiggleMaxLength(int[] nums) {
if(nums.length==1)
{
return nums.length;
}
int n=nums.length;
int prediff=0;
int curdiff=0;
int result=1;
for(int i=0;i<n-1;i++)
{
curdiff=nums[i+1]-nums[i];
if((curdiff>0 && prediff<=0)|| (curdiff<0 && prediff>=0))
{
result++;
prediff=curdiff;
}
}
return result;
}
}
关于代码中,我在编写的时候出过这样的问题
问题1:
为什么prediff=curdiff; 写在if判断条件之外会导致答案错误?
举一个反例,2,6,6,5,5,4,因为写在里面规避了除去端点之外的prediff=0情况的出现,换句话说,我们并不想判断prediff=0的情况,只是由于要判断起始点与终止点的情况。
还有一个特殊的反例[3,3,3,2,5],这个反例可以很好的证明为什么prediff=0一定要写在循环里面,而不能在开始循环之前进行或者在循环结束之后按特殊条件处理到prediff=0的情况,因为我们不知道真正进入比较的点在那个地方,在这个反例中是在index=2的位置。
问题2:
为什么result初始化为1?
这个可以分几种情况来讨论:
第一:如果只有1个数,按照题目的意思,直接返回1是正确的。
第二:如果有多个数 ,这个下面也可以分为几种情况
1:前两个数一样的情况,进入循环后,没有触发正确的判断机制,没有进入判断,故这时候到下一次循环,result依然应该为1
2:前两个数不一样,正常进入触发,两个数进行一次判断,但是有两个值,所以判断正确进入循环后,result++应该为2
这道题当然还有被称作动态规划的方法去做,其实不应该在贪心算法的范畴里面,但是这道题对于下面的分发糖果(两次贪心起到了很好的启发作用)。
我们可以设置一个上身子序列与下降子序列
class Solution {
public int wiggleMaxLength(int[] nums) {
int up=1;
int down=1;
int n=nums.length;
for(int i=1;i<n;i++)
{
if(nums[i-1]<nums[i])
{
up=down+1;
}
else if(nums[i-1]>nums[i])
{
down=up+1;
}
}
return Math.max(down,up);
}
}
2、跳跃游戏
这道题相对来说是有难度的,很难想到这样去做,因为这道题要涉及到一个覆盖范围的问题,我们要维护一个叫覆盖范围的东西,用一个变量去表示它,最终其能不能达到最后一个下标范围。
这道题的重点在于如何把下标与value值,结合起来,可以有多种结合的方式,本题选择了相加的方式。
k=Math.max(k,i+nums[i]);
class Solution {
public boolean canJump(int[] nums) {
//覆盖范围
int k=0;
int n=nums.length;
for(int i=0;i<n;i++)
{
if(i>k)
{
return false;
}
k=Math.max(k,i+nums[i]);
}
return true;
}
}
3、跳跃游戏II

这道题的思路其实可以不完善的想到一个,但是不敢用,就是让当前的可跳跃步数直接走到最大,但是我们怕漏了中间的大的跳跃数
比如说:3,0,4,1,1,1,3,这时候如果在i=0的时候直接走3步达到i=2时的nums[i]=1,错过了大跳跃数4,这个顾虑和上面一题的顾虑时一样的,还是需要依次遍历,获取覆盖最大值,重点在于不能更改遍历值,不能让自带逻辑修改i。
class Solution {
public int jump(int[] nums) {
int curdist=0;//当前跳跃值所能达到的最远下标
int nextdist=0;//下一次覆盖范围所能达到的最远下标
int ans=0;
for(int i=0;i<nums.length;i++)
{
nextdist=Math.max(nextdist,i+nums[i]);
if(i==curdist)//到达了当前所能到达的最远下标,依然在循环内
{
if(curdist!=nums.length-1)
{
curdist=nextdist;
ans++;
if(curdist>=nums.length-1)
{
break;
}
}
else
{
break;
}
}
}
return ans;
}
}
注意,由于我们初始条件下设置的curdist与nextdist都等于0,故我们要让循环运行起来,必须要让第一波i=curdist=0进入循环中,故题目中有三个个比较重要的位置,其顺序很重要
nextdist=Math.max(nextdist,i+nums[i]);
...
ans++;
if(curdist>=nums.length-1)
{
break;
}
这道题的第二种方式,将重复的逻辑合并到一起,当循环下标到达curdist之后,就直接步数+1
class Solution {
public int jump(int[] nums) {
int curdist=0;//当前跳跃值所能达到的最远下标
int nextdist=0;//下一次覆盖范围所能达到的最远下标
int ans=0;
for(int i=0;i<nums.length-1;i++)
{
nextdist=Math.max(nextdist,i+nums[i]);
if(i==curdist)//到达了当前所能到达的最远下标,依然在循环内
{
ans++;
curdist=nextdist;
}
}
return ans;
}
}
4、分发糖果
class Solution {
public int candy(int[] ratings) {
//分为两次贪心,如果想在一次贪心中解决左右两边的问题,会做不出来
int n=ratings.length;
int [] count=new int[n];
Arrays.fill(count,1);
//右边的孩子评分高的比左边的孩子多一个糖果
for(int i=1;i<n;i++)
{
if(ratings[i-1]<ratings[i])
{
count[i]=count[i-1]+1;
}
}
//左边的孩子评分高的比右边的孩子多一个糖果
for(int i=n-2;i>=0;i--)
{
if(ratings[i]>ratings[i+1])
{
count[i]=Math.max(count[i],count[i+1]+1);
}
}
int ret=0;
for(int i=0;i<n;i++)
{
ret+=count[i];
}
return ret;
}
}
我们关注的重点应该是左边的表现大于右边的表现得情况,这个情况下,不能直接的使用count[i]=count[i+1]+1。
因为啊,在次数未知的递增之后,如果出现一次下降,该小孩的糖果值是直接被设置为1的。举下面一个例子:
ratings评分表数组为:[1,2,3,1]
我们可以直接看出相应的每个孩子的糖果数应该为:[1,2,3,1]
但是如果count[i]=count[i+1]+1,那么孩子的糖果数数组应该为:[1,2,2,1],显然这是错误的。
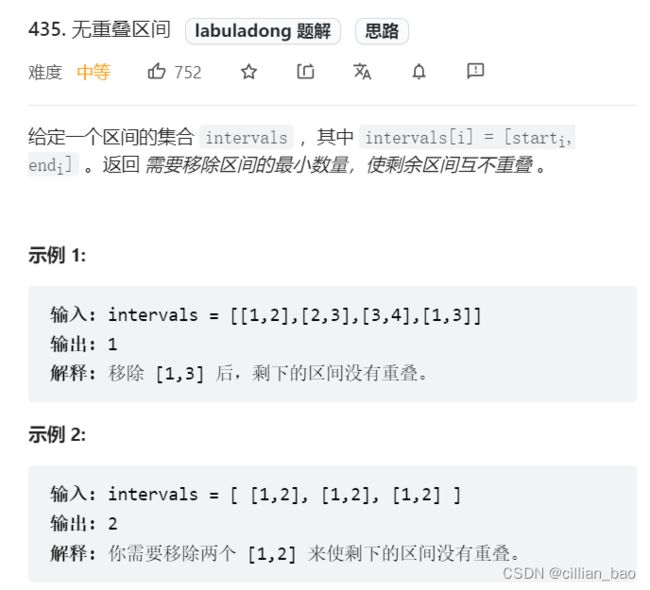
5、无重叠区间
无重叠区间是一道非常典型的贪心算法应用实例。这道题首先映入眼帘的就是这是一道最值问题,那么对于最值问题,我们首先想到的是动态规划,那么这道题绝对是可以使用动态规划去做的。如同最长递增子序列这道题一样,这道题单纯的使用动态规划是比较难得,需要使用二分查找类型的动态规划。
那么对于这道题的贪心算法,和前面几道题类似,最短(最长问题的反问题)这一类的题目,一定是有一个前后的层次递进关系的,这一次的最长、最短结果的值(中间值)一定是要传递到下一次判断中去。
举几个例子:本文的第一题:最长摆动序列,这道题层次递进的是上一次的差值curdiff,作为这一次的prediff,这样才能保证前后的关联性,这样才能是全局的最大值,如果没有前后的关联性,怎么能叫全局的最大值呢。
本文的第二题、第三题,跳跃游戏与跳跃游戏的变体,这两道题中都有这样一段代码
k=Math.max(k,i+nums[i]);
这段代码的主要作用就在于将上一次可跳跃的最大长度和这一次可跳跃的长度机型层次递进,取其大者。这道题与上面几乎是同一个思路。
class Solution{
public int eraseOverlapIntervals(int[][] intervals) {
//首先对其进行排序,按照先结束的排在前面的原则进行排序的规则
Arrays.sort(intervals,new Comparator<int []>(){
public int compare(int []o1,int []o2)
{
return o1[1]-o2[1];
}
});
int count=1;
int end=intervals[0][1];
for(int []e:intervals)
{
int start=e[0];
if(start>=end)
{
count++;
end=e[1];
}
}
return count;
}
}
6、用最少数量的箭射爆气球
class Solution {
public int findMinArrowShots(int[][] points) {
//和无重叠区间特别像
Arrays.sort(points,new Comparator<int[]>(){
public int compare(int []o1,int []o2)
{
return Integer.compare(o1[0], o2[0]);
}
});
int count=1;
for(int i=1;i<points.length;i++)
{
if(points[i][0]>points[i-1][1])
{
count++;
}
else {
points[i][1] = Math.min(points[i][1],points[i - 1][1]);
}
}
return count;
}
}
但是这道题有一个值得注意的地方就是我们再排序的时候,不能用简单的
return o1[0]-o2[0];
由于测试用例出现了[[-2147483646,-2147483645],[2147483646,2147483647]],这样比较大小,一个特别大的正数减去一个特别大的负数出现的值会出现溢出。
这个问题的解决,有两种方法:
第一种就如同解决代码中的用Integer包装类的方法进行比较
第二种:
Arrays.sort(points,new Comparator<int[]>(){
public int compare(int []o1,int []o2)
{
if(o1[0]>o2[0])
{
return 1;
}
else if(o1[0]<o2[0])
{
return -1;
}
else
{
return 0;
}
}
});
7、柠檬水找零

这道题从逻辑上来讲不是难题,但是我们有一个容易出错的点在于就算我现在手上的钱大于这个要找零的这个钱,也并不一定能找零成功。举一个例子:
对于bills= [5,5,10,10,20]而言,当4次交易过后,我们手上的钱只剩两张10快的,最后一次我们收入一张20的,需要我们找零,能满足条件的应该是一张10元、一张5元的或者三张5元的,但是手里没有5元的,故失败。
所以从逻辑上来讲不是说现存手上的钱的总和大于当次收入的钱就可以,而是要有相应的金额组成。
class Solution {
public boolean lemonadeChange(int[] bills) {
int x=0;
int y=0;
int z=0;
for(int bill:bills)
{
if(bill==5)
{
x++;
}
else if(bill==10)
{
y++;
x--;
}
else if(bill==20)
{
//贪的是什么,这一块能不能看出来,就是贪10块先找
if(x>0 && y>0)
{
x--;
y--;
}
else
{
x-=3;
}
}
if(x<0 || y<0)
{
return false;
}
}
return true;
}
}