ST-GCN 论文解读

• 论文名称：Spatial Temporal Graph Convolutional Networks for Skeleton-Based Action Recognition
• 论文下载：https://arxiv.org/pdf/1801.07455.pdf
• 论文代码：https://github.com/yysijie/st-gcn

论文：基于骨骼动作识别的时空图卷积网络

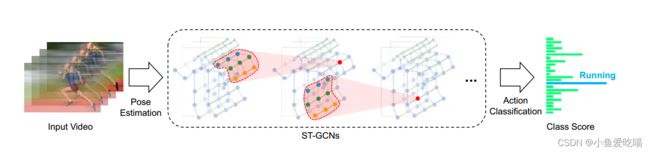
• 对视频进行姿态估计，在骨架序列上构造时空图；
• 在输入数据上应用多层时空图卷积(ST-GCN)，逐步在图上生成更高层次的特征图；
• 然后由标准 $Softmax$ 分类器将其分类到相应的动作类别。
• 整个模型采用反向传播的端到端方式训练。

ST-GCN 的输入通常为三维的骨架关节点矩阵，用于表示人体在时间序列上的运动状态。对于一个长度为 $T$ 的时间序列和 $V$ 个骨架节点，ST-GCN 的输入矩阵为 $X\in R^{V\times C\times T}$，其中 $C$ 表示每个节点的特征维度。如果需要使用 $N$ 个人体的骨架数据进行训练或预测，则可以将这些数据串联成一个四维张量 $X\in R^{N\times V\times C\times T}$ 作为模型的输入。

摘要

传统的骨骼建模方法通常依赖于手工制作的部件或遍历规则，从而导致表达能力有限和泛化困难，针对特定应用设计的模型很难推广到其他应用。

在这项工作中，我们提出了一种新的动态骨架模型，称为时空图卷积网络(ST-GCN)，它通过自动从数据中学习空间和时间模式，超越了以前方法的限制。这种提法不仅具有更强的表达能力，而且具有更强的泛化能力。

主要贡献

这项工作的主要贡献在于三个方面：

• 提出了 ST-GCN，这是一种基于图的动态骨骼建模通用公式，这是第一个将基于图的神经网络应用于该任务。
• 针对骨架建模的具体要求，提出了 ST-GCN 中卷积核的设计原则。
• 在基于骨骼的动作识别的两个大规模数据集上，与之前使用手工制作部件或遍历规则的方法相比，所提出的模型获得了更好的性能，在手工设计方面的工作量大大减少。ST-GCN 的代码和模型是公开的。

ST-GCN：基于图的动态骨骼建模通用公式

在本文中，我们提出通过将图神经网络扩展到时空图模型，设计一种用于动作识别的骨架序列的通用表示，称为时空图卷积网络(ST-GCN)。

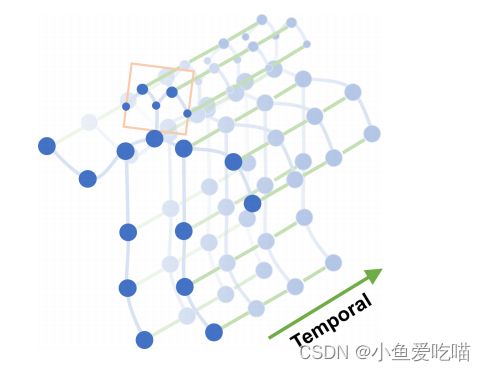
如下图骨架序列的时空图所示，该模型建立在一系列骨架图之上，其中每个节点对应于人体的一个关节。

边有两种类型，

• 一种是符合关节自然连通性的空间边；
• 另一种是跨越连续时间步长连接相同关节的时间边。

在此基础上构造多层时空图卷积，实现了信息在空间和时间维度上的集成。关节坐标被用作 ST-GCN 的输入。

ST-GCN 的层次特性消除了手工制作的部件分配或遍历规则的需要。（不理解看下面的引用）

传统的骨架模型方法中，一般使用基于关键点检测的算法（如 OpenPose 等）来提取人体骨架信息，并根据预定义的部件分配和遍历规则对骨架进行建模。

具体来说，这些规则包括了：

1. 人体骨架的构成方式和连接顺序。
2. 节点对应的身体部位、编号和名称等信息。
3. 骨架节点的搜索顺序和遍历方式。

---

例如，一个典型的手工制作的部件分配或遍历规则可能会指定：躯干部分的关节连接按照肩膀和髋部的关节来确定，手臂部分的关节连接按照肩膀和肘部的关节来确定，腿部分的关节连接按照髋部和膝盖的关节来确定。

而 ST-GCN 的重要作用之一就是在这个基础上，利用时空图卷积网络来动态地学习现有数据中的关系特征，从而消除了手工制作部件分配或遍历规则的需要，提高了行为识别的准确性和稳定性。
(不懂，ST-GCN 是在这个基础上，得到的时空图，那不还是需要部件分配或遍历规则吗？怎么说消除了呢？没错，接着看解释在下面)

---

ST-GCN 在进行时空图卷积之前，仍然需要对骨架节点进行部件分配和遍历规则的设计。不过区别于传统方法中的手工制作，ST-GCN 可以通过学习来动态地确定部件分配和遍历规则，并且这些规则是与特定任务（如行为识别）紧密相关的。

---

类比 CNN 中卷积核的参数，在传统的 CNN 中，卷积核的参数往往需要人工设计，而在使用前向传播和梯度下降等方法进行训练后，CNN 可以自动学习到卷积核的参数。

具体而言，ST-GCN 的部件分配规则通常指定了每个节点的身体部位、编号和名称等信息，例如第一个节点代表头部（Head），第二个节点代表左手肩（Left Shoulder），第三个节点代表右手肩（Right Shoulder）等。

---

而遍历规则则指定了卷积神经网络在时空图上进行卷积运算时的搜索顺序和方式，例如从头部一步步延伸到脚部，或者从中心节点向四周扩散等。

至此，不难理解，为什么说 ST-GCN 是基于图的动态骨骼建模通用公式，就是因为 ST-GCN 利用时空图卷积网络的框架，将关键点（即人体骨架节点）作为节点，通过连接方式建立起空间和时间上的邻接关系，形成了一个时空图。在这个时空图上进行卷积运算，可以动态地学习骨架节点之间的关系特征，有效地学习到人体姿态和动作的空间和时间表达式。

现在我们将讨论 ST-GCN 模型中的组件。

1. 骨架图构建

骨骼序列通常由每一帧中每个人体关节的 2D 或 3D 坐标表示。在我们的工作中，我们利用时空图来形成骨架序列的层次表示。特别地，我们在具有 $N$ 个关节和 $T$ 个框架（帧）的骨架序列上构造了无向时空图 $G=(V,E)$，该骨架序列具有体内和帧间连接。

1.1 节点集 $V$

在这个图中，节点集 $V=\{v_{ti}|t=1，\dots ，T;i=1，\dots ，N\}$ 包括骨架序列中的所有关节。作为 ST-GCN 的输入，节点 $F(v_{ti})$ 上的特征向量由帧 $t$ 上第 $i$ 个关节的坐标向量和估计置信度组成。

置信度是指一个人体关键点被正确预测的程度。它用来代表特征点的识别准确程度和可信度，通常表示为0到1之间的数值。如果置信度越高，说明该关节点被正确识别的概率越大，反之则说明该关节点可能被错误识别或者无法识别。

---

在计算机视觉任务中，对于人体关键点检测问题，置信度 C_conf 通常表示检测算法对于该特定关键点的预测可信度。例如，如果一个人体姿态估计算法可以正确地检测出某个人的肘部关键点，则这个肘部关键点的 C_conf 值应该是比较高的。

我们分两步构建骨架序列上的时空图：

• 首先，根据人体结构的连通性，将一个框架内的关节用边连接起来；
• 然后将每个关节连接到连续帧中的相同关节。

因此，这个设置中的连接是自然定义的，无需手动分配。这也使得网络架构能够在具有不同数量的关节或关节连接的数据集上工作。例如，

• 在动力学数据集上，我们使用来自 $OpenPose$ 工具箱的 2D 姿态估计，结果输出18个关节；
• 而在 NTURGB+D 数据集上，我们使用 3D 关节跟踪结果作为输入，得到25个关节。

ST-GCN 可以在两种情况下操作，并提供一致的优越性能。

1.2 边集 $E$

从形式上讲，边集 $E$ 由两个子集组成：

• 第一个子集描述了每一帧的骨架内连接，记为 $E_S=\{v_{ti}{v}_{tj}|(i,j)\in H\}$，其中 $H$ 为自然连接的人体关节集合；
• 第二个子集包含帧间边，它们连接连续帧中的相同关节，如 $E_F=\{v_{ti}{v}_{(t+1)i}\}$。

因此，对于一个特定关节 $i$，$E_F$ 中的所有边将表示其随时间的轨迹。

2. 空间图卷积神经网络

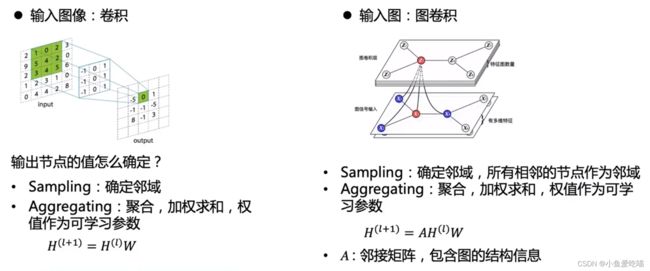
在深入研究成熟的 ST-GCN 之前，我们首先看一下单帧内的图 CNN 模型。在这种情况下，在时间 $\tau$ 的单个帧上，将有 $N$ 个关节节点 $V_t$，以及骨架边 $E_S(\tau )=\{v_{ti}{v}_{tj}|t=\tau ，(i,j)\in H\}$。回顾二维自然图像或特征图上卷积运算的定义，它们都可以被视为二维网格。卷积运算的输出特征图同样是一个二维网格。使用步长 1 和适当的填充，输出特征映射可以与输入特征映射具有相同的大小。在接下来的讨论中，我们将假设这个条件。给定核尺寸为 $K\times K$ 的卷积算子，以及通道数量为 $c$ 的输入特征映射 $f_{in}$。在空间位置 $x$ 处，单个通道的输出值可以写成：
$$f_{out}(x)=\sum _{h=1}^K\sum _{w=1}^K{f}_{in}(\mathbf{p}(\mathbf{x},h,w))\cdot \mathbf{w}(h,w)\text{\hspace{1em}(1)}$$ 抽样函数 $\mathbf{p}：Z^2\times Z^2\to Z^2$ 列举了空间位置 $x$ 的邻居的位置。在图像卷积，它也可以表示为 $\mathbf{p}(\mathbf{x},h,w)=\mathbf{x}+{\mathbf{p}}^{\prime }(h,w)$。权函数 $\mathbf{w}:Z^2\to {\mathbb{R}}^c$ 提供了一个 $c$ 维实空间中的权向量，用于计算与采样的 $c$ 维输入特征向量的内积。注意，权函数与输入位置 $x$ 无关。因此，在输入图像滤波器权重到处都是共享的。图像域上的标准卷积是通过在 $\mathbf{p}(\mathbf{x})$ 中编码一个矩形网格来实现的。

可以理解为：图像域上的标准卷积操作可以看作是将一个大小为 $K\times K$ 的矩阵（即卷积核）沿着图像平面上的每个像素点进行移动，并分别与该像素点周围的一小块区域做内积运算。

然后，通过将上述公式扩展到输入特征映射位于空间图 $V_t$ 上的情况，来定义图上的卷积操作。即特征映射 $f_{in}^t：V_t\to R^c$ 在图的每个节点上都有一个向量。扩展的下一步是重新定义抽样函数 $\mathbf{p}$ 和权重函数 $\mathbf{w}$。

$R^c$ 表示 $c$ 维实数向量空间，其中 $R$ 表示实数域，$c$ 表示向量维度。这里，在第 $t$ 帧，每个关节点可以映射到它的邻接关节点，但是一个关节点需要 $c$ 维（即关节点的坐标和置信度）来表示，所以这是一个 $c$ 维实数向量。

2.1 抽样函数

在图像上，采样函数 $\mathbf{p}(h,w)$ 是在相邻像素点关于中心位置 $x$ 上定义的。在图上，我们同样可以在节点 $v_{ti}$ 的邻居集 $B(v_{ti})=\{v_{tj}|d(v_{tj},v_{ti})\le D\}$ 上定义采样函数。这里 $d(v_{tj},v_{ti})$ 表示从 $v_{tj}$ 到 $v_{ti}$ 的任何路径的最小长度。因此，抽样函数 $\mathbf{p}:B(v_{ti})\to V$ 可以写成：
$$\mathbf{p}(v_{ti},v_{tj})=v_{tj}\text{\hspace{1em}(2)}$$

注意这里的 $v_{tj}$ 是节点 $v_{ti}$ 的邻居集 $B(v_{ti})$中的节点，即当 $D=1$ 时，采样函数 $\mathbf{p}$ 取的是邻接点。

在这项工作中，我们对所有情况使用 $D=1$，即关节节点的 $1-neighbor$ 集。更大的 $D$ 值留给以后的工作。

2.2 权重函数

与抽样函数相比，权重函数的定义比较复杂。在二维卷积中，中心位置周围自然存在一个刚性网格。所以相邻的像素可以有固定的空间顺序。权重函数可以通过根据空间顺序索引$(c,K,K)$ 维的张量来实现。

对于一般的图，就像我们刚刚构造的那样，没有这样的隐式排列。这个问题的解决方案首先在 (Niepert, Ahmed, and Kutzkov 2016) 中进行了研究，其中顺序由该关节点周围的邻居图中的图标记过程定义。我们按照这个思路来构造权重函数。我们没有给每个邻居节点一个唯一的标签，而是将一个关节点 $v_{ti}$ 的邻居集 $B(v_{ti})$ 划分为固定数量的 $K$ 个子集，其中每个子集都有一个数字标签，从而简化了这个过程。

因此，我们可以得到一个映射 $l_{ti}：B(v_{ti})\to \{0，\dots ，K-1\}$，它将邻域中的一个节点映射到它的子集标签。权函数 $\mathbf{w}(v_{ti},v_{tj}):B(v_{ti})\to R^c$ 可以通过索引一个 $(c,K)$ 维张量或
$$\mathbf{w}(v_{ti},v_{tj})={\mathbf{w}}^{\prime }(l_{ti}(v_{tj}))\text{\hspace{1em}(3)}$$
来实现。

这里解释一下，如果我们使用一个 $(c,K)$ 维张量 ${\mathbf{w}}^{\prime }$ 来表示权重向量 $\mathbf{w}$，其中第 $k$ 个列向量为 ${\mathbf{w}}_k^{\prime }$ ，则表达式(3)的意思是：对于给定的关节点 $v_{ti}$ 和邻居节点 $v_{tj}$，我们首先计算出 $v_{tj}$ 的子集标签 $l_{ti}(V_{tj})$，然后使用这个标签来索引张量 ${\mathbf{w}}^{\prime }$ 中的一个列向量 ${\mathbf{w}}_{l_{ti}(v_{tj})}^{\prime }$ ，从而得到节点 $v_{ti}$ 和 $v_{tj}$ 之间的权重向量 $\mathbf{w}(v_{ti},v_{tj})$。

我们将在下面讨论几种分区策略。

2.3 空间图卷积

有了改进的抽样函数和权函数，我们现在用图卷积重写公式(1)如下：
$$f_{out}(v_{ti})=\sum _{v_{tj}\in B(v_{ti})}\frac{1}{Z_{ti}(v_{tj})}{f}_{in}(\mathbf{p}(v_{ti},v_{tj}))\cdot \mathbf{w}(v_{ti},v_{tj})\text{\hspace{1em}(4)}$$ 其中归一项 $Z_{ti}(v_{tj})=|v_{tk}|l_{ti}(v_{tk})=l_{ti}(v_{tj})|$ 等于相应子集的基数。添加这个术语是为了平衡不同子集对输出的贡献。

将公式(2)和公式(3)代入公式(4)，得到
$$f_{out}(v_{ti})=\sum _{v_{tj}\in B(v_{ti})}\frac{1}{Z_{ti}(v_{tj})}{f}_{in}(v_{tj})\cdot \mathbf{w}(l_{ti}(v_{tj}))\text{\hspace{1em}(5)}$$值得注意的是，如果我们将图像视为一个规则的 2D 网格，这个公式可以类似于标准的 2D 卷积。例如，为了类似于3×3卷积运算，我们在以像素为中心的3×3网格中有一个9像素的邻居。然后将邻居集划分为9个子集，每个子集有一个像素。

2.4 时空建模

在时空图中，考虑每个节点不仅具有空间位置信息，还具有时间信息。因此，我们需要重新定义邻域 $B(v_{ti})$，以包括时间上相邻的节点，即连接连续帧上的相同关节。

已经制定了空间图 CNN，我们现在推进到在骨架序列内建模时空动态的任务。回想一下，在图的构造中，图的时间方面是通过连接连续帧上的相同关节来构造的。这使我们能够定义一个非常简单的策略来将空间图 CNN 扩展到时空域。

也就是说，我们扩展了邻域的概念，也包括时间连接的关节为
$$B(v_{ti})=\{v_{qj}|d(v_{tj},v_{ti})\le K,|q-t|\le \lfloor \Gamma /2\rfloor \}\text{\hspace{1em}(6)}$$该公式定义了每个节点的邻域 $B(v_{ti})$ 包括空间距离不超过 $K$ 个单位的所有节点和时间距离不超过 $\lfloor \Gamma /2\rfloor$ 个单位的所有节点。其中，参数 $\Gamma$ 控制时间上要包含在邻域图中的范围，因此可以称为时间内核大小。

为了在时空图上完成卷积运算，我们需要类比空间图的方法，定义采样函数和权重函数。与空间图一样，采样函数是一个简单的函数，不需要任何修改。获得邻居节点的方法与空间图相同，只需使用表达式(6)中定义的邻域来获取。

我们需要修改标签映射，以适应带时间维度的邻域。由于时间轴是有序的，对于以 $v_{ti}$ 为中间位置的空间时间邻域，我们直接修改标签映射 $l_{ST}$，为： $$l_{ST}(v_{qj})=l_{ti}(v_{tj})+(q-t+\lfloor \Gamma /2\rfloor )\times K\text{\hspace{1em}(7)}$$其中 $l_{ti}(v_{tj})$ 是在一个单帧 $t$ 上关节 $i$ 的邻接点 $j$ 的标签映射，而 $(q-t+\lfloor \Gamma /2\rfloor )\times K$ 用于在时间维度上对标签进行编码。这样，我们就对所构造的时空图进行了定义良好的卷积运算。

由于时空图中每个节点都包含了时间信息，而且时间轴是有序的，因此我们需要一种方式来将时间信息编码进标签映射里，从而使得卷积运算能够顺利进行。

---

这里解释一下具体方法：在节点 $v_{ti}$ 的标签映射 $l_{ti}(v_{tj})$ 的基础上，加上一个时间维度的偏移量 $(q-t+\lfloor \Gamma /2\rfloor )\times K$ 。这个公式中，

• $q$ 表示当前样本节点 $v_{qj}$ 在时空图中所处的时间步（帧）数，也可以理解为当前处理的时刻，通常是通过滑动一个窗口来进行遍历处理。
• $t$ 表示 $v_{ti}$ 所处的时间步（帧）数。
• 因此，$q-t$ 就是当前节点 $v_{qj}$ 与节点 $v_{ti}$ 之间的时间距离。对于当前节点 $v_{qj}$，它的时间邻域可以由 $(q-\lfloor \Gamma /2\rfloor ,q+\lfloor \Gamma /2\rfloor )$ 表示。
• 再加上 $\lfloor \Gamma /2\rfloor$ 是为了获取当前节点的邻域范围，保证时间距离在 $\Gamma$ 范围内，而不会超出有效时间范围。
• 最后再乘以 $K$ 是为了将时间距离转换为标签数值，其中 $K$ 是一个常量，表示每个时间步的标签表示的长度。

---

简单来说，$(q-t+\lfloor \Gamma /2\rfloor )\times K$ 这个公式的作用就是将时间信息编码为标签数值，从而方便在时空图上进行卷积运算。

3. 分区策略（ST-GCN 中卷积核的设计原则）

考虑到时空图卷积的高级形式，设计一种划分策略来实现标签映射 $l$ 是很重要的。在这项工作中，我们探索了几种划分策略。为了简单起见，我们只讨论单个框架中的情况，因为它们可以使用公式(7)自然地扩展到时空域。

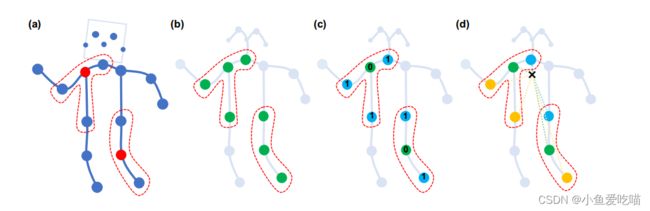
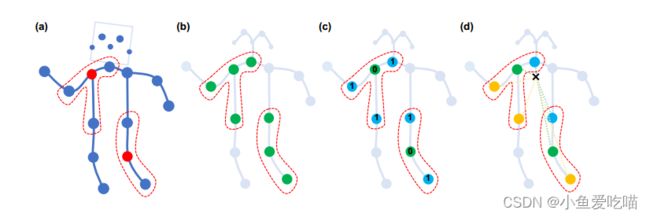
上图是构造卷积运算的划分策略。从左到右：

• （a）输入骨架示例帧。身体关节用蓝点绘制。$D=1$ 的过滤器的接受域用红色虚线圈绘制。
• （b）单标签分区策略，即一个邻域内的所有节点都有相同的标签(绿色)。
• （c）距离分区策略，这两个子集是距离为0的根节点本身(绿色)和距离为1的其他相邻点(蓝色)。
• （d）空间结构分区策略，节点根据与骨架重心(黑色十字)的距离与根节点(绿色)的距离进行标记，向心节点的距离较短(蓝色)，而离心节点的距离较长(黄色)。

3.1 Uni-labeling 单标签分区策略

最简单、最直接的划分策略是使用子集，即整个邻居集本身。在这种策略中，每个相邻节点上的特征向量都有一个具有相同权重向量的内积。实际上，这种策略类似于(Kipf和Welling 2017)中引入的传播规则。它有一个明显的缺点，在单帧情况下，使用该策略相当于计算所有相邻节点的权值向量与平均特征向量之间的内积。这对于骨架序列分类来说是次优的，因为在这个操作中可能会丢失局部微分性质。形式上，我们有 $K=1,l_{ti}(v_{tj})=0，\forall i,j\in V$。

3.2 Distance partitioning 距离分区策略

另一种自然划分策略是根据节点到中心位置节点 $v_{ti}$ 的距离 $d(\cdot ，v_{ti})$ 对邻居集进行划分。在这项工作中，因为我们设置 $D=1$，邻居集将被分成两个子集，其中 $D=0$ 表示中心位置节点本身，其余的邻居节点都在 $D=1$ 子集中。因此，我们将有两个不同的权重向量，它们能够建模局部微分性质，如关节之间的相对平移。形式上，我们有 $K=2,l_{ti}(v_{tj})=d(v_{tj},v_{ti})$。

3.3 Spatial configuration partitioning 空间结构分区策略

由于人体骨架在空间上是局部化的，我们仍然可以在分区过程中利用这种特定的空间结构。我们设计了一种策略，将邻居集分为三个子集：1)根节点本身；2)向心群：比根节点更接近骨架重心的相邻节点；3)否则为离心群。在这里，骨架中所有关节的平均坐标被视为其重心。这种策略的灵感来自于身体部位的运动可以大致分为同心运动和偏心运动。形式上，我们有：$$l_{ti}(v_{tj})=\{\begin{array}{ll}0,& r_j=r_i\\ 1,& r_j<r_i\\ 2,& r_j>r_i\end{array}\text{\hspace{1em}(8)}$$
其中 $r_i$ 是训练集中所有帧中从重心到关节 $i$ 的平均距离。

更先进的分区策略有望带来更好的建模能力和识别性能。

4. 可学习边缘重要性加权

在动作的过程中，一个关节可能会在身体的多个部位出现。而且，在不同部位的动力学建模中，这些关节外观的重要性是不同的。在这个意义上，我们在时空图卷积的每一层上都加上一个可学习的掩码 $M$。

掩码将根据 $E_S$ 中每个空间图边的学习重要性权重，将节点的特征贡献扩展到其邻近节点。这样就能更好地处理不同部位之间的关节信息。我们发现添加该掩码可以进一步提高 ST-GCN 的识别性能。

也可以使用一个依赖于数据的注意力图，来提升空间特征的贡献扩展效果。注意力图可以帮助模型更准确地关注重要的特征信息，从而提高性能表现。我们把这个留给未来的工作。

实现 ST-GCN

基于图的卷积的实现不像 2D 或 3D 卷积那样简单。在这里，我们提供了实现 ST-GCN 用于基于骨架的动作识别的细节。

我们采用类似于(Kipf和Welling 2017)中的图卷积实现。单帧内关节的体内连接由表示自连接的邻接矩阵 $\mathbf{A}$ 和单位矩阵 $\mathbf{I}$ 表示。在单帧情况下，采用第一个分区策略的 ST-GCN 可以用以下公式实现 $${\mathbf{f}}_{out}={\mathbf{\Lambda }}^{-\frac{1}{2}}(\mathbf{A}+\mathbf{I}){\mathbf{\Lambda }}^{-\frac{1}{2}}{\mathbf{f}}_{in}\mathbf{W}\text{\hspace{1em}(9)}$$其中 ${\Lambda }^{ii}={\sum }_j(A^{ij}+I^{ij})$。这里将多个输出通道的权值向量叠加形成权值矩阵 $\mathbf{W}$。在实际操作中，在时空情况下，我们可以将输入特征映射表示为 $(C,V,T)$ 维的张量。图卷积是通过执行 $1\times \Gamma$ 标准 2D 卷积来实现的，并将得到的张量与第二维上的归一化邻接矩阵 ${\mathbf{\Lambda }}^{-\frac{1}{2}}(\mathbf{A}+\mathbf{I}){\mathbf{\Lambda }}^{-\frac{1}{2}}$ 相乘。

对于具有多个子集的分区策略，即距离分区和空间结构分区，我们再次利用了这种实现。但注意，现在邻接矩阵被分解成几个矩阵，其中 $\mathbf{A}+\mathbf{I}={\sum }_j{\mathbf{A}}_j$。例如，在距离划分策略中，${\mathbf{A}}_0=\mathbf{I},{\mathbf{A}}_1=\mathbf{A}$，表达式(9)转换成：$${\mathbf{f}}_{out}=\sum _j{\mathbf{\Lambda }}_j^{-\frac{1}{2}}{\mathbf{A}}_j{\mathbf{\Lambda }}_j^{-\frac{1}{2}}{\mathbf{f}}_{in}{\mathbf{W}}_j\text{\hspace{1em}(10)}$$ 其中，类似地 ${\Lambda }_j^{ii}={\sum }_k(A_j^{ik})+\alpha$。这里我们设 $\alpha =0.001$ 以避免 $A_j$ 中的空行。

可学习边缘重要性加权的实现非常简单。对于每个邻接矩阵，我们都伴随一个可学习权值矩阵 $\mathbf{M}$，我们分别用 $(\mathbf{A}+\mathbf{I})\otimes \mathbf{M}$ 和 ${\mathbf{A}}_j\otimes \mathbf{M}$ 代替表达式(9)中的矩阵 $\mathbf{A}+\mathbf{I}$ 和表达式(10)中的 ${\mathbf{A}}_j$ 。这里 $\otimes$ 表示两个矩阵之间的元素乘积。掩码 $M$ 被初始化为一个全一矩阵。

网络架构与训练

由于 ST-GCN 在不同节点上共享权重，因此在不同节点上保持输入数据的比例一致是很重要的。在我们的实验中，我们首先将输入骨架提供给批处理规范化层来规范化数据。

ST-GCN 模型由9层时空图卷积算子(ST-GCN 单元)组成。前三层有64个输出通道，接着三层有128个输出通道，最后三层有256个输出通道。这些层有9个时间内核大小。Resnet 机制应用于每个 ST-GCN 单元。

在每个 ST-GCN 单元后，我们以0.5概率随机剔除特征，以避免过拟合。第4和第7时序卷积层的步长设为2作为池化层。然后对得到的张量进行全局池化，得到每个序列的256维特征向量。最后，我们将它们输入 $SoftMax$ 分类器。使用随机梯度下降学习模型，学习率为0.01。我们在每10个 epoch 之后将学习率衰减0.1。

为了避免过拟合，我们在动力学数据集上训练时执行两种增强来替换掉层(Kay et al 2017)。

首先，为了模拟相机运动，我们对所有帧的骨架序列执行随机仿射变换。特别是从第一帧到最后一帧，我们选取了几个固定的角度、平移和比例因子作为候选因子，然后随机采样三个因子的两个组合来生成仿射变换。这种转换被插入到中间帧中，以产生一种效果，就好像我们在回放过程中平滑地移动视点一样。我们把这种增强称为随机移动。

其次，我们在训练中从原始骨架序列中随机抽取片段，并在测试中使用所有帧。网络顶部的全局池使网络能够处理不确定长度的输入序列。

实验

我们评估了 ST-GCN 在基于骨骼的动作识别实验中的性能。我们在两个性质截然不同的大规模动作识别数据集上进行了实验：Kinetics 人类动作数据集(Kinetics) (Kay et al 2017)是迄今为止最大的无约束动作识别数据集，NTURGB+D (Shahroudy et al 2016)是最大的内部捕获动作识别数据集。

特别是，我们首先对动力学数据集进行详细的消融研究，以检查所提出的模型组件对识别性能的贡献。然后我们将 ST-GCN 的识别结果与其他最先进的方法和其他输入模式进行了比较。

为了验证我们在无约束设置中获得的经验是否具有普遍性，我们对 NTURGB+D 上的约束设置进行了实验，并将 ST-GCN 与其他最先进的方法进行了比较。所有实验均在 PyTorch 深度学习框架上进行，并配有8个 TITANX 图形处理器。

论文理解

ST-GCN 这篇论文算是 GCN 在骨骼行为识别里面的开山之作了，他提供了一种新的思路和实现方式，解决了以前方法的局限性并取得了较好的效果。虽然他只是2018年发表的，但是这篇论文给了很详细的代码，2019年发表在 CVPR 上的 AS-GCN 和 2s-AGCN 都是在该代码的基础上改进的。

学习新的东西的时候，将他和学习过的老的东西进行对比。比如学习 GCN 要和之前学过的 CNN 对比着学，就非常好理解。

空间特征的提取

1. 图卷积

特征提取器，输入结点特征和 graph 结构，输出结点最终的特征表达。

主要的框架就是这样，图卷积相比于图像卷积，只是多左乘了一个邻接矩阵 $A$，后面就是一些细节。

如上图所示，

1. 邻接矩阵 $A$ 的对角线都是0，这说明没有考虑自身节点的特征，只是考虑了边的特征。
2. 如果加上自身节点的特征，就是 $A^{\prime }$，即论文中的 $A+I$。
3. 如果再考虑对 $A^{\prime }$ 进行归一化，就是 $D^{-1}{A}^{\prime }$，其中 $D$ 是度矩阵。
4. 对称归一化，如第四个公式所示 $D^{-\frac{1}{2}}{A}^{\prime }{D}^{-\frac{1}{2}}$。

2. 感受野

一般图像二维卷积最小的卷积核就是 $3\times 3$ 的卷积核，感受野就是一个中心点和周围八个元素共九个元素的组合。

这里和CNN相似，定义离中心点距离 $D=1$ ，也就是与中心点直接相连的点为一个卷积核的感受野。如图（a）所示：

3. 卷积核

那么怎么选择卷积核呢？

这里感受野都是离中心点距离 $D=1$ 的范围，选择卷积核就是说将同范围的点进行分类。

• 图（b）是中心点和相连的点采用同样的权重，这里只有一种权重；
• 图（c）是中心点和相连的点采用不同的权重，这里有两种权重；
• 图（d）分为三种点，一是静止点，二是向心点，三是离心点，指的是离人体重心近的点和远的点，所以有三种权重。

从直觉上，图（d）选择方法更加合适。

先计算人体重心位置，即上图中黑色 × 位置。

相对于绿色节点来说：

• 蓝色节点到重心的距离更小，那蓝色节点就是向心点；
• 橙色节点到重心的距离更大，那橙色节点就是离心点；
• 而绿色节点本身就是一个静止的点。

选择合适的感受野和卷积核之后就能够像 CNN 那样一个点一个点的卷积计算了，卷积的过程就是提取特征的过程。

4. 注意力机制

注意力机制，论文上说的是一个可学习的掩码 $M$，加入方式也很简单，就是直接与上面说的 $A^{\prime }$ 相乘。这是一种非常简单的方法，虽然不是最好的，但是用的是最多的。

上面说的都是空间特征的提取，后面要做的就是时间特征的提取。

时间特征的提取

时间特征提取用的是 TCN，是一个 1D 卷积，卷积的维度是时间维度，他的卷积核一行多列，从下图就很容易看明白。

这篇论文其实就这么多内容，喜欢推公式的可以去研究一下论文的公式。

作为一篇开创性的文章，自然也会有很多不足之处，比如他的卷积核选择方式只能聚集局部特征，还有注意力机制并不能创造没有直接相连的关节的联系。

只不过这些都是别人论文总结的，等什么时候自己能分析出缺点和解决办法就离论文不远了。