AVL树的详细实现(C++)
AVL树概念
前面已经介绍了二叉搜索树,但是二叉搜索树在某些情况下会出现极度不平衡,其树形结构便退化成了链表,查找效率也会下降。于是出现了 AVL 树,AVL 树保证了二叉搜索树的平衡,引入了平衡监督机制,也就是在插入结点时,树中某一部分不平衡度超过一个阈值后将出发平衡调整操作,这样便保证了树的平衡度在可接受的范围内,最大的好处就是提高了搜索的效率。
AVL 树是一种平衡二叉树,其名字来源于发明者的名字(Adelson-Velskii 以及 Landis)。AVL树的递归定义如下:
- 左右子树的高度差小于等于 1。
- 其每一个子树均为平衡二叉树。
通过这两个性质就可以判定一棵树是否为平衡二叉树了。
如下图就是一颗平衡二叉树,任何节点的两个子树的高度最大差别为 1:
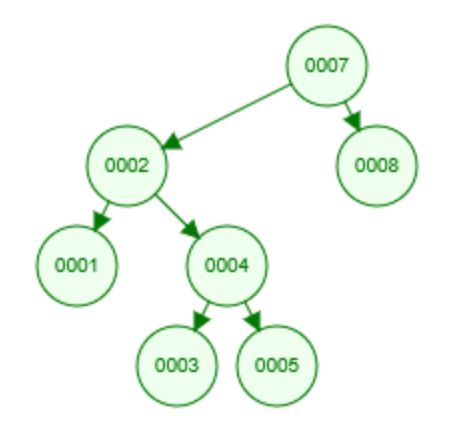
而下图不是一颗平衡二叉树,因为结点 7 的两颗子树高度相差为 2。
AVL 树的查找、插入和删除在平均和最坏情况下均为 O(logn)。
如果在 AVL 树种插入或删除节点后,使得高度之差大于 1。此时,AVL 树的平衡状态就被破坏,不再是平衡二叉树,为了维持一个平衡状态,需要对其进行旋转处理。
平衡二叉树加入了“平衡因子”概念,定义为:
某个结点的左子树的高度减去右子树的高度得到的差值。AVL 树的所有结点的平衡因子的绝对值都不超过 1。
为了计算平衡因子,自然需要在节点种引入高度这一属性。高度一般定义为左右子树高度的最大值。下面将会详细介绍 AVL 树的详细实现。
AVL树的失衡调整
失衡
在 AVL 树中进行插入或删除节点后,可能导致 AVL 树失去平衡。这种失衡可以概括为 4 中姿态:
(1)LL 失衡:LeftLeft,也称为“左左”。插入或删除一个节点后,根节点的左子树的左子树还有非空子节点,导致“根的左子树的高度”比“根的右子树的高度”大 2,导致 AVL 树失去了平衡。如下图:

(2)LR 失衡:LeftRight,也称为“左右”。插入或删除一个节点后,根节点的左子树的右子树还有非空子节点,导致“根的左子树的高度”比“根的右子树的高度”大 2,导致 AVL 树失去了平衡。如下图:
(3)RL 失衡:RightLeft,称为“右左”。插入或删除一个节点后,根节点的右子树的左子树还有非空子节点,导致“根的右子树的高度”比“根的左子树的高度”大 2,导致 AVL 树失去了平衡。
(4)RR 失衡:RightRight,称为“右右”。插入或删除一个节点后,根节点的右子树的右子树还有非空子节点,导致“根的右子树的高度”比“根的左子树的高度”大 2,导致 AVL 树失去了平衡。
旋转
LL 旋转
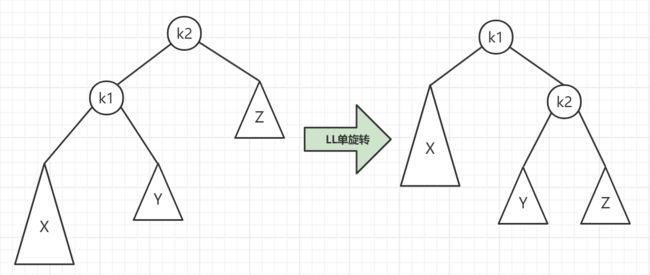
LL 失衡的情况,可以通过一次左旋转将 AVL 树恢复平衡,如下图:
可以发现,只通过一次旋转就可以恢复为 AVL 树。对于 LL 旋转,可以这样理解:
LL 旋转是围绕“失去平衡的 AVL 根节点”进行的,也就是节点 k2,由于是 LL 情况,即“左左情况”,用手抓着“左孩子,即 k1”使劲向左摇,将 k1 变成了根节点,而 k2 变成了 k1 的右子树,而“k1 的右子树”变成了“k2 的左子树”。
代码如下:
AVLTreeNode<T> *leftLeftRotation(AVLTreeNode<T> *&k2)
{
AVLTreeNode<T> *k1 = k2->m_leftChild;
k2->m_leftChild = k1->m_rightNode;
k1->m_rightNode = k2;
k2->m_height = std::max(height(k2->m_leftChild), height(k2->m_rightNode)) + 1;
k1->m_height = std::max(height(k1->m_leftChild), k2->m_height) + 1;
return k1;
}
RR 旋转
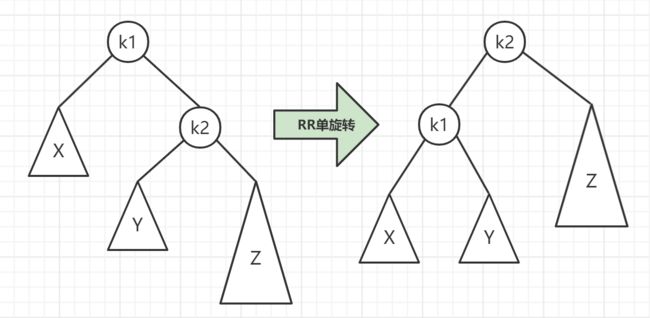
理解了 LL 之后,RR 旋转就相当容易理解了。RR 就是与 LL 堆成的情况,RR 恢复平衡的旋转方法如下:
RR 旋转也只需要一次即可。对于 RR 旋转,可以这样理解:
RR 旋转是围绕“失去平衡的 AVL 根节点”进行的,也就是节点 k1,由于是 RR 情况,即“右右情况”,用手抓着“右孩子,即 k2”使劲向右摇,将 k2 变成了根节点,而 k1 变成了 k2 的左子树,而“k1 的右子树”变成了“k2 的左子树”。
代码如下:
AVLTreeNode<T> *rightRightRotation(AVLTreeNode<T> *&k1)
{
AVLTreeNode<T> *k2 = k1->m_rightNode;
k1->m_rightNode = k2->m_leftChild;
k2->m_leftChild = k1;
k1->m_height = std::max(height(k1->m_leftChild), height(k1->m_rightNode)) + 1;
k2->m_height = std::max(height(k2->m_rightNode), k1->m_height) + 1;
return k2;
}
LR 旋转
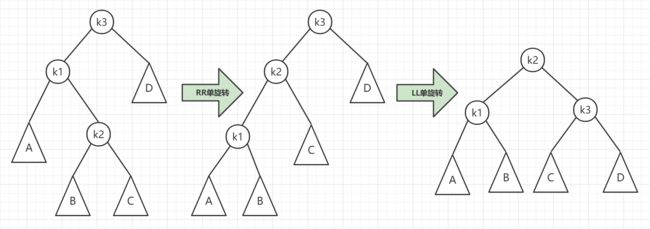
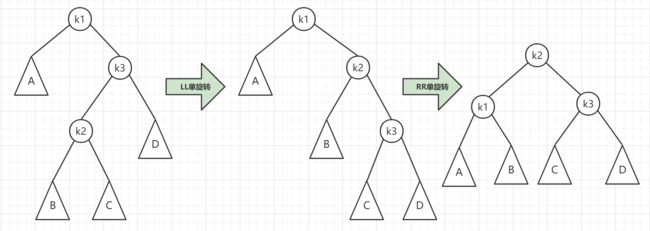
LR 失衡情况,需要经过两次旋转才能让 AVL 树恢复平衡。如下图:
第一次旋转是围绕 k1 进行的 RR 旋转,第二次旋转是围绕 k3 进行的 LL 旋转。
代码如下:
AVLTreeNode<T> *leftRightRotation(AVLTreeNode<T> *&k3)
{
k3->m_leftChild = rightRightRotation(k3->m_leftChild);
return leftLeftRotation(k3);
}
RL 旋转
RL 旋转是和 LR 对称的情况,RL 恢复平衡的旋转方法如下:
第一次旋转是围绕 k3 进行的 LL 旋转,第二次是围绕 k1 进行的 RR 旋转。
代码如下:
AVLTreeNode<T> *rightLeftRotation(AVLTreeNode<T> *&k1)
{
k1->m_rightNode = leftLeftRotation(k1->m_rightNode);
return rightRightRotation(k1);
}
AVL树的实现
节点定义
template <typename T>
struct AVLTreeNode
{
T m_key; // 关键字
int m_height; // 高度
AVLTreeNode *m_leftChild; // 左孩子
AVLTreeNode *m_rightNode; // 右孩子
AVLTreeNode(T value, AVLTreeNode *l, AVLTreeNode *r) : m_key(value), m_height(0), m_leftChild(l), m_rightNode(r) {}
};
详细代码实现
注意:关于 AVL 树的各种二叉树的通用接口之前的二叉树篇幅中已经实现过,这里不再赘述,仅实现了 AVL 树中重要的接口。
#include 参考:
https://wangkuiwu.github.io/2013/02/02/avltree-cpp