python--简单线性回归
新年第一篇
有些敷衍
1.1jupyter notebook
Insert->Insert Cell Below 添加格子;
Cell->Run Cell 运行代码;
Help->Keyboard Shortcuts 快捷键;
编辑->Markdown语法;
2.简单线性回归
线性:经过模型训练,得到自变量和因变量之间是线性关系
回归:根据已知的输入输出的到模型,根据模型进行输入,得到连续的输出
这种关系用于预测未来事件的结果;
线性回归使用数据点之间的关系在所有数据点之间画一条直线,这条线可以用来预测未来的值;
r 平方值(r-squared)的范围是 0 到 1,其中 0 表示不相关,而 1 表示 100% 相关;(糟糕的拟合度比如0.013 表示关系很差,并告诉我们该数据集不适合线性回归);
回归方程:y=c+m1x1+m2x2+mm*xn(m1是第一个特征,mn是第n个特征)
优点:在数据量大的情况下速度依然很快,不需要很复杂的计算,可以根据系数给出每个变量的理解和解释;
缺点:不能很好地拟合非线性数据,所以需要先判断变量之间是否是线性关系;
2.1
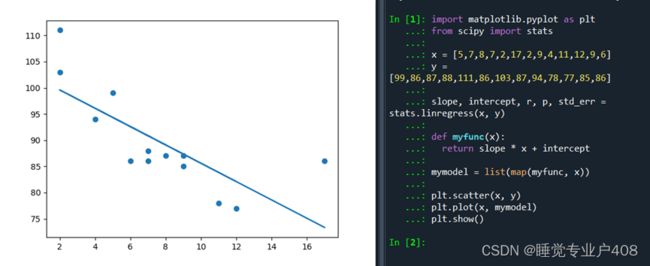
import matplotlib.pyplot as plt
from scipy import stats
//导入需要的模块
x = [5,7,8,7,2,17,2,9,4,11,12,9,6]
y = [99,86,87,88,111,86,103,87,94,78,77,85,86]
//数据
slope, intercept, r, p, std_err = stats.linregress(x, y)
//返回一些重要的键值,例:print(r)可以看拟合度
def myfunc(x):
return slope * x + intercept
//一个返回相对应x的值将在y轴上放置的新值的函数
mymodel = list(map(myfunc, x))
//产生一个新的数组,其中y轴具有新值
plt.scatter(x, y)//绘制原始散点图
plt.plot(x, mymodel)//绘制线性规划线
plt.show()//显示图
2.2 多元回归
import pandas
df = pandas.read_csv(r"C:\Users\罗依婧\Desktop\meeee\cars.csv")
X = df[['Weight','Volume']]
y = df['CO2']//通常,将独立值列表命名为大写X,将相关值列表命名为小写y
from sklearn import linear_model
regr = linear_model.LinearRegression()
regr.fit(X,y)
predictedCO2 = regr.predict([[2300,1300]])
print(predictCO2)
print(regr.coef_)
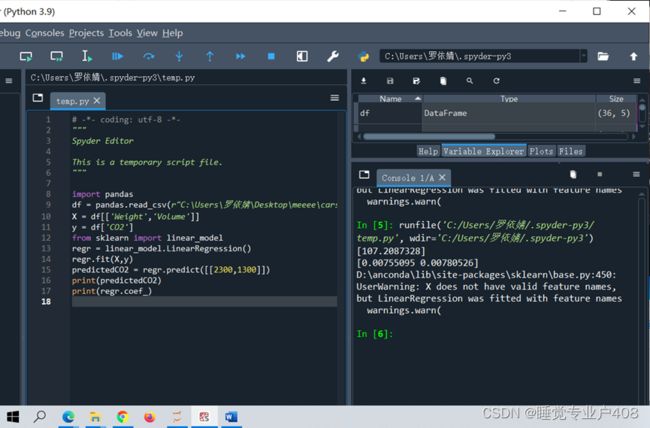
从图中可得:如果一辆配备 1300ccm 发动机的汽车重 2300 千克,则二氧化碳排放量将约为 107g
如果重量增加 1g,则 CO2 排放量将增加 0.00755095g。
如果发动机尺寸(容积)增加 1 ccm,则 CO2 排放量将增加 0.00780526g
2.3 价格预测:
根据面积预测总价
import numpy as np
from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
//导入模块
x = np.array([6,16,26,36,46,56]).reshape((-1,1))
y = np.array([4,23,10,12,22,35])
plt.scatter(x,y)
plt.show()
//导入数据并绘制散点图
model = LinearRegression().fit(x,y)//创建模块并拟合
r_sq = model.score(x,y)
print('确定系数:',r_sq)//评估模型
print('截距:',model.intercept_)
print('斜率:',model.coef_)
y_pred = model.predict(x)
print('预测结果:',y_pred,sep = '\n')//获取模型中的参数