【机器学习(三)】基于线性回归对波士顿房价预测
文章目录
- 专栏导读
- 1、线性回归原理
- 2、实战案例
-
- 2.1数据说明
- 2.2导入必要的库并加载数据集
- 2.3划分训练集和测试集
- 2.4创建线性回归模型
- 2.5模型预测评价
专栏导读
✍ 作者简介:i阿极,CSDN Python领域新星创作者,专注于分享python领域知识。
✍ 本文录入于《数据分析之术》,本专栏精选了经典的机器学习算法进行讲解,针对大学生、初级数据分析工程师精心打造,对机器学习算法知识点逐一击破,不断学习,提升自我。
✍ 订阅后,可以阅读《数据分析之术》中全部文章内容,详细介绍数学模型及原理,带领读者通过模型与算法描述实现一个个案例。
✍ 还可以订阅基础篇《数据分析之道》,其包含python基础语法、数据结构和文件操作,科学计算,实现文件内容操作,实现数据可视化等等。
✍ 其他专栏:《数据分析案例》 ,《机器学习案例》
1、线性回归原理
线性回归是一种经典的机器学习算法,用于建立一个线性关系模型,以预测一个连续型变量的值。它的基本假设是,目标变量和特征变量之间存在线性关系,即目标变量可以通过特征变量的线性组合来进行预测。
线性回归模型的一般形式可以表示为:
y y y = β 0 + β 1 x 1 + β 2 x 2 + . . . + β p x p + ϵ \beta_0+ \beta_1x_1+\beta_2x_2+ ...+ \beta_px_p +\epsilon β0+β1x1+β2x2+...+βpxp+ϵ
y y y 是目标变量, x 1 , x 2 , . . . , x p x_1, x_2, ..., x_p x1,x2,...,xp 是特征变量, β 0 , β 1 , β 2 , . . . , β p \beta_0, \beta_1, \beta_2, ..., \beta_p β0,β1,β2,...,βp 是模型的系数, ϵ \epsilon ϵ 是误差项。模型的目标就是找到最优的系数 β 0 , β 1 , β 2 , . . . , β p \beta_0, \beta_1, \beta_2, ..., \beta_p β0,β1,β2,...,βp 来最小化误差项。
线性回归模型的训练过程就是根据已有的数据集,求解出最优的模型系数。常用的方法有最小二乘法和梯度下降法。
-
最小二乘法是一种直接求解解析解的方法,即通过对误差的平方和进行求导,得到系数的解析解。
-
梯度下降法则是一种迭代优化的方法,通过不断地沿着误差梯度的反方向更新系数,逐步优化模型。
线性回归模型的预测过程就是根据已有的模型系数,对新的特征数据进行预测。具体而言,将新的特征数据代入模型,计算出目标变量的预测值。
线性回归模型的优点是:
- 简单
- 易于解释
- 计算快速
它的缺点也很明显:
- 就是只能处理线性关系,对于非线性数据的拟合效果较差
- 它也很容易受到异常值的影响,需要进行特殊的处理。
2、实战案例
2.1数据说明
波士顿房价数据集的13个特征如下:
| 标签 | 说明 |
|---|---|
| CRIM | 城镇人均犯罪率 |
| ZN | 住宅用地占地面积的比例 |
| INDUS | 城镇中非住宅用地的比例 |
| CHAS | 是否靠近河边(如果是则为1,否则为0) |
| NOX | 一氧化氮浓度 |
| RM | 每栋住宅的平均房间数 |
| AGE | 1940年以前建成的自住单位比例 |
| DIS | 到五个波士顿就业中心的加权距离 |
| RAD | 到辐射道路的可达性指数 |
| TAX | 每一万美元的不动产税率 |
| PTRATIO | 城镇中的学生与教师比例 |
| B | 黑人比例 |
| LSTAT | 地区中有多少百分比的人属于低收入阶层 |
2.2导入必要的库并加载数据集
我们需要导入必要的库并加载数据集。代码如下:
import numpy as np
import pandas as pd
from sklearn.datasets import load_boston
# 加载数据集
boston = load_boston()
load_boston函数会返回一个Bunch对象,其中包含了波士顿房价数据集的特征数据和标签数据。
将数据集中的特征存储在X中:
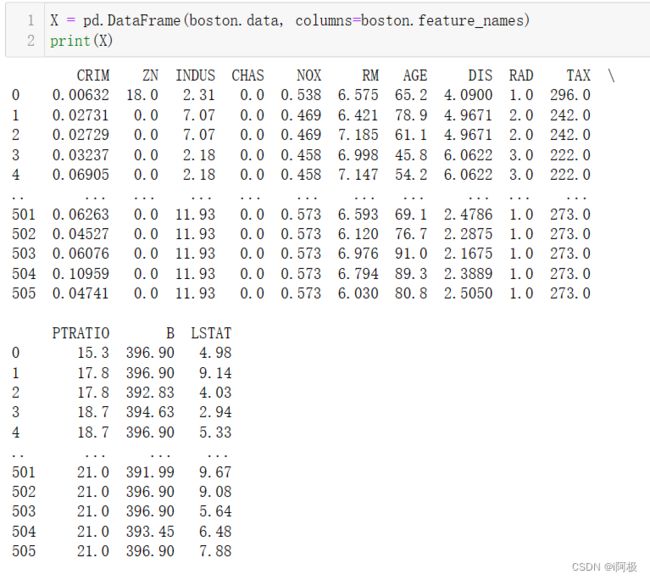
X = pd.DataFrame(boston.data, columns=boston.feature_names)
print(X)
X通过Bunch对象的data属性获取特征数据,其中data是一个二维数组,每一行代表一组数据,每一列代表一个特征。使用pandas中的DataFrame将data转换为带有列名的数据表,列名即为数据集中的特征名,存储在boston.feature_names中。
将数据集中的标签分别存储在y中:
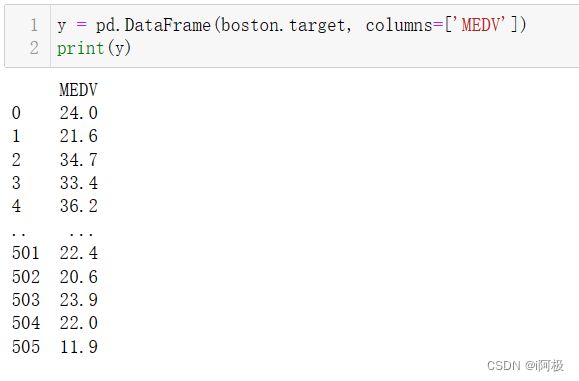
y = pd.DataFrame(boston.target, columns=['MEDV'])
print(y)
y通过Bunch对象的target属性获取标签数据,其中target是一个一维数组,每个元素代表一组数据的标签值。使用pandas中的DataFrame将target转换为带有列名的数据表,列名为’MEDV’,即为数据集中的房屋中位数价值。
2.3划分训练集和测试集
我们将使用train_test_split函数将数据集拆分为训练集和测试集。
代码如下:
from sklearn.model_selection import train_test_split
# 将数据集拆分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
train_test_split 是 scikit-learn 中一个用于划分数据集的函数,它可以将数据集划分成训练集和测试集,通常用于模型的训练和评估。
其中,参数 X 是特征数据,y 是目标变量(或标签),test_size 是测试集所占的比例,一般取 0.2 或 0.3,random_state 是随机数种子,用于保证每次划分的结果一致。
在这个例子中,train_test_split(X, y, test_size=0.2, random_state=42) 将 boston 数据集中的特征数据 X 和目标变量 y 划分为训练集和测试集,其中测试集占总数据集的 20%,随机数种子为 42。
2.4创建线性回归模型
我们将使用线性回归模型来拟合训练集。
代码如下:
from sklearn.linear_model import LinearRegression
# 创建线性回归模型
lr = LinearRegression()
# 拟合训练集
lr.fit(X_train, y_train)
2.5模型预测评价
我们已经使用线性回归模型拟合了训练集。接下来,我们可以使用predict函数来进行预测。
代码如下:
# 预测测试集
y_pred = lr.predict(X_test)
我们可以使用Scikit-learn提供的mean_squared_error函数计算预测结果的均方误差(MSE)和决定系数(R2)。
代码如下:
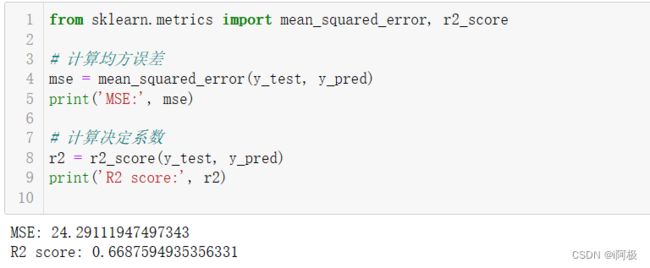
from sklearn.metrics import mean_squared_error, r2_score
# 计算均方误差
mse = mean_squared_error(y_test, y_pred)
print('MSE:', mse)
# 计算决定系数
r2 = r2_score(y_test, y_pred)
print('R2 score:', r2)
MSE是真实值与预测值之间差值的平方的平均值。它是衡量预测值与真实值之间的误差的一种方法。MSE的值越小,表示模型的预测效果越好。
R2是确定系数,用于评估模型的拟合程度。R2的值在0到1之间,越接近1表示模型的拟合程度越好。R2的值越小,表示模型对数据的解释能力越差。
在此结果中,MSE为24.2911,这意味着预测值与真实值之间的平均差值为24.2911。而R2得分为0.6688,表示模型可以解释数据的约67%的变异性,这说明模型的拟合程度还有提升的空间。
文章下方有交流学习区!一起学习进步!
首发CSDN博客,创作不易,如果觉得文章不错,可以点赞收藏评论
你的支持和鼓励是我创作的动力❗❗❗