【C++】map和set的模拟实现

---

1、map、set和红黑树源码的截取

我们红黑树的节点只需要用到value值就够了，value是什么，节点就存什么。但是，红黑树的源码为什么也要key值呢？

这是因为我们插入的时候，要用到接口bool insert（const Value& v）
但是我们查找的时候，接口iterator find(const Key& k)是通过key值来查找的，所以，红黑树源码要key值是为了查找等操作的需求

2、红黑树的迭代器

迭代器的好处是可以方便遍历，是数据结构的底层实现与用户透明。如果想要给红黑树增加迭代器，需要考虑以前问题：

begin()与end()

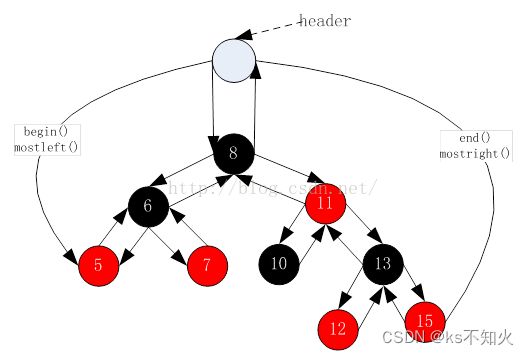
STL明确规定，begin()与end()代表的是一段前闭后开的区间，而对红黑树进行中序遍历后，可以得到一个有序的序列，因此：begin()可以放在红黑树中最小节点(即最左侧节点)的位置，end()放在最大节点(最右侧节点)的下一个位置，关键是最大节点的下一个位置在哪块？能否给成nullptr呢？答案是行不通的，因为对end()位置的迭代器进行–操作，必须要能找最后一个元素，此处就不行，因此最好的方式是将end()放在头结点的位置：

但是，上面这样过于麻烦了，我们实现的时候不需要加入header节点，正常实现即可！

3、代码部分

3-1、Set.h

#pragma once
#include "RBTree.h"

namespace bzh
{
	template<class K>
	class set
	{
		struct SetKeyofT
		{
			const K& operator()(const K& key)
			{
				return key;
			}
		};
	public:
		typedef typename RBTree<K, K, SetKeyofT>::const_iterator iterator;
		//迭代器和const迭代器底层都是const迭代器，这样一来，迭代器就不能够被更改数据了
		typedef typename RBTree<K, K, SetKeyofT>::const_iterator const_iterator;

		//模板没有实例化，编译器区分不清这里是静态变量还是类型
		//编译器不会编译类模板，只会编译实例化的类型
		//typename先告诉编译器RBTree::iterator是个类型，等模板实例化再来取
		iterator begin()const
		{
			return _t.begin();
		}
		iterator end()const
		{
			return _t.end();
		}
		pair<iterator, bool> insert(const K& key)//上面迭代器和const迭代器都是const的
		{
			//return _t.Insert(key);//这里的insert是普通迭代器
			pair<typename RBTree<K, K, SetKeyofT>::iterator, bool> ret = _t.Insert(key);
			return pair<iterator, bool>(ret.first, ret.second);
			//ret.first就是ret的迭代器，这是一个普通迭代器，这里用普通迭代器构建一个const迭代器！！！
		}
	private:
		RBTree<K, K, SetKeyofT> _t;
	};
	void test_set()
	{
		set<int> s;
		int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };
		for (const auto& e : a)
		{
			s.insert(e);
		}

		set<int>::iterator it = s.begin();
		while (it != s.end())
		{
			//*it += 10;加了const报错，不加const不报错
			cout << *it << " ";
			++it;
		}
		cout << endl;
	}
}

3-2、Map.h

#pragma once
#include "RBTree.h"

namespace bzh
{
	template<class K, class V>
	class map
	{
		struct MapKeyofT
		{
			const K& operator()(const pair<const K, V>& kv)
			{
				return kv.first;
			}
		};
	public:
		typedef typename RBTree<K, pair<const K, V>, MapKeyofT>::iterator iterator;
		typedef typename RBTree<K, pair<const K, V>, MapKeyofT>::const_iterator const_iterator;
		iterator begin()
		{
			return _t.begin();
		}
		iterator end()
		{
			return _t.end();
		}
		const_iterator begin()const
		{
			return _t.begin();
		}
		const_iterator end()const
		{
			return _t.end();
		}
		pair<iterator, bool> insert(const pair<const K, V>& kv)
		{
			return _t.Insert(kv);
		}
		V& operator[](const K& key)
		{
			pair<iterator, bool> ret = insert(make_pair(key, V()));
			return ret.first->second;
		}
	private:
		RBTree<K, pair<const K, V>, MapKeyofT> _t;//map的v可以改变，所以不加const
	};
	void test_map()
	{
		int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };
		map<int, int> m;
		for (const auto& e : a)
		{
			m.insert(make_pair(e,e));
		}
		map<int, int>::iterator it = m.begin();
		while (it != m.end())
		{
			//it->first++;
			it->second++;
			cout << it->first << " : " << it->second << " ";
			++it;
		}
		cout << endl;
	}
}

3-3、RBTee.h

#pragma once
#include
#include 
#include 
using namespace std;
enum colors
{
	RED,
	BLOCK,
};
template <class T>
class RBTreeNode
{
public:
	T _data;
	RBTreeNode<T>* _left;
	RBTreeNode<T>* _right;
	RBTreeNode<T>* _parent;

	colors _col;

	RBTreeNode(const T& data)
		:_data(data)
		, _left(nullptr)
		, _right(nullptr)
		, _parent(nullptr)
		, _col(RED)
	{}
};

template <class T, class Ref, class Ptr>
struct __RBTreeiterator
{
	typedef RBTreeNode<T> Node;
	typedef __RBTreeiterator<T, Ref, Ptr> Self;

	//T&,T*时，Self和iterator一样
	//const T&,constT*时，Self和iterator不一样！！！
	typedef __RBTreeiterator<T, T&, T*> iterator;//我们自己实现普通迭代器给给const迭代器
	// 普通迭代器的时候，他是拷贝构造
	// const迭代器的时候，他是构造，支持用普通迭代器构造const迭代器
	__RBTreeiterator(const iterator& s)
		:_node(s._node)
	{}

	Node* _node;
	__RBTreeiterator(Node* node)
		:_node(node)
	{}
	Ref operator*()
	{
		return _node->_data;
	}
	Ptr operator->()
	{
		return &_node->_data;
	}
	Self& operator++()
	{
		if (_node->_right)
		{
			Node* min = _node->_right;
			while (min->_left)
			{
				min = min->_left;
			}
			_node = min;
		}
		else
		{
			Node* cur = _node;
			Node* parent = cur->_parent;
			while (parent && cur == parent->_right)
			{
				cur = cur->_parent;
				parent = parent->_parent;
			}
			_node = parent;
		}
		return *this;
	}
	Self& operator--()
	{
		if (_node->_left)
		{
			Node* max = _node->_left;
			while (max->_right)
			{
				max = max->_right;
			}
			_node = max;
		}
		else
		{
			Node* cur = _node;
			Node* parent = cur->_parent;
			while (parent && cur == parent->_left)
			{
				cur = cur->_parent;
				parent = parent->_parent;
			}
			_node = parent;
		}
		return *this;
	}
	bool operator!=(const Self& s)const
	{
		return _node != s._node;
	}
	bool operator==(const Self& s)const
	{
		return _node == s._node;
	}
};

template <class K, class T,class KeyofT>
class RBTree
{
	typedef RBTreeNode<T> Node;
public:
	typedef __RBTreeiterator<T,T&,T*> iterator;
	typedef __RBTreeiterator<T, const T&, const T*> const_iterator;

	iterator begin()
	{
		Node* left = _root;
		while (left && left->_left)
		{
			left = left->_left;
		}
		return iterator(left);
	}
	iterator end()
	{
		return iterator(nullptr);
	}
	const_iterator begin() const
	{
		Node* left = _root;
		while (left && left->_left)
		{
			left = left->_left;
		}
		return const_iterator(left);
	}
	const_iterator end() const
	{
		return const_iterator(nullptr);
	}	
	pair<iterator,bool> Insert(const T& data)
	{
		if (_root == nullptr)
		{
			_root = new Node(data);
			_root->_col = BLOCK;
			return make_pair(iterator(_root),true);
		}
		KeyofT kot;/
		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			//这里的_data和data不能直接进行比较，如果是set可以比较
			//但是map模型不能比较，因为库里面pair的first和secnod都进行了比较。而且因为库里面写好了，我们不能写一个只比较first的函数，这就和库一样了
			//所以我们要加一个keyofvalue的模板参数，把pair里面的key取出来
			if (kot(cur->_data) > kot(data))
			{
				parent = cur;
				cur = cur->_left;
			}
			else if (kot(cur->_data) < kot(data))//我比你大，往右找
			{
				parent = cur;
				cur = cur->_right;
			}
			else
			{
				return make_pair(iterator(cur), false);//不存在找到，因为AVL树不允许有重复值
			}
		}
		走到这里就表示找到我们要插入kv值的正确位置了
		cur = new Node(data);
		Node* newnode = cur;
		cur->_col = RED;//这里插入一个节点，颜色设置为红色！！！
		//插入一个节点，设置为红色。我们就违背了红黑树规则3（红黑树的性质那里）
		//插入一个节点，设置为黑色。我们就违背了红黑树规则4
		// 
		//但是，我们可以仔细观察，发现违背规则3然后对红黑树进行修改，比违背规则4进行修改简单的多！！！
		//而且插入设置为红色不一定破环了规则3，就算违背规则3破坏的是一条路径，
		//而规则4是整棵树的全部路径。所以这里设置节点为红色比较容易控制

		if (kot(parent->_data) < kot(data))//如果new的节点比父节点大，那么父节点的右指针指向new节点
		{
			parent->_right = cur;
			cur->_parent = parent;
		}
		else//如果new的节点比父节点小，那么父节点的左指针指向new节点
		{
			parent->_left = cur;
			cur->_parent = parent;
		}
		while (parent && parent->_col == RED)//父亲颜色为黑就不需要处理了，颜色为红就要处理
		{
			Node* gf = parent->_parent;//
			if (parent == gf->_left)
			{
				Node* uncle = gf->_right;
				if (uncle && uncle->_col == RED)
				{
					parent->_col = uncle->_col = BLOCK;
					gf->_col = RED;
					cur = gf;
					parent = cur->_parent;
				}
				else
				{
					if (cur == parent->_left)
					{
						//新增cur在父亲的左，右单旋
						RotateR(gf);
						parent->_col = BLOCK;
						gf->_col = RED;
					}
					else
					{
						//情况三，双旋
						RotateL(parent);
						RotateR(gf);
						cur->_col = BLOCK;
						gf->_col = RED;
					}
					break;//这里要break，因为这一层已经处理完了，上面有问题是上面的事，与这一层无关
				}
			}
			else
			{
				Node* uncle = gf->_left;
				if (uncle && uncle->_col == RED)
				{
					parent->_col = uncle->_col = BLOCK;
					gf->_col = RED;

					cur = gf;
					parent = cur->_parent;
				}
				else
				{
					if (cur == parent->_right)
					{
						RotateL(gf);
						parent->_col = BLOCK;
						gf->_col = RED;
					}
					else
					{
						RotateR(parent);
						RotateL(gf);
						cur->_col = BLOCK;
						gf->_col = RED;
					}

					break;
				}
			}
		}
		_root->_col = BLOCK;
		return make_pair(iterator(newnode), true);
	}
	void RotateL(Node* parent)
	{
		Node* subr = parent->_right;
		Node* subrl = subr->_left;
		parent->_right = subrl;
		if (subrl)//上面的节点不可能为空，但是这里的subrl可能为空
		{
			subrl->_parent = parent;
		}
		Node* ppnode = parent->_parent;
		subr->_left = parent;
		parent->_parent = subr;
		if (ppnode == nullptr)//如果
		{
			_root = subr;
			_root->_parent = nullptr;//这里要置空
		}
		else
		{
			if (ppnode->_left == parent)
			{
				ppnode->_left = subr;
			}
			else
			{
				ppnode->_right = subr;
			}
			subr->_parent = ppnode;
		}
	}
	void RotateR(Node* parent)
	{
		Node* subl = parent->_left;
		Node* sublr = subl->_right;
		parent->_left = sublr;
		if (sublr)
		{
			sublr->_parent = parent;
		}
		Node* ppnode = parent->_parent;
		subl->_right = parent;
		parent->_parent = subl;
		if (ppnode == nullptr)
		{
			_root = subl;
			subl->_parent = nullptr;
		}
		else
		{
			if (ppnode->_left == parent)
			{
				ppnode->_left = subl;
			}
			else
			{
				ppnode->_right = subl;
			}
			subl->_parent = ppnode;
		}
	}
	void Inorder()//中序遍历
	{
		_Inorder(_root);
	}
	void _Inorder(Node* root)//中序遍历
	{
		if (root == nullptr)
		{
			return;
		}
		_Inorder(root->_left);
		cout << root->_kv.first << ":" << root->_kv.second << endl;
		_Inorder(root->_right);
	}

	bool Check(Node* root, int blackNum, const int ref)
	{
		if (root == nullptr)
		{
			//cout << blackNum << endl;
			if (blackNum != ref)
			{
				cout << "违反规则：本条路径的黑色节点的数量跟最左路径不相等" << endl;
				return false;
			}
			return true;
		}
		if (root->_col == RED && root->_parent->_col == RED)
		{
			cout << "违反规则：出现连续红色节点" << endl;
			return false;
		}
		if (root->_col == BLOCK)
		{
			++blackNum;
		}
		return Check(root->_left, blackNum, ref) && Check(root->_right, blackNum, ref);
	}
	bool IsBalance()判断是否为红黑树，这里的IsBalance不是递归函数
	{
		if (_root == nullptr)//这里不需要递归，所以就使用_root，不用传参
			return true;
		if (_root->_col != BLOCK)//这里判断的是整棵树的根，不是每一个根都要为黑，
								//所以我们要再写一个函数来处理
			return false;

		int ref = 0;
		Node* left = _root;
		while (left)
		{
			if (left->_col == BLOCK)
				++ref;
			left = left->_left;
		}
		return Check(_root, 0, ref);
	}
private:
	Node* _root = nullptr;
};

void testaaa()
{
	int a[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };
	int a[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };
	//int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };
	int a[] = { 1,2,3 };
	//RBTree q;
	//for (auto e : a)
	//{
	//	q.Insert(make_pair(e, e));
	//}

	//q.Inorder();
	//cout << q.IsBalance();

	srand(time(0));
	/*const size_t N = 10;
	RBTree t;
	for (size_t i = 0; i < N; ++i)
	{
		size_t x = rand();
		t.Insert(make_pair(x, x));
		cout << t.IsBalance() << endl;
	}
	t.Inorder();
	cout << t.IsBalance() << endl;*/
}

3-4、测试代码

#include
#include
#include
#include 
#include 
#include
using namespace std;

#include 

//int main()
//{
//	unordered_set us;
//	us.insert(3);
//	us.insert(1);
//	us.insert(3);
//	us.insert(2);
//	us.insert(0);
//
//	unordered_set::iterator it = us.begin();
//	while (it != us.end())
//	{
//		cout << *it << " ";
//		++it;
//	}
//	cout << endl;
//
//	string arr[] = { "ƻ", "", "㽶", "ݮ", "ƻ", "", "ƻ", "ƻ", "", "ƻ", "㽶", "ƻ", "㽶" };
//		
//	unordered_map countMap;
//	for (auto& e : arr)
//	{
//		//map::iterator it = countMap
//	/*	auto it = countMap.find(e);
//		if (it == countMap.end())
//		{
//			countMap.insert(make_pair(e, 1));
//		}
//		else
//		{
//			it->second++;
//		}*/
//
//		countMap[e]++;
//	}
//		
//	for (const auto& kv : countMap)
//	{
//		cout << kv.first << ":" << kv.second << endl;
//	}
//
//	return 0;
//}

//int main()
//{
//	const size_t N = 1000000;
//
//	unordered_set us;
//	set s;
//
//	vector v;
//	v.reserve(N);
//	srand(time(0));
//	for (size_t i = 0; i < N; ++i)
//	{
//		//v.push_back(rand());
//		//v.push_back(rand()+i);
//		v.push_back(i);
//	}
//
//	size_t begin1 = clock();
//	for (auto e : v)
//	{
//		s.insert(e);
//	}
//	size_t end1 = clock();
//	cout << "set insert:" << end1 - begin1 << endl;
//
//	size_t begin2 = clock();
//	for (auto e : v)
//	{
//		us.insert(e);
//	}
//	size_t end2 = clock();
//	cout << "unordered_set insert:" << end2 - begin2 << endl;
//
//
//	size_t begin3 = clock();
//	for (auto e : v)
//	{
//		s.find(e);
//	}
//	size_t end3 = clock();
//	cout << "set find:" << end3 - begin3 << endl;
//
//	size_t begin4 = clock();
//	for (auto e : v)
//	{
//		us.find(e);
//	}
//	size_t end4 = clock();
//	cout << "unordered_set find:" << end4 - begin4 << endl;
//
//	cout << s.size() << endl;
//	cout << us.size() << endl;
//
//	size_t begin5 = clock();
//	for (auto e : v)
//	{
//		s.erase(e);
//	}
//	size_t end5 = clock();
//	cout << "set erase:" << end5 - begin5 << endl;
//
//	size_t begin6 = clock();
//	for (auto e : v)
//	{
//		us.erase(e);
//	}
//	size_t end6 = clock();
//	cout << "unordered_set erase:" << end6 - begin6 << endl;
//	
//	return 0;
//}

int main()
{
	return 0;
}