用Keras单层网络预测银行客户流失率

用Keras单层网络预测银行客户流失率

描述

已知一批客户数据，来预测某个银行的客户是否流失。通过学习历史数据，如果机器能判断出哪些客户很有可能在未来两年内结束在银行的业务（这当然是银行所不希望看到的），那么银行就可以采取相应的、有针对性的措施来挽留这些高流失风险的客户，本质上都是分类，我们看看神经网络来解决这类问题有何优势。

源码下载

目标

• 熟练掌握数据的处理和分析

• 理解神经网络的原理

• 使用Keras构建单层神经网络

• 如何解决数据不均衡问题

环境

• 操作系统：Windows10、Ubuntu18.04

• 工具软件：Anaconda3 2019、Python3.7

• 硬件环境：无特殊要求

• 依赖库列表

  numpy                     1.19.5
  pandas                    1.1.5
  ipython                   7.16.3
  keras 					  2.6.0
  

分析

1、数据的准备与分析

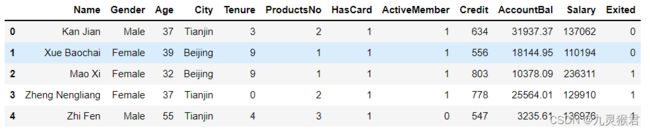
打开BankCustomer.csv 数据文件，观察数据集，我们发现里面中主要是客户的个人资料以及在该银行的历史交易信息，包括：

• Name : 客户姓名

• Gender: 性别

• Age: 年龄

• City：城市

• Tenure:已经成为客户的年头

• Products No：拥有的产品数量

• Has Card: 是否有信用卡

• Active Member:是否为活跃用户

• Credit:信用评级

• Account Bai: 银行存款余额

这些信息对于客户是否会流失是具有指向性的。

数据清洗工作

对这个数据集，我们主要做了以下3个方面的清洗工作。

1. 性别：是二元类型，转换为0/1格式（机器学习中的文本格式数据都要转换为数字代码）

2. 城市：多元类别类型，应转换为二元类别哑变量

3. 姓名：对于客户流失与否的预测完全不相关，直接忽略

2、数据的分布

观察右下角的客户是否已流失图，也就是y值的分布图，10000个客户里，大概是8000个客户，也就是80%左右的客户没有离开，只有20%的客户流失。也就是说标签的类别分布是不均衡的。就是这个80%：20%的比例来说，如果预测是80%以下的准确率等于机器什么也没做。 我们的神经网络算法预测结果一定会受到影响。

3、使用Keras构建单层神经网络

本任务中我们使用kears构建了一个单层神经网络，该网络中有3个神经元。

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Veo8nM7U-1681438382000)(image/image-20220428144724808.png)]

方法和参数说明

• 序贯(sequential)模型,也叫顺序模型，是最常用的深度网络层和层间的架构，也就是有一个层接着一个层，顺序的堆叠

• 密集（dense）层：是最常用的深度网络层的类型，也称为全连接层，既当前层和其下一层的所有神经元之间全有连接

• Summary方法 先了神经网络的结构，包括每个层的类型、输出张量的形状、参数数量及整个网络的参数数量。这个网络只有3个层，493个参数（就是每个神经元的权重），这对于神经网络来说，参数数量已经非常少了。

方法和参数说明

• 模型的创建：ann=Sequential() 创建了一个序贯神经网络模型

• 第一层输入层：通过add方法，一层层的顺序增加层结构

• Dense是层的类型，代表密集层网络，是神经网络中最基本的层，也叫全连接层，后期还会看到CNN中的Conv2D层，RNN中的LSTM层…解决回归、分类等普通机器学习问题，用全连接层就可以了。

• Input_dim:是输入维度，输入维度必须与特征维度相同。这里指定的网络能接收的输入维度为11

• Unit/output_dim：是输出维度：设置为12，12这个值目前是随意选择的。其实也就是神经元的格式，维度越大，则模型覆盖面也也大，但模型也越复杂，计算量也多。对于简单问题12维是一个合适的数字，太多容易过拟合，太少（不能少于特征维度）则拟合能力不够。

• Activation是激活函数：是每一层都需要设置的参数。这里激活函数选择的是relu。

4、混淆矩阵、精确率、召回率和F1分数

假设有一个手机生产厂商，每天生产手机1 000 部。某天生产的手机中，出现了2个劣质品。目前通过机器学习来分析数据特征（如手机质量、形状规格等），鉴定劣质品样本。其中数据集真值和机器学习模型的合格品和劣质品个数如下表所示：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-w3FhGT2f-1681438382002)(image/image-20220428153007575.png)]

表中机器学习模型的预测结果显示合格品999个，劣质品1个，其准确率为99.9%，理论上相当高了。

然而从我们的目标来说，这个模型实际上是失败了。一共2个劣质品，只发现1个，有50%正样品没有测准。

为了评估这种数据集，引入一个测试值与真值组成的矩阵：

2个劣质产品，有一个误判，这个被标为假负

998个合格品被检测，也没有劣质品被误判为合格品，因此有998个真负，0个假正

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-l9rW27fQ-1681438382004)(image/image-20220428153515728.png)]

Tips: 是否为劣质产品 0 False/负 1 True/正

• 表中机器学习模型的预测结果显示合格品999个，劣质品1个，其准确率为99.9%，理论上相当高了

• 然而从我们的目标来说，这个模型实际上是失败了。一共2个劣质品，只发现1个，有50%正样品（劣质品既标签值为1的阳性正样品）没有测准。

• 模型的好于不好，是基于用什么标准衡量。

• 对于这种正样品本和负样本极度不平衡的样本集，我们需要引进新的评估指标

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-AM2jLcFL-1681438382006)(image/image-20220428153030671.png)]

Tips: 类别样本比例 80%:20%

上面这种矩阵，在机器学习中也是一种对模型的可视化评估工具，在监督学习中叫作混淆矩阵（confusion matrix）,如下图所示：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-iZEbMM8R-1681438382009)(image/image-20220428153539008.png)]

从这个混淆矩阵出发，又形成一些新的评估指标：

①精确率（查准率）

②召回率（查全率）

③F1分数 （把精确率和召回率结合起来，就得到F1分数）

本例精确率（Precision）：1/(1+0)=100%

预测为真的真样品 除以 （预测为真的真样品 与 预测为假的真样品的和）

本例召回率(Recall)：1/（1+1）=50%

就是需要考虑被误判为合格的劣质品：

劣质品蒙混过了质检，跑出厂了，得“召回”，销毁掉。

预测为真的假样品/(预测为真的加样品+预测为假的假样品)

F1分数： 33.3%

可以同时体现上面两个评估效果的标准，数学上定义为精确率和召回率的调和均值，也是在评估这类样本分类数据不平衡的问题时，所着重看重的标准

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-9ZqxwM6X-1681438382011)(image/image-20220428153649422.png)]

5、特征缩放

神经网络不喜欢大的取值范围，因此需要将输入神经网络的数据标准化，把数据约束在较小的区间，这样可消除离群样本对函数形状的影响。

数值过大的数据以及离群样本的存在（如下图）会使函数曲线变的奇形怪状，从而影响梯度下降过程中的收敛。而特征缩放，将极大的提高梯度下降的效率

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-V6Yf7Eun-1681438382013)(image/image-20220428155339648.png)]

特征缩放有很多形式，这里对数据进行标准化，其步骤：对输入的数据的每个特征（也就是输入数据矩阵中的一整列）减去特征平均值，再除以标准差，之后得到的特征平均值为0，标准差为1。

公式如下：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-3zfvobyp-1681438382016)(image/image-20220428155717870.png)]

手动实现代码如下：

# mean = X_train.mean(axis=0) # 计算训练集均值
# X_train -= mean # 训练集减去训练集均值
# std = X_train.std(axis=0) # 计算训练集方差
# X_train /= std # 训练集除以训练集标准差
# X_test -= mean # 测试集减去训练集均值
# X_test /= std # 测试集减去训练集均值

调用Sklearn标准化工具进行特征缩放

from sklearn.preprocessing import StandardScaler # 导入特征缩放器
sc = StandardScaler() # 特征缩放器
X_train = sc.fit_transform(X_train) # 拟合并应用于训练集
X_test = sc.transform (X_test) # 训练集结果应用于测试集

缩放后的数据集特征值区间显著减小如下图：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-nbDpCytD-1681438382018)(image/image-20220428155403221.png)]

实施

1、读取文件

import numpy as np #导入NumPy数学工具箱
import pandas as pd #导入Pandas数据处理工具箱
df_bank = pd.read_csv("../dataset/BankCustomer.csv") # 读取文件
df_bank.head() # 显示文件前5行

输出前5行数据如下图：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-VAoDxSd0-1681438382021)(image/image-20220428144151495.png)]

2、显示数据的分布情况

import matplotlib.pyplot as plt #导入matplotlib画图工具箱
import seaborn as sns #导入seaborn画图工具箱
# 显示不同特征的分布情况
features=[ 'City', 'Gender','Age','Tenure', 
           'ProductsNo', 'HasCard', 'ActiveMember', 'Exited']
fig=plt.subplots(figsize=(15,15))
for i, j in enumerate(features):
    plt.subplot(4, 2, i+1)
    plt.subplots_adjust(hspace = 1.0)
    sns.countplot(x=j,data = df_bank)
    plt.title("No. of costumers")

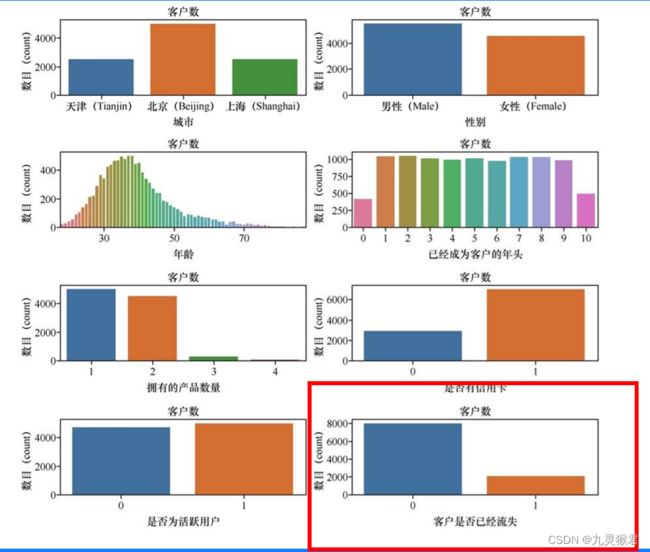
输出的数据分布情况如下图:

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-xTOOdqxB-1681438382023)(image/image-20220428144517566.png)]

从图中大概看得出，北京的客户最多，男女客户比例大致一直，年龄和客户数量呈现正态分布（钟形曲线，中间高两边低）。

这个数据集有个显著特点：也就是说标签的类别分布是不均衡的。就是这个80%：20%的比例来说，如果预测是80%以下的准确率等于机器什么也没做。 我们的神经网络算法预测结果一定会受到影响。

3、数据整理工作

对这个数据集，我们主要做了以下3个方面的清洗工作。

1. 性别：是二元类型，转换为0/1格式（机器学习中的文本格式数据都要转换为数字代码）

2. 城市：多元类别类型，应转换为二元类别哑变量

3. 姓名：对于客户流失与否的预测完全不相关，直接忽略

# 把二元类别文本数字化
df_bank['Gender'].replace("Female",0,inplace = True)
df_bank['Gender'].replace("Male",1,inplace=True)
# 显示数字类别
print("Gender unique values",df_bank['Gender'].unique())
# 把多元类别转换成多个二元哑变量，然后贴回原始数据集
d_city = pd.get_dummies(df_bank['City'], prefix = "City")
df_bank = [df_bank, d_city]
df_bank = pd.concat(df_bank, axis = 1)
# 构建特征和标签集合
y = df_bank ['Exited']
X = df_bank.drop(['Name', 'Exited','City'], axis=1)
X.head() #显示新的特征集

输出的清理之后的数据集如下图所示：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-XbiVvVNM-1681438382025)(image/image-20220428145908041.png)]

此时新数据集的特征数目是12个，既特征维度是12。

然后用标准方法拆分数据集为测试和训练集

from sklearn.model_selection import train_test_split #拆分数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, 
                                   test_size=0.2, random_state=0)

4、先尝试逻辑回归算法

from sklearn.linear_model import LogisticRegression # 导入Sklearn模型
lr = LogisticRegression() # 逻辑回归模型
history = lr.fit(X_train,y_train) # 训练机器
print("逻辑回归测试集准确率 {:.2f}%".format(lr.score(X_test,y_test)*100))

输出结果如下：

逻辑回归测试集准确率 78.35%

结果显示预测准确率为78.3%。作为分类问题，这个准确率表面上看还可以，比盲目猜测强很多，我们可以把它看做一个评估基准，看看采用神经网络的算法进行机器学习后，准确率会不会有所提升。

5、单隐层神经网络的Keras实现

import keras # 导入Keras库
from keras.models import Sequential # 导入Keras序贯模型
from keras.layers import Dense # 导入Keras密集连接层
ann = Sequential() # 创建一个序贯ANN(Artifical Neural Network)模型
ann.add(Dense(units=12, input_dim=12, activation = 'relu')) # 添加输入层
ann.add(Dense(units=24, activation = 'relu')) # 添加隐层
ann.add(Dense(units=1, activation = 'sigmoid')) # 添加输出层
ann.summary() # 显示网络模型(这个语句不是必须的)

运行上面的代码后，将输出神经网络的结构信息：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-lbHbTVQs-1681438382026)(image/image-20220428150343790.png)]

summary方法显示了神经网络的结构，包括每个层的类型、输出张量形状、参数数量以及整个网络的参数数量。这个网络只有3层，493个参数（就是每个神经元的权重等），这对于神经网络来说，参数数量已经算是很少了。

6、训练单层神经网络

下面开始训练刚才编译好的神经网络，和其他传统机器学习算法一样，神经网络的拟合过程也是通过fit方法实现的。在此通过history变量把训练过程中的信息保存下俩，留待以后分析：

# 编译神经网络，指定优化器，损失函数，以及评估标准
ann.compile(optimizer = 'adam',           #优化器
            loss = 'binary_crossentropy', #损失函数  
            metrics = ['acc'])       #评估指标
history = ann.fit(X_train, y_train, # 指定训练集
                  epochs=30,        # 指定训练的轮次
                  batch_size=64,    # 指定数据批量
                  validation_data=(X_test, y_test)) #指定验证集,这里为了简化模型，直接用测试集数据进行验证

运行fit方法后，神经网络的训练就开始了，接着开始逐步输出每个轮次的训练集准确率和验证集准确率，结果如下：

Epoch 1/30
125/125 [==============================] - 1s 3ms/step - loss: 175.5270 - acc: 0.6825 - val_loss: 32.4774 - val_acc: 0.4655
Epoch 2/30
125/125 [==============================] - 0s 2ms/step - loss: 49.2496 - acc: 0.6806 - val_loss: 29.8218 - val_acc: 0.4665
Epoch 3/30
125/125 [==============================] - 0s 2ms/step - loss: 30.4199 - acc: 0.6775 - val_loss: 14.5191 - val_acc: 0.7895
Epoch 4/30
125/125 [==============================] - 0s 2ms/step - loss: 27.5663 - acc: 0.6795 - val_loss: 11.6139 - val_acc: 0.7485
Epoch 5/30
125/125 [==============================] - 0s 2ms/step - loss: 28.2143 - acc: 0.6764 - val_loss: 6.5864 - val_acc: 0.7830
Epoch 6/30
125/125 [==============================] - 0s 2ms/step - loss: 27.3185 - acc: 0.6884 - val_loss: 22.8819 - val_acc: 0.7900
Epoch 7/30
125/125 [==============================] - 0s 2ms/step - loss: 36.3250 - acc: 0.6913 - val_loss: 15.9079 - val_acc: 0.4690
Epoch 8/30
125/125 [==============================] - 0s 2ms/step - loss: 27.6163 - acc: 0.6834 - val_loss: 49.1711 - val_acc: 0.7910
Epoch 9/30
125/125 [==============================] - 0s 2ms/step - loss: 27.9164 - acc: 0.6743 - val_loss: 6.4183 - val_acc: 0.7730
Epoch 10/30
125/125 [==============================] - 0s 2ms/step - loss: 22.3592 - acc: 0.6824 - val_loss: 33.6894 - val_acc: 0.7880
Epoch 11/30
125/125 [==============================] - 0s 2ms/step - loss: 23.7578 - acc: 0.6939 - val_loss: 28.8664 - val_acc: 0.4315
Epoch 12/30
125/125 [==============================] - 0s 2ms/step - loss: 31.0487 - acc: 0.6841 - val_loss: 8.2716 - val_acc: 0.7895
Epoch 13/30
125/125 [==============================] - 0s 2ms/step - loss: 48.6107 - acc: 0.6881 - val_loss: 25.5391 - val_acc: 0.7820
Epoch 14/30
125/125 [==============================] - 0s 2ms/step - loss: 21.9583 - acc: 0.6875 - val_loss: 22.1150 - val_acc: 0.7875
Epoch 15/30
125/125 [==============================] - 0s 2ms/step - loss: 33.7498 - acc: 0.6806 - val_loss: 6.8649 - val_acc: 0.7825
Epoch 16/30
125/125 [==============================] - 0s 2ms/step - loss: 31.3620 - acc: 0.6901 - val_loss: 14.3301 - val_acc: 0.7910
Epoch 17/30
125/125 [==============================] - 0s 3ms/step - loss: 36.7263 - acc: 0.6840 - val_loss: 32.0003 - val_acc: 0.7900
Epoch 18/30
125/125 [==============================] - 0s 3ms/step - loss: 25.7709 - acc: 0.6917 - val_loss: 10.3033 - val_acc: 0.7875
Epoch 19/30
125/125 [==============================] - 0s 2ms/step - loss: 45.1768 - acc: 0.6819 - val_loss: 28.6102 - val_acc: 0.4700
Epoch 20/30
125/125 [==============================] - 0s 2ms/step - loss: 21.3710 - acc: 0.6965 - val_loss: 23.3337 - val_acc: 0.7845
Epoch 21/30
125/125 [==============================] - 0s 2ms/step - loss: 26.6743 - acc: 0.6808 - val_loss: 28.7952 - val_acc: 0.7895
Epoch 22/30
125/125 [==============================] - 0s 2ms/step - loss: 25.5405 - acc: 0.6854 - val_loss: 23.5309 - val_acc: 0.7895
Epoch 23/30
125/125 [==============================] - 0s 2ms/step - loss: 21.9671 - acc: 0.6842 - val_loss: 31.2261 - val_acc: 0.7900
Epoch 24/30
125/125 [==============================] - 0s 2ms/step - loss: 27.1473 - acc: 0.6811 - val_loss: 10.6314 - val_acc: 0.7905
Epoch 25/30
125/125 [==============================] - 0s 2ms/step - loss: 23.7522 - acc: 0.6769 - val_loss: 36.7612 - val_acc: 0.7870
Epoch 26/30
125/125 [==============================] - 0s 2ms/step - loss: 25.1490 - acc: 0.6802 - val_loss: 35.8863 - val_acc: 0.2455
Epoch 27/30
125/125 [==============================] - 0s 2ms/step - loss: 25.1648 - acc: 0.6938 - val_loss: 5.9341 - val_acc: 0.5795
Epoch 28/30
125/125 [==============================] - 0s 2ms/step - loss: 30.6756 - acc: 0.6919 - val_loss: 103.0329 - val_acc: 0.4565
Epoch 29/30
125/125 [==============================] - 0s 2ms/step - loss: 35.5936 - acc: 0.6731 - val_loss: 91.7984 - val_acc: 0.7905
Epoch 30/30
125/125 [==============================] - 0s 2ms/step - loss: 36.2248 - acc: 0.6945 - val_loss: 35.3865 - val_acc: 0.7890

7、训练过程的图像化显示

训练过程中输出的信息包括每轮训练的损失值、准确率等。但是这个输出信息有30轮数据，很冗长，看起来特别费劲。可以用下面代码定义一个函数，显示基于训练集和验证集的损失曲线，以及准确率随迭代次数变化的曲线。

def show_history(history): # 显示训练过程中的学习曲线
    loss = history.history['loss']
    val_loss = history.history['val_loss']
    epochs = range(1, len(loss) + 1)
    plt.figure(figsize=(12,4))
    plt.subplot(1, 2, 1)
    plt.plot(epochs, loss, 'bo', label='Training loss')
    plt.plot(epochs, val_loss, 'b', label='Validation loss')
    plt.title('Training and validation loss')
    plt.xlabel('Epochs')
    plt.ylabel('Loss')
    plt.legend()
    acc = history.history['acc']
    val_acc = history.history['val_acc']
    plt.subplot(1, 2, 2)
    plt.plot(epochs, acc, 'bo', label='Training acc')
    plt.plot(epochs, val_acc, 'b', label='Validation acc')
    plt.title('Training and validation accuracy')
    plt.xlabel('Epochs')
    plt.ylabel('Accuracy')
    plt.legend()
    plt.show()
show_history(history) # 调用这个函数，并将神经网络训练历史数据作为参数输入

这种图像化的显示看起来就清晰多了，如下图（图中准确率均以小数形式表示，实验指导书中以百分数形式表示）

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-7oJcBZU7-1681438382030)(image/image-20220428152657536.png)]

8、解决分类数据不平衡问题

y_pred = ann.predict(X_test,batch_size=10) # 预测测试集的标签
y_pred = np.round(y_pred) # 四舍五入，将分类概率值转换成0/1整数值
from sklearn.metrics import classification_report # 导入分类报告
def show_report(X_test, y_test, y_pred): # 定义一个函数显示分类报告
    if y_test.shape != (2000,1):
        y_test = y_test.values # 把Panda series转换成Numpy array
        y_test = y_test.reshape((len(y_test),1)) # 转换成与y_pred相同的形状 
    print(classification_report(y_test,y_pred,labels=[0, 1])) #调用分类报告   
    from sklearn.metrics import confusion_matrix # 导入混淆矩阵
def show_matrix(y_test, y_pred): # 定义一个函数显示混淆矩阵
    cm = confusion_matrix(y_test,y_pred) # 调用混淆矩阵
    plt.title("ANN Confusion Matrix") # 标题
    sns.heatmap(cm,annot=True,cmap="Blues",fmt="d",cbar=False) # 热力图设定
    plt.show() # 显示混淆矩阵


show_report(X_test, y_test, y_pred) # 调用函数显示分类报告
show_matrix(y_test, y_pred) # 调用函数显示混淆矩阵

分类和混淆矩阵如下：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-VzwwrXC7-1681438382032)(image/image-20220428155104628.png)]

9、特征缩放

from sklearn.preprocessing import StandardScaler # 导入特征缩放器
sc = StandardScaler() # 特征缩放器
X_train = sc.fit_transform(X_train) # 拟合并应用于训练集
X_test = sc.transform (X_test) # 训练集结果应用于测试集

10、特征缩放后，重新运行相同的逻辑回归和单层神经网络

逻辑回归

history = ann.fit(X_train, y_train, # 指定训练集
                  epochs=30,        # 指定训练的轮次
                  batch_size=64,    # 指定数据批量
                  validation_data=(X_test, y_test)) #指定验证集
y_pred = ann.predict(X_test,batch_size=10) # 预测测试集的标签
y_pred = np.round(y_pred) # 将分类概率值转换成0/1整数值

输出结果：

逻辑回归测试集准确率 80.50%

单层神经网络

history = ann.fit(X_train, y_train, # 指定训练集
                  epochs=30,        # 指定训练的轮次
                  batch_size=64,    # 指定数据批量
                  validation_data=(X_test, y_test)) #指定验证集
y_pred = ann.predict(X_test,batch_size=10) # 预测测试集的标签
y_pred = np.round(y_pred) # 将分类概率值转换成0/1整数值

输出结果：

Epoch 1/30
125/125 [==============================] - 1s 4ms/step - loss: 0.4966 - acc: 0.7950 - val_loss: 0.4465 - val_acc: 0.8030
Epoch 2/30
125/125 [==============================] - 0s 3ms/step - loss: 0.4330 - acc: 0.8100 - val_loss: 0.4296 - val_acc: 0.8155
Epoch 3/30
125/125 [==============================] - 0s 3ms/step - loss: 0.4205 - acc: 0.8174 - val_loss: 0.4234 - val_acc: 0.8200
Epoch 4/30
125/125 [==============================] - 0s 3ms/step - loss: 0.4138 - acc: 0.8224 - val_loss: 0.4191 - val_acc: 0.8250
Epoch 5/30
125/125 [==============================] - 0s 3ms/step - loss: 0.4097 - acc: 0.8250 - val_loss: 0.4156 - val_acc: 0.8295
Epoch 6/30
125/125 [==============================] - 0s 3ms/step - loss: 0.4055 - acc: 0.8275 - val_loss: 0.4123 - val_acc: 0.8290
Epoch 7/30
125/125 [==============================] - 0s 3ms/step - loss: 0.4013 - acc: 0.8301 - val_loss: 0.4086 - val_acc: 0.8290
Epoch 8/30
125/125 [==============================] - 0s 3ms/step - loss: 0.3969 - acc: 0.8340 - val_loss: 0.4047 - val_acc: 0.8320
Epoch 9/30
125/125 [==============================] - 0s 3ms/step - loss: 0.3921 - acc: 0.8347 - val_loss: 0.3998 - val_acc: 0.8310
Epoch 10/30
125/125 [==============================] - 0s 3ms/step - loss: 0.3872 - acc: 0.8385 - val_loss: 0.3947 - val_acc: 0.8365
Epoch 11/30
125/125 [==============================] - 0s 3ms/step - loss: 0.3816 - acc: 0.8401 - val_loss: 0.3899 - val_acc: 0.8400
Epoch 12/30
125/125 [==============================] - 0s 3ms/step - loss: 0.3761 - acc: 0.8430 - val_loss: 0.3851 - val_acc: 0.8440
Epoch 13/30
125/125 [==============================] - 0s 3ms/step - loss: 0.3702 - acc: 0.8461 - val_loss: 0.3794 - val_acc: 0.8430
Epoch 14/30
125/125 [==============================] - 0s 3ms/step - loss: 0.3649 - acc: 0.8482 - val_loss: 0.3755 - val_acc: 0.8475
Epoch 15/30
125/125 [==============================] - 0s 3ms/step - loss: 0.3606 - acc: 0.8509 - val_loss: 0.3708 - val_acc: 0.8510
Epoch 16/30
125/125 [==============================] - 0s 3ms/step - loss: 0.3567 - acc: 0.8535 - val_loss: 0.3693 - val_acc: 0.8485
Epoch 17/30
125/125 [==============================] - 0s 3ms/step - loss: 0.3537 - acc: 0.8547 - val_loss: 0.3665 - val_acc: 0.8485
Epoch 18/30
125/125 [==============================] - 0s 3ms/step - loss: 0.3510 - acc: 0.8555 - val_loss: 0.3631 - val_acc: 0.8505
Epoch 19/30
125/125 [==============================] - 0s 3ms/step - loss: 0.3490 - acc: 0.8577 - val_loss: 0.3615 - val_acc: 0.8505
Epoch 20/30
125/125 [==============================] - 0s 3ms/step - loss: 0.3473 - acc: 0.8569 - val_loss: 0.3614 - val_acc: 0.8520
Epoch 21/30
125/125 [==============================] - 0s 3ms/step - loss: 0.3461 - acc: 0.8574 - val_loss: 0.3589 - val_acc: 0.8535
Epoch 22/30
125/125 [==============================] - 0s 3ms/step - loss: 0.3450 - acc: 0.8585 - val_loss: 0.3588 - val_acc: 0.8510
Epoch 23/30
125/125 [==============================] - 0s 3ms/step - loss: 0.3443 - acc: 0.8591 - val_loss: 0.3577 - val_acc: 0.8525
Epoch 24/30
125/125 [==============================] - 0s 3ms/step - loss: 0.3432 - acc: 0.8587 - val_loss: 0.3573 - val_acc: 0.8530
Epoch 25/30
125/125 [==============================] - 0s 3ms/step - loss: 0.3425 - acc: 0.8599 - val_loss: 0.3562 - val_acc: 0.8530
Epoch 26/30
125/125 [==============================] - 0s 3ms/step - loss: 0.3419 - acc: 0.8595 - val_loss: 0.3559 - val_acc: 0.8565
Epoch 27/30
125/125 [==============================] - 0s 3ms/step - loss: 0.3413 - acc: 0.8590 - val_loss: 0.3560 - val_acc: 0.8545
Epoch 28/30
125/125 [==============================] - 0s 3ms/step - loss: 0.3408 - acc: 0.8606 - val_loss: 0.3552 - val_acc: 0.8555
Epoch 29/30
125/125 [==============================] - 0s 3ms/step - loss: 0.3404 - acc: 0.8609 - val_loss: 0.3547 - val_acc: 0.8530
Epoch 30/30
125/125 [==============================] - 0s 3ms/step - loss: 0.3399 - acc: 0.8608 - val_loss: 0.3548 - val_acc: 0.8560

• 首先逻辑回归模型准确率提升至80.5%，仍然不能令我们满意。看来逻辑回归模型对于本案例不大好使。
• 而重新训练刚才的单层神经网络后，预测准确率就升至86%，这比逻辑回归模型的高出不少，此时，神经网络的效率才开始得以体现。

显示损失曲线和准确率曲线：

show_history(history)

输出结果：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-gughh512-1681438382034)(image/image-20220428160545060.png)]

发现特征缩放后，曲线也变的比较平滑。

特征缩放后，再显示分类报告和混淆矩阵

# 特征缩放后，再显示分类报告和混淆矩阵
show_report(X_test, y_test, y_pred)
show_matrix(y_test, y_pred)

输出结果:

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-QYoojevi-1681438382037)(image/image-20220428160849327.png)]

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-ApCGBjXL-1681438382040)(image/image-20220428160842201.png)]

更为重要的准确率、召回率和F1分数也大幅提升，尤其我们关注的阳性正样本类别(标签为1) 所对应的F1分数达到了50%多，虽依然不完美，比起原来0值是一个飞跃。我们可以尝试更深层的神经网络看是否能 提高这个分数

混淆矩阵显示：目前大约190多个即将流失的客户被贴上“阳性”的标签，那么银行的工作人员可以采取一些相应的措施，去挽留他们。然而，400多人中，还有219个注定要离开的客户没有被预测出来，因此模型还有进步的空间。
使。

• 而重新训练刚才的单层神经网络后，预测准确率就升至86%，这比逻辑回归模型的高出不少，此时，神经网络的效率才开始得以体现。

显示损失曲线和准确率曲线：

show_history(history)

输出结果：

[外链图片转存中…(img-gughh512-1681438382034)]

发现特征缩放后，曲线也变的比较平滑。

特征缩放后，再显示分类报告和混淆矩阵

# 特征缩放后，再显示分类报告和混淆矩阵
show_report(X_test, y_test, y_pred)
show_matrix(y_test, y_pred)

输出结果:

[外链图片转存中…(img-QYoojevi-1681438382037)]

[外链图片转存中…(img-ApCGBjXL-1681438382040)]

更为重要的准确率、召回率和F1分数也大幅提升，尤其我们关注的阳性正样本类别(标签为1) 所对应的F1分数达到了50%多，虽依然不完美，比起原来0值是一个飞跃。我们可以尝试更深层的神经网络看是否能 提高这个分数

混淆矩阵显示：目前大约190多个即将流失的客户被贴上“阳性”的标签，那么银行的工作人员可以采取一些相应的措施，去挽留他们。然而，400多人中，还有219个注定要离开的客户没有被预测出来，因此模型还有进步的空间。