sklearn中的SVM

SVM真的是很复杂的算法，原本以为原理看懂了实现就会很简单，然而事实并不是这样
sklearn中对于支持向量机提供了很多模型：LinearSVC, LinearSVR, NuSVC, NuSVR, SVC, SVR

参数

SVC

用于分类，用libsvm实现，参数如下：

• C : 惩罚项，默认为1.0，C越大容错空间越小；C越小，容错空间越大
• kernel : 核函数的类型，可选参数为：
  • “linear” : 线性核函数
  • “poly” : 多项式核函数
  • “rbf” : 高斯核函数
  • “sigmod” : sigmod核函数（竟然还有这种核函数)
  • “precomputed” : 核矩阵，表示自己提前计算好核函数矩阵
• degree : 多项式核函数的阶，默认为3，只对多项式核函数生效，其他的自动忽略
• gamma : 核函数系数，可选，float类型，默认为auto。只对’rbf’ ,’poly’ ,’sigmod’有效。如果gamma为auto，代表其值为样本特征数的倒数，即1/n_features（不是很懂）
• coef0 ：核函数中的独立项，float类型，可选，默认为0.0。只有对’poly’ 和,’sigmod’核函数有用，是指其中的参数c
• probability : probability：是否启用概率估计，bool类型，可选参数，默认为False，这必须在调用fit()之前启用，并且会fit()方法速度变慢（也不是很懂）
• tol ：svm停止训练的误差精度，float类型，可选参数，默认为1e^-3
• cache_size ：内存大小，float，可选，默认200。指定训练所需要的内存，单位MB
• class_weight：类别权重，dict类型或str类型，可选，默认None。给每个类别分别设置不同的惩罚参数C，如果没有，则会给所有类别都给C=1，即前面指出的C。如果给定参数’balance’，则使用y的值自动调整与输入数据中的类频率成反比的权重（似乎跟多分类有关）
• max_iter：最大迭代次数，int类型，默认为-1，不限制
• decision_function_shape ：决策函数类型，可选参数’ovo’和’ovr’，默认为’ovr’。’ovo’表示one vs one，’ovr’表示one vs rest。（多分类）
• random_state ：数据洗牌时的种子值，int类型，可选，默认为None

模型训练结束后，可以使用下列参数：

• support_ : array类型，支持向量的索引
• support_vectors_: 支持向量的集合
• n_support_ : 比如SVC将数据集分成了4类，该属性表示了每一类的支持向量的个数。
• dual_coef_ : array, shape = [n_class-1, n_SV] 对偶系数，支持向量在决策函数中的系数，在多分类问题中，这个会有所不同。
• coef_ : array，该参数仅在线性核时才有效，指的是每一个属性被分配的权值。
• intercept_ :array, shape = [n_class * (n_class-1) / 2]决策函数中的常数项bias。和coef_共同构成决策函数的参数值（偏置？）

LinearSVC

LinearSVC（Linear Support Vector Classification）线性支持向量机，核函数是 linear，不是基于libsvm实现的
参数：

• C：目标函数的惩罚系数C，默认C = 1.0；
• loss：指定损失函数. squared_hinge(默认), squared_hinge
• penalty ： 惩罚方式，str类型，l1, l2
• dual ：选择算法来解决对偶或原始优化问题。当nsamples>nfeatures时dual=false
• tol ：svm结束标准的精度， 默认是 1e - 3
• multi_class：如果y输出类别包含多类，用来确定多类策略， ovr表示一对多，“crammer_singer”优化所有类别的一个共同的目标 。如果选择“crammer_singer”，损失、惩罚和优化将会被被忽略。
• max_iter : 要运行的最大迭代次数。int，默认1000

线性SVM（LinearSVC)

根据前面的参数，线性SVM有两种方式实现

• LinearSVC(C)
• SVC(C=1, kernel="linear"

使用鸢尾花数据的前两列，方便画图

iris = datasets.load_iris()

data = iris.data
target = iris.target

X = X[y<2, :2]    # 只取前两列
y = y[y<2]        # 只取前两类

plt.scatter(X[y==0,0], X[y==0, 1], color="red")    # 所有0类的点，用红色
plt.scatter(X[y==1,0], X[y==1, 1], color="blue")   # 所有1类的点，用蓝色

归一化处理：

# 对X进行归一化处理
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X)
X_stand = scaler.transform(X)

使用LinearSVC分类

from sklearn.svm import LinearSVC
linearsvc = LinearSVC(C=1e9)
linearsvc.fit(X_stand, y)

# LinearSVC(C=1000000000.0, class_weight=None, dual=True, fit_intercept=True,
#           intercept_scaling=1, loss='squared_hinge', max_iter=1000,
#           multi_class='ovr', penalty='l2', random_state=None, tol=0.0001,
#           verbose=0)

结果如下，linearsvc.coef_是所有特征的权重，linearsvc.intercept_是斜率（线性分类）

print(linearsvc.coef_)         # w，所有x 的权值
print(linearsvc.intercept_)    # b，
# 结果是数组，可能是多分类吧，等我研究了多分类再来看

画出决策边界，这函数不是很好懂。。很久才看明白。

• meshgrid() 返回了有两个向量定义的方形空间中的所有点的集合。x0是x值，x1是y的值
• ravel() 将向量拉成一行
• c_[] 将向量排列在一起
• contourf() 等高线（没想到还能这样用）

def plot_decision_boundary(model, axis):
    x0, x1 = np.meshgrid(
        np.linspace(axis[0], axis[1], int((axis[1]-axis[0])*100)).reshape(-1, 1),# 600个，影响列数
        np.linspace(axis[2], axis[3], int((axis[3]-axis[2])*100)).reshape(-1, 1),# 600个，影响行数
    )
    # x0 和 x1 被拉成一列，然后拼接成360000行2列的矩阵，表示所有点
    X_new = np.c_[x0.ravel(), x1.ravel()]    # 变成 600 * 600行， 2列的矩阵

    y_predict = model.predict(X_new)   # 二维点集才可以用来预测
    zz = y_predict.reshape(x0.shape)   # (600, 600)

    from matplotlib.colors import ListedColormap
    custom_cmap = ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
    
    plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)
#     print(X_new)

plot_decision_boundary(linearsvc, axis=[-3, 3, -3, 3])
plt.scatter(X_stand[y==0,0], X_stand[y==0,1])
plt.scatter(X_stand[y==1,0], X_stand[y==1,1])
plt.show()

添加上下边界：

• 如注释中所写的f(x,y) = w[0]x1 + w[1]x2 + b是决策函数的形式。+1(或-1) = w[0]x1 + w[1]x2 + b就是上下边界的表达式

def plot_svc_decision_boundary(model, axis):
    x0, x1 = np.meshgrid(
        np.linspace(axis[0], axis[1], int((axis[1]-axis[0])*100)).reshape(-1, 1),# 600个，影响列数
        np.linspace(axis[2], axis[3], int((axis[3]-axis[2])*100)).reshape(-1, 1),# 600个，影响行数
    )
    # x0 和 x1 被拉成一列，然后拼接成360000行2列的矩阵，表示所有点
    X_new = np.c_[x0.ravel(), x1.ravel()]    # 变成 600 * 600行， 2列的矩阵

    y_predict = model.predict(X_new)   # 二维点集才可以用来预测
    zz = y_predict.reshape(x0.shape)   # (600, 600)

    from matplotlib.colors import ListedColormap
    custom_cmap = ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
    
    plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)
    
    # 我终于看懂了！！！！！
    w = model.coef_[0]
    b = model.intercept_[0]
    
    index_x = np.linspace(axis[0], axis[1], 100)
#     f(x,y) = w[0]x1 + w[1]x2 + b
#     1 = w[0]x1 + w[1]x2 + b    上边界
#     -1 = w[0]x1 + w[1]x2 + b   下边界
    y_up = (1-w[0]*index_x - b) / w[1]
    y_down = (-1-w[0]*index_x - b) / w[1]
    
    x_index_up = index_x[(y_up<=axis[3])  & (y_up>=axis[2])]
    x_index_down = index_x[(y_down<=axis[3]) & (y_down>=axis[2])]
    
    y_up = y_up[(y_up<=axis[3])  & (y_up>=axis[2])]
    y_down = y_down[(y_down<=axis[3]) & (y_down>=axis[2])]
    
    plt.plot(x_index_up, y_up, color="black")
    plt.plot(x_index_down, y_down, color="black")

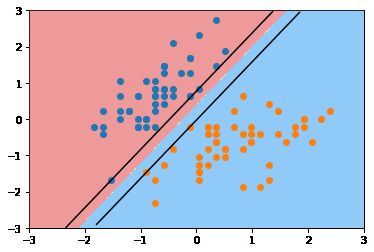
def svc_plot(model, axis=[-3, 3, -3, 3], X_stand, y):
    plot_svc_decision_boundary(model, axis=[-3, 3, -3, 3])
    plt.scatter(X_stand[y==0,0], X_stand[y==0,1])
    plt.scatter(X_stand[y==1,0], X_stand[y==1,1])
    plt.show()

常数C越大，容错空间越小，上下边界越远；常数C越小，容错空间越大，上下边界越远。当C缩小到0.01时，上下边界已经很远了。

# C越小，容错空间越大上下边界应该更远，是的就是这样
linearsvc = LinearSVC(C=0.01)
linearsvc.fit(X_stand, y)
svc_plot(model=linearsvc,axis=[-3, 3, -3, 3], X_stand=X_stand, y=y)

多项式核函数

这里可以手动使用 PolynomialFeature将数据升维，再用LinearSVC进行分类。也可以直接使用SVC指定多项式核函数，即：

• 用LinearSVC，需要用PolynomialFeatures升维
• 用SVC() 指定kernel=poly

准备数据

使用sklearn自带的moon数据

moons = datasets.make_moons(noise=0.15)
X = moons[0]
y = moons[1]

plt.scatter(X[y==0,0], X[y==0, 1])
plt.scatter(X[y==1,0], X[y==1, 1])

使用LinearSVC分类，使用pipeline封装一下

from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler

# 使用Pipeline的一条龙服务
def PolynomialSVC(degree, C=1.0):
    return Pipeline([
        ("poly", PolynomialFeatures(degree=degree)),
        ("std_scaler", StandardScaler()),
        ("linearSVC", LinearSVC(C=C))
    ])

poly_svc = PolynomialSVC(degree=3)
poly_svc.fit(X, y)
poly_svc.predict(X)

plot_decision_boundary(poly_svc, axis=[-1.5, 2.5, -1.0, 1.5])
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])

使用多项式核函数分类：

def PolynomialSVC(degree, C=1):
    return Pipeline([
        ("std_scaler", StandardScaler()),
        ("linearSVC", SVC(kernel="poly", C=C))
    ])

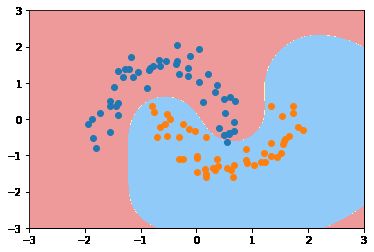
poly_svc2 = PolynomialSVC(3)
poly_svc2.fit(X,y)

plot_decision_boundary(poly_svc2, axis=[-1.5, 2.5, -1.0, 1.5])
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])

我也不知道，为什么训练结果不太一样。而且多项式核函数还可以加参数gamma，而多项式核函数中并没有gamma这个参数。。奇怪。

高斯核函数

def SVC_(kernel="rbf", gamma=1):
    return Pipeline([
        ("std_scaler", StandardScaler()),
        ("linearSVC", SVC(kernel="rbf", gamma=gamma))
    ])

svc = SVC_(kernel="rbf", gamma=0.7)
svc.fit(X_stand, y)

plot_decision_boundary(svc, [-3,3,-3,3])
plt.scatter(X_stand[y==0,0], X_stand[y==0,1])
plt.scatter(X_stand[y==1,0], X_stand[y==1,1])

改一下gamma的参数，

• gamma参数越大，高斯分布越窄

svc = SVC_(kernel="rbf", gamma=100)
svc.fit(X_stand, y)

plot_decision_boundary(svc, [-3,3,-3,3])
plt.scatter(X_stand[y==0,0], X_stand[y==0,1])
plt.scatter(X_stand[y==1,0], X_stand[y==1,1])

回归

没想到还能用在回归上，伪造一个三阶函数的数据集：

x = np.linspace(0, 3, 50)
y = x * x + 10 + np.random.uniform(0,2,50)
x = x.reshape(-1,1)
plt.scatter(x,y)

分别用线性、多项式、高斯函数三种核函数分类

from sklearn.svm import SVR
linear_svr = SVR(kernel="linear")
poly_svr = SVR(kernel="poly", degree=4)
rbf_svr = SVR(kernel="rbf")

linear_svr.fit(x,y)
poly_svr.fit(x,y)
rbf_svr.fit(x,y)

print(linear_svr.coef_, linear_svr.intercept_)    # [[2.62357607]] [10.14231851]

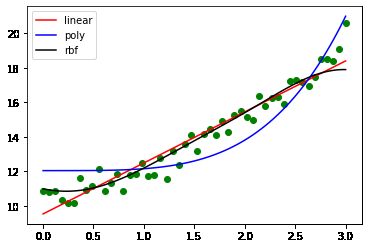
画出三个模型

x_test = np.linspace(0,3,100).reshape(-1,1)
plt.scatter(x,y, color="green")
plt.plot(x_test, linear_svr.predict(x_test), color="red", label="linear")
plt.plot(x_test, poly_svr.predict(x_test), color="blue", label="poly")
plt.plot(x_test, rbf_svr.predict(x_test), color="black", label="rbf")
plt.legend()

借鉴自下面两位大佬的文章：

• sklearn.svm/SVC/SVR/拉格朗日乘子法
• 【机器学习详解】SVM解回归问题