Python实现分类器性能度量(混淆矩阵,正确率,准确率,召回率,ROC,AUC)
1.混淆矩阵
对于二分类问题,可将样例根据其真实类别与分类器预测类别的组合划分为:
真正例(true positive):将一个正例正确判断为正例
假正例(false positive):将一个反例错误判断为正例
真反例(true negative):将一个反例正确判断为反例
假反例(false negative):将一个正例错误判断为反例
令TP、FP、TN、FN分别表示对应的样例数,这四个指标构成了分类结果的混淆矩阵:
| 正例(预测结果) | 反例(预测结果) | |
| 正例(真实情况) | TP(真正例) | FN(假反例) |
| 反例(真实情况) | FP(假正例) | TN(真反例) |
样例总数 = TP + FP + TN + FN
2.正确率(accuracy)
即分类正确的样本数占样本总数的比例:
accuracy = (TP + TN) / (TP + FP + TN + FN)
3.准确率(precision)
即预测为正例的样本中真正为正例的比例:
precision = TP / (TP + FP)
4.召回率(recall)
也称检出率,即真正为正例的样本中正确预测为正例的比例:
recall = TP / (TP + FN)
5.ROC
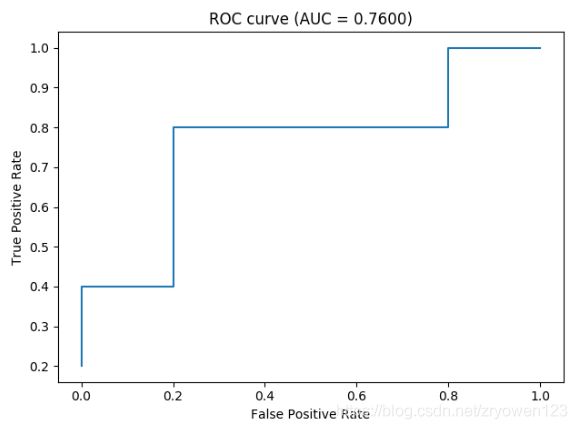
ROC全称“受试者工作特征”曲线。我们根据机器学习的预测评分结果对样例进行排序,按此顺序逐个把样本的分值作为检查为正例的阈值进行预测,计算得到两个重要的指标:真正例率(True Positive Rate, TPR)、假正例率(False Positive Rate, FPR)。以TPR为纵轴,FPR为横轴做图,就得到了“ROC”曲线。
TPR = TP / (TP + FN)
FPR = FP / (TN + FP)
6.AUC
AUC即为ROC曲线下的面积
7.Python实现
import numpy as np
import matplotlib.pyplot as plt
class Performance:
"""
定义一个类,用来分类器的性能度量
"""
def __init__(self, labels, scores, threshold=0.5):
"""
:param labels:数组类型,真实的标签
:param scores:数组类型,分类器的得分
:param threshold:检测阈值
"""
self.labels = labels
self.scores = scores
self.threshold = threshold
self.db = self.get_db()
self.TP, self.FP, self.FN, self.TN = self.get_confusion_matrix()
def accuracy(self):
"""
:return: 正确率
"""
return (self.TP + self.TN) / (self.TP + self.FN + self.FP + self.TN)
def presision(self):
"""
:return: 准确率
"""
return self.TP / (self.TP + self.FP)
def recall(self):
"""
:return: 召回率
"""
return self.TP / (self.TP + self.FN)
def auc(self):
"""
:return: auc值
"""
auc = 0.
prev_x = 0
xy_arr = self.roc_coord()
for x, y in xy_arr:
if x != prev_x:
auc += (x - prev_x) * y
prev_x = x
return auc
def roc_coord(self):
"""
:return: roc坐标
"""
xy_arr = []
tp, fp = 0., 0.
neg = self.TN + self.FP
pos = self.TP + self.FN
for i in range(len(self.db)):
tp += self.db[i][0]
fp += 1 - self.db[i][0]
xy_arr.append([fp / neg, tp / pos])
return xy_arr
def roc_plot(self):
"""
画roc曲线
:return:
"""
auc = self.auc()
xy_arr = self.roc_coord()
x = [_v[0] for _v in xy_arr]
y = [_v[1] for _v in xy_arr]
plt.title("ROC curve (AUC = %.4f)" % auc)
plt.ylabel("True Positive Rate")
plt.xlabel("False Positive Rate")
plt.plot(x, y)
plt.show()
def get_db(self):
db = []
for i in range(len(self.labels)):
db.append([self.labels[i], self.scores[i]])
db = sorted(db, key=lambda x: x[1], reverse=True)
return db
def get_confusion_matrix(self):
"""
计算混淆矩阵
:return:
"""
tp, fp, fn, tn = 0., 0., 0., 0.
for i in range(len(self.labels)):
if self.labels[i] == 1 and self.scores[i] >= self.threshold:
tp += 1
elif self.labels[i] == 0 and self.scores[i] >= self.threshold:
fp += 1
elif self.labels[i] == 1 and self.scores[i] < self.threshold:
fn += 1
else:
tn += 1
return [tp, fp, fn, tn]测试一下:
if __name__ == '__main__':
labels = np.array([1, 1, 0, 1, 1, 0, 0, 0, 1, 0])
scores = np.array([0.9, 0.8, 0.7, 0.6, 0.55, 0.54, 0.53, 0.51, 0.5, 0.4])
p = Performance(labels, scores)
acc = p.accuracy()
pre = p.presision()
rec = p.recall()
print('accuracy: %.2f' % acc)
print('precision: %.2f' % pre)
print('recall: %.2f' % rec)
p.roc_plot()结果为:
accuracy: 0.60
precision: 0.56
recall: 1.00