二维差分【算法推导，图文讲解清晰】

798. 差分矩阵 - AcWing题库

算法推导

二维差分相对一维差分会复杂一点，而且还要结合二维前缀和的一些细节处理

A、B数组角色问题

在差分思想中，构造并不是那么重要，而是其中A、B数组的角色。

我们假想存在一个数组B，输入的A数组是B数组的前缀和——差分思想核心

也就是说：我们对B[i][j] 添加一个数后，从A[i][j]开始一直到A[n][n]都将 添加一个数

所以，这样就很巧妙的将 需要循环处理的，转化成了对B数组的某一个的处理（好好理解这句话！！！看懂这个你就看懂了差分的核心思想）

当然，可能还有一点比较奇怪的是：那怎么解释开始时和输入后的数组呢？

开始时，前缀和数组A（输入的）和B数组都是空的，也都是0，此时是满足前缀和概念的

然后当我们开始往A数组写入数据时，此时B数组是空的，那么此时就A数组好像就并不是B数组的前缀和了！

所以，此时我们需要向B数组对应位置也插入相应的值，只是需要处理的坐标都是i , j

这样就满足了A是B的前缀和的概念了

处理B数组的值

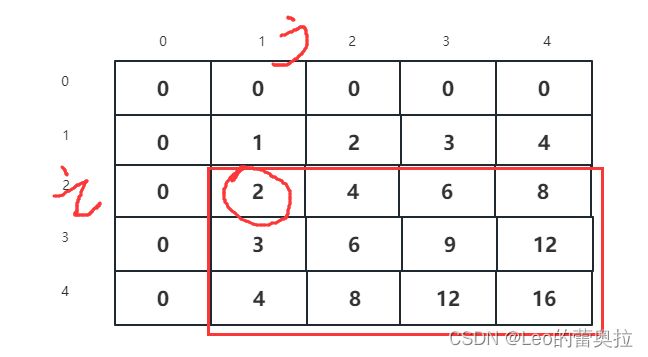
因为A数组是B数组的前缀和，所以当我们对B[i][j]加上某一个常数c后，A数组从[ i, j ]后面都加上了c

具体来说，当i = 2 , j = 1时加上一个常数时，后面（红色框起来的）都加上了一个常数

然而题目所要求的的是，我们在[ x1 , y1 ]到[ x2 , y2 ]范围加上一个常数c即可，所以我们就需要像二维前缀和数组一样减去某些位置的值

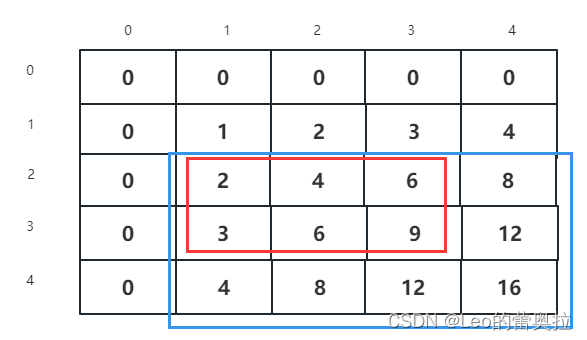
假设，我们只需要计算[2 , 1]到[3 , 3]的数据

也就是只需要对红色框加上常数即可

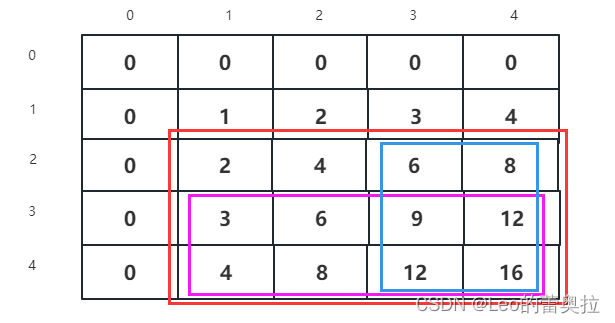
当我们对a[2][1]加上常数c后，从[2 , 1]到[4 , 4]都加上了c，我们需要减去对应的值即可

从图中我们不难看出，我们需要进行

• a[3 , 1] -= c
• a[2 , 3] -= c

但是这里我们会发现会减去两次，所以我们需要对a[3 , 3] += c

抽象总结

• a[2][1] += c
• a[3][1] -= c
• a[2][3] -= c
• a[3][3] += c

这里对应的（x1，y1）和（x2，y2）分别是（2,1）和（3,3）

所以抽象一下，我们就能得到这样一个核心插入逻辑

• b[x1][y1] += c;
• b[x2 + 1][y1] -= c;
• b[x1][y2 + 1] -= c;
• b[x2 + 1][y2 + 1] += c;

结果输出

因为前面我们对于A数组的设计是B数组的前缀和，但是在前面的相关逻辑处理中，我们并没有体现，所以我们需要在结果计算中体现

这里就与前缀和的处理逻辑一样了

            b[i][j] += b[i-1][j] + b[i][j - 1] - b[i - 1][j - 1];

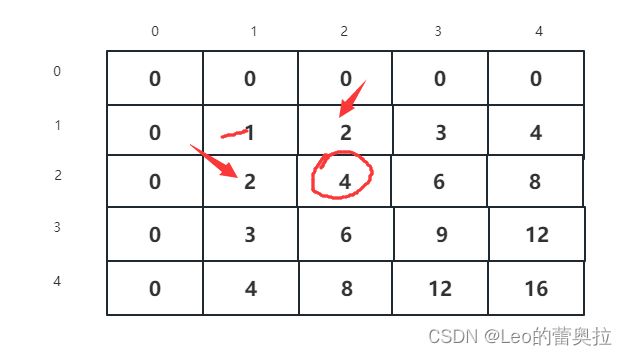
假设，当前我们需要计算[2 , 2]时，我们就需要加上左边和上边的值

但是因为左上角的那个值会被加两次，所以这里就要 加上一个c

代码模板

#include

using namespace std;

int n , m , q;

const int N = 1008;

int a[N][N] , b[N][N];

void insert(int x1, int y1 , int x2 , int y2 , int c){
    b[x1][y1] += c;
    b[x2 + 1][y1] -= c;
    b[x1][y2 + 1] -= c;
    b[x2 + 1][y2 + 1] += c;
}

int main(){
    scanf("%d %d %d" , &n  , &m , &q);
  
    for(int i = 1 ; i <= n ; i ++ ){
        for(int j = 1 ; j <= m ; j ++){
            scanf("%d" , &a[i][j]);
            insert(i , j , i , j , a[i][j]);
        }
    }
  
    int x1 , y1 , x2 ,y2 , c;
    while(q --){
        scanf("%d %d %d %d %d",&x1,&y1,&x2,&y2 , &c);
      
        insert(x1 ,y1 , x2 , y2 , c);
    }
  
    for(int i = 1 ; i <= n ; i ++){
        for(int j = 1 ; j <= m ; j ++){
            b[i][j] += b[i-1][j] + b[i][j - 1] - b[i - 1][j - 1];
            cout << b[i][j] << " ";
        }
        cout << endl;
    }
  
    return 0 ;
}