7.2 模拟乘法器及其在运算电路中的应用
模拟乘法器是实现两个模拟量相乘的非线性电子器件，利用它可以方便地实现乘、除、乘方和开方运算电路。此外，由于它还能广泛地应用于广播电视、通讯、仪表和自动控制系统，进行模拟信号的处理，所以发展很快，称为模拟集成电路的重要分支之一。
一、模拟乘法器简介
实现模拟量相乘可以有多种方案，但就集成电路而言，多采用变跨导型电路。
模拟乘法器的符号和等效电路
模拟乘法器有两个输入端，一个输出端，输入及输出均对 “地” 而言，如图7.2.1(a)所示。输入的两个模拟信号是互不相关的物理量，输出电压是它们的乘积，即 u O = k u X u Y ( 7.2.1 ) u_O=ku_Xu_Y\kern 40pt(7.2.1) uO=kuXuY(7.2.1) k k k 为乘积系数，也称乘积增益或标尺因子，其值多为 + 0.1 V − 1 +0.1\,\textrm V^{-1} +0.1V−1 或 − 0.1 V − 1 -0.1\textrm V^{-1} −0.1V−1。
模拟乘法器的等效电路如图（b）所示， r i 1 r_{i1} ri1 和 r i 2 r_{i2} ri2 分别为两个输入端的输入电阻， r o r_o ro 是输出电阻。
理想模拟乘法器应具备如下条件：
（1） r i 1 r_{i1} ri1 和 r i 2 r_{i2} ri2 为无穷大；
（2） r o r_o ro 为零；
（3） k k k 值不随输入信号的幅值和频率而变化；
（4）当 u X u_X uX 或 u Y u_Y uY 为零时 u O u_O uO 为零，电路没有失调电压、电流和噪声。
在上述条件下，无论 u X u_X uX 和 u Y u_Y uY 的波形、幅值、频率、极性如何变化，式（7.2.1）均成立。这里的分析均设模拟乘法器为理想器件。
输入信号 u X u_X uX 和 u Y u_Y uY 的极性有四种可能的组合，在 u X u_X uX 和 u Y u_Y uY 的坐标平面上，分为四个区域，即四个象限，如图7.2.2所示。按照允许输入信号的极性，模拟乘法器有单象限、两象限和四象限之分。
二、变跨导型模拟乘法器的工作原理
变跨导型模拟乘法器利用输入电压控制差分放大电路差分管的发射极电流，使之跨导作相应的变化，从而达到与输入差模信号相乘的目的。
1、差分放大电路的差模传输特性
差分放大电路的差分传输特性是指在差模信号作用下，输出电压与输入电压的函数关系。
在图7.2.3(a)所示差分放大电路中， u X u_X uX 为差模输入电压， u X = u B E 1 − u B E 2 ( 7.2.2 ) u_X=u_{BE1}-u_{BE2}\kern 40pt(7.2.2) uX=uBE1−uBE2(7.2.2)差分管的跨导 g m = I E Q U T = I 0 2 U T ( 7.2.3 ) g_m=\frac{I_{EQ}}{U_T}=\frac{I_0}{2U_T}\kern 40pt(7.2.3) gm=UTIEQ=2UTI0(7.2.3)恒流源电流 I 0 = i E 1 + i E 2 ≈ I S e u B E 1 U T + I S e u B E 2 U T = I S e u B E 2 U T ( 1 + e u B E 1 − u B E 2 U T ) = i E 2 ( 1 + e u B E 1 − u B E 2 U T ) I_0=i_{E1}+i_{E2}\kern 60pt\\\kern 3pt\approx I_Se^{\frac{\textstyle u_{\scriptscriptstyle BE1}}{U_T}}+I_Se^{\frac{\textstyle u_{\scriptscriptstyle BE2}}{U_T}}\\\kern 40pt= I_Se^{\frac{\textstyle u_{\scriptscriptstyle BE2}}{U_T}}\Big(1+e^{{\frac{\textstyle u_{\scriptscriptstyle BE1}-u_{\scriptscriptstyle BE2}}{U_T}}}\Big)\\\kern 15pt=i_{\scriptscriptstyle E2}\Big(1+e^{{\frac{\textstyle u_{\scriptscriptstyle BE1}-u_{\scriptscriptstyle BE2}}{U_T}}}\Big) I0=iE1+iE2≈ISeUTuBE1+ISeUTuBE2=ISeUTuBE2(1+eUTuBE1−uBE2)=iE2(1+eUTuBE1−uBE2)因此 T 2 T_2 T2 管的发射极电流 i E 2 = I 0 1 + e + u X U T i_{\scriptscriptstyle E2}=\frac{I_0}{1+e^{\frac{+\textstyle u_{\scriptscriptstyle X}}{U_T}}} iE2=1+eUT+uXI0同理可得 T 1 T_1 T1 管的发射极电流 i E 1 = I 0 1 + e − u X U T i_{\scriptscriptstyle E1}=\frac{I_0}{1+e^{\frac{-\textstyle u_{\scriptscriptstyle X}}{U_T}}} iE1=1+eUT−uXI0由于 i E 1 − I 0 2 = I 0 2 ( 2 1 + e − u X U T − 1 ) = I 0 2 ⋅ 1 − e − u X U T 1 + e − u X U T = I 0 2 ⋅ e u X 2 U T − e − u X 2 U T e u X 2 U T + e − u X 2 U T = I 0 2 th u X 2 U T i_{\scriptscriptstyle E1}-\frac{I_0}{2}=\frac{I_0}{2}\Big(\frac{2}{1+e^{\frac{-\textstyle u_{\scriptscriptstyle X}}{U_T}}}-1\Big)\\\kern 23pt=\frac{I_0}{2}\cdot\frac{1-e^{\frac{-\textstyle u_{\scriptscriptstyle X}}{U_T}}}{1+e^{\frac{-\textstyle u_{\scriptscriptstyle X}}{U_T}}}\\\kern 42pt=\frac{I_0}{2}\cdot\frac{e^{\frac{\textstyle u_{\scriptscriptstyle X}}{2U_T}}-e^{-\frac{\textstyle u_{\scriptscriptstyle X}}{2U_T}}}{e^{\frac{\textstyle u_{\scriptscriptstyle X}}{2U_T}}+e^{-\frac{\textstyle u_{\scriptscriptstyle X}}{2U_T}}}\\\kern 8pt=\frac{I_0}{2}\th\frac{u_{\scriptscriptstyle X}}{2U_T} iE1−2I0=2I0(1+eUT−uX2−1)=2I0⋅1+eUT−uX1−eUT−uX=2I0⋅e2UTuX+e−2UTuXe2UTuX−e−2UTuX=2I0th2UTuX i E 2 − I 0 2 = I 0 2 ( 2 1 + e u X U T − 1 ) = I 0 2 ⋅ 1 − e u X U T 1 + e u X U T = I 0 2 ⋅ e − u X 2 U T − e u X 2 U T e − u X 2 U T + e u X 2 U T = − I 0 2 th u X 2 U T i_{\scriptscriptstyle E2}-\frac{I_0}{2}=\frac{I_0}{2}\Big(\frac{2}{1+e^{\frac{\textstyle u_{\scriptscriptstyle X}}{U_T}}}-1\Big)\\\kern 20pt=\frac{I_0}{2}\cdot\frac{1-e^{\frac{\textstyle u_{\scriptscriptstyle X}}{U_T}}}{1+e^{\frac{\textstyle u_{\scriptscriptstyle X}}{U_T}}}\\\kern 42pt=\frac{I_0}{2}\cdot\frac{e^{-\frac{\textstyle u_{\scriptscriptstyle X}}{2U_T}}-e^{\frac{\textstyle u_{\scriptscriptstyle X}}{2U_T}}}{e^{-\frac{\textstyle u_{\scriptscriptstyle X}}{2U_T}}+e^{\frac{\textstyle u_{\scriptscriptstyle X}}{2U_T}}}\\\kern 14pt=-\frac{I_0}{2}\th\frac{u_{\scriptscriptstyle X}}{2U_T} iE2−2I0=2I0(1+eUTuX2−1)=2I0⋅1+eUTuX1−eUTuX=2I0⋅e−2UTuX+e2UTuXe−2UTuX−e2UTuX=−2I0th2UTuX其中 th x = e x − e − x e x + e − x \th x=\displaystyle\frac{e^x-e^{-x}}{e^x+e^{-x}} thx=ex+e−xex−e−x，是双曲正切函数。因此， i C 1 − i C 2 ≈ i E 1 − i E 2 = I 0 th u X 2 U T ( 7.2.4 ) i_{\scriptscriptstyle C1}-i_{\scriptscriptstyle C2}\approx i_{\scriptscriptstyle E1}-i_{\scriptscriptstyle E2}=I_0\th\frac{\textstyle u_{\scriptscriptstyle X}}{2U_T}\kern 20pt(7.2.4) iC1−iC2≈iE1−iE2=I0th2UTuX(7.2.4)当 u X < < 2 U T u_{\scriptscriptstyle X}<<2U_T uX<<2UT（ 约 2 × 26 mV 2\times26\,\textrm{mV} 2×26mV ）时，有 i C 1 − i C 2 ≈ I 0 u X 2 U T = g m u X i_{\scriptscriptstyle C1}-i_{\scriptscriptstyle C2}\approx I_0\frac{u_{\scriptscriptstyle X}}{2U_T}=g_mu_{\scriptscriptstyle X} iC1−iC2≈I02UTuX=gmuX输出电压 u O = − ( i C 1 − i C 2 ) R c ≈ − I 0 u X 2 U T ⋅ R c = − g m R c u X ( 7.2.5 ) u_{\scriptscriptstyle O}=-(i_{\scriptscriptstyle C1}-i_{C2})R_c\approx-I_0\frac{u_{\scriptscriptstyle X}}{2U_T}\cdot R_c=-g_mR_cu_{\scriptscriptstyle X}\kern 20pt(7.2.5) uO=−(iC1−iC2)Rc≈−I02UTuX⋅Rc=−gmRcuX(7.2.5)因而电路的差模电压传输特性如图7.2.3(b)所示。
2、可控恒流源差分放大电路的乘法特性
在图7.2.4所示差分放大电路中， i C 3 = I ≈ u Y − u B E 3 R e i_{\scriptscriptstyle C3}=I\approx\frac{u_{\scriptscriptstyle Y}-u_{\scriptscriptstyle BE3}}{R_e} iC3=I≈ReuY−uBE3代入式（7.2.5）可得 u O = − u Y − u B E 3 R e ⋅ u X 2 U T ⋅ R c ( 7.2.6 ) u_{\scriptscriptstyle O}=-\frac{u_{\scriptscriptstyle Y}-u_{\scriptscriptstyle BE3}}{R_e}\cdot\frac{u_{\scriptscriptstyle X}}{2U_T}\cdot R_c\kern 20pt(7.2.6) uO=−ReuY−uBE3⋅2UTuX⋅Rc(7.2.6)若 u Y > > u B E 3 u_{\scriptscriptstyle Y}>>u_{\scriptscriptstyle BE3} uY>>uBE3，则 u O ≈ − R c 2 U T R e ⋅ u X u Y = k u X u Y ( 7.2.7 ) u_{\scriptscriptstyle O}\approx-\frac{R_c}{2U_TR_e}\cdot u_{\scriptscriptstyle X}u_{\scriptscriptstyle Y}=ku_{\scriptscriptstyle X}u_{\scriptscriptstyle Y}\kern 15pt(7.2.7) uO≈−2UTReRc⋅uXuY=kuXuY(7.2.7)式中 u X u_{\scriptscriptstyle X} uX 可正可负，但 u Y u_{\scriptscriptstyle Y} uY 必须大于零，故图7.2.4所示为两象限模拟乘法器。电路有如下明确的缺点：
（1）式（7.2.6）表明， u Y u_{\scriptscriptstyle Y} uY 的值越小，运算误差越大；
（2）式（7.2.7）表明， u O u_{\scriptscriptstyle O} uO 与 U T U_T UT 有关，即 k k k 与温度有关；
（3）电路只能工作在两象限。
3、四象限变跨导型模拟乘法器
图7.2.5所示为双平衡四象限变跨导型模拟乘法器。通过对图7.2.3所示电路的分析，得到的式（7.2.4）适用于图7.2.5所示电路，因而 i 1 − i 2 ≈ i 5 th u X 2 U T ( 7.2.8 ) i_1-i_2\approx i_5\th\frac{u_{\scriptscriptstyle X}}{2U_T}\kern 20pt(7.2.8) i1−i2≈i5th2UTuX(7.2.8) i 4 − i 3 ≈ i 6 th u X 2 U T ( 7.2.9 ) i_4-i_3\approx i_6\th\frac{u_{\scriptscriptstyle X}}{2U_T}\kern 20pt(7.2.9) i4−i3≈i6th2UTuX(7.2.9) i 5 − i 6 ≈ I th u Y 2 U T ( 7.2.10 ) i_5-i_6\approx I\th\frac{u_{\scriptscriptstyle Y}}{2U_T}\kern 28pt(7.2.10) i5−i6≈Ith2UTuY(7.2.10) i O 1 − i O 2 = ( i 1 + i 3 ) − ( i 4 + i 2 ) = ( i 1 − i 2 ) − ( i 4 − i 3 ) i_{\scriptscriptstyle O1}-i_{\scriptscriptstyle O2}=(i_1+i_3)-(i_4+i_2)=(i_1-i_2)-(i_4-i_3) iO1−iO2=(i1+i3)−(i4+i2)=(i1−i2)−(i4−i3)将式（7.2.8）、（7.2.9）、（7.2.10）代入上式，得 i O 1 − i O 2 ≈ ( i 5 − i 6 ) th u X 2 U T ≈ I ( th u Y 2 U T ) ( th u X 2 U T ) i_{\scriptscriptstyle O1}-i_{\scriptscriptstyle O2}\approx(i_5-i_6)\th\frac{u_{\scriptscriptstyle X}}{2U_T}\approx I\big(\th\frac{u_{\scriptscriptstyle Y}}{2U_T}\big)\big(\th\frac{u_{\scriptscriptstyle X}}{2U_T}\big) iO1−iO2≈(i5−i6)th2UTuX≈I(th2UTuY)(th2UTuX)当 u X < < 2 U T u_{\scriptscriptstyle X}<<2U_T uX<<2UT，且 u Y < < 2 U T u_{\scriptscriptstyle Y}<<2U_T uY<<2UT 时， i O 1 − i O 2 ≈ I 4 U T 2 ⋅ u X u Y i_{\scriptscriptstyle O1}-i_{\scriptscriptstyle O2}\approx\frac{I}{4U^2_T}\cdot u_{\scriptscriptstyle X}u_{\scriptscriptstyle Y} iO1−iO2≈4UT2I⋅uXuY所以输出电压 u O = − ( i O 1 − i O 2 ) R c ≈ − I 4 U T 2 u X u Y = k u X u Y ( 7.2.11 ) u_O=-(i_{\scriptscriptstyle O1}-i_{\scriptscriptstyle O2})R_c\approx-\frac{I}{4U^2_T}u_{\scriptscriptstyle X}u_{\scriptscriptstyle Y}=ku_{\scriptscriptstyle X}u_{\scriptscriptstyle Y}\kern 10pt(7.2.11) uO=−(iO1−iO2)Rc≈−4UT2IuXuY=kuXuY(7.2.11)由于 u X u_{\scriptscriptstyle X} uX 和 u Y u_{\scriptscriptstyle Y} uY 均可正可负，故图7.2.5所示电路为四象限模拟乘法器。它是双端输出形式，可利用图7.2.6所示的集成运算电路，将其转换成单端输出形式。
4、模拟乘法器的性能指标
与集成运放一样，为了衡量模拟乘法器的性能好坏，特别设定一些指标参数。表1中列出主要参数及其典型数值。 表 1 模拟乘法器的主要参数 表1\,\,模拟乘法器的主要参数 表1模拟乘法器的主要参数
| 参数名称 | 单位 | 典型值 | 测试条件 |
|---|---|---|---|
| 输入失调电流 I I O I_{IO} IIO | μA | 0.2 | u X = u Y = 0 V u_{\scriptscriptstyle X}=u_{\scriptscriptstyle Y}=0\,\textrm V uX=uY=0V |
| 输入偏置电流 I B I_B IB | μA | 2.0 | u X = u Y = 0 V u_X=u_Y=0\,\textrm V uX=uY=0V |
| 输出不平衡电流 I O O I_{OO} IOO | μA | 20 | u X = u Y = 0 V u_X=u_Y=0\,\textrm V uX=uY=0V |
| 输出精度 ξ R x ξ R y \xi_{Rx}\xi_{Ry} ξRxξRy | % | 1 ~ 2 | u X = 10 V u_X=10\,\textrm V uX=10V、 u Y = ± 10 V u_Y=±10\,\textrm V uY=±10V 和 u Y = 10 V u_Y=10\,\textrm V uY=10V、 u X = ± 10 V u_X=±10\,\textrm V uX=±10V |
| -3 dB 增益带宽 f b w f_{bw} fbw | MHz | 3.0 | 满刻度位置 |
| 满功率响应 f P f_{\scriptscriptstyle P} fP | kHz | 700 | 满刻度位置 |
| 上升速度 S R SR SR | V/μs | 45 | 满刻度位置 |
| 输入电阻 r i r_i ri | MΩ | 35 |
此外，还有共模输入电压范围、共模增益、输出电阻和矢量误差等。
三、模拟乘法器在运算电路中的应用
模拟乘法器除了自身能够实现两个模拟信号的乘法和平方运算外，还可以和其它电路相配合构成除法、开方、均方根等运算电路。
1、乘方运算电路
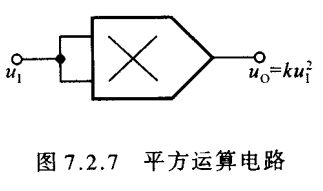
利用四象限模拟乘法器能够实现四象限平方运算电路，如图7.2.7所示。
输出电压 u O = k u I 2 ( 7.2.13 ) u_{\scriptscriptstyle O}=ku^2_{\scriptscriptstyle I}\kern 60pt(7.2.13) uO=kuI2(7.2.13)当 u I u_{\scriptscriptstyle I} uI 为正弦波且 u I = 2 U i sin ω t u_{I}=\sqrt 2U_i\sin\omega t uI=2Uisinωt 时，则 u O = 2 k U i 2 sin 2 ω t = k U i 2 ( 1 − cos 2 ω t ) ( 7.2.14 ) u_{\scriptscriptstyle O}=2kU^2_i\sin^2 \omega t=kU^2_i(1-\cos 2\omega t)\kern 20pt(7.2.14) uO=2kUi2sin2ωt=kUi2(1−cos2ωt)(7.2.14)输出为输入的二倍频电压信号，为了得到纯交流电压，可在输出端加耦合电容，以隔离直流电压。
从理论上将，可以用多个模拟乘法器串联组成 u I u_{\scriptscriptstyle I} uI 的任意次幂的运算电路，图7.2.8(a)、（b）所示分别为 3 次方和 4 次方运算电路。它们的表达式分别为 u O 1 = k 2 u I 3 u_{\scriptscriptstyle O1}=k^2u^3_{\scriptscriptstyle I} uO1=k2uI3 u O 2 = k 2 u I 4 u_{O2}=k^2u^4_{\scriptscriptstyle I} uO2=k2uI4但是，实际上，当串联的模拟乘法器超过 3 个时，运算误差的积累就使得电路的精度变得很差，在要求较高时将不适用。因此，在实现高次幂的乘方运算时，可以考虑采用模拟乘法器与集成对数运算电路和指数运算电路组合而成，如图7.2.9所示。
对数运算电路的输出电压 u O 1 = k 1 ln u I u_{\scriptscriptstyle O1}=k_1\ln u_{\scriptscriptstyle I} uO1=k1lnuI模拟乘法器的输出电压 u O 2 = k 1 k 2 N ln u I u_{\scriptscriptstyle O2}=k_1k_2N\ln u_{\scriptscriptstyle I} uO2=k1k2NlnuI k 2 k_2 k2 为乘积系数。输出电压 u O = k 3 u I k 1 k 2 N = k 3 u I k N ( 7.2.14 ) u_{\scriptscriptstyle O}=k_3u^{k_1k_2N}_{\scriptscriptstyle I}=k_3u^{kN}_{\scriptscriptstyle I}\kern 30pt(7.2.14) uO=k3uIk1k2N=k3uIkN(7.2.14)设 k 1 = 10 k_1=10 k1=10， k 2 = 0.1 V − 1 k_2=0.1\,\textrm V^{-1} k2=0.1V−1，则当 N > 1 N>1 N>1 时，电路实现乘方运算。若 N = 2 N=2 N=2，则电路为平方运算电路；若 N = 10 V N=10\,\textrm V N=10V，则电路为 10 次幂运算电路。
2、除法运算电路
利用反函数型运算电路的基本原理，将模拟乘法器放在集成运放的反馈通路中，便可构成除法运算电路，如图7.2.10所示。与只用集成运放组成的运算电路一样，在用模拟乘法器和集成运放共同构成运算电路时，也必须引入负反馈，据此可确定二者的连接方法。
对于图7.2.10所示电路，必须保证 i 1 = i 2 i_1=i_2 i1=i2，电路引入的才是负反馈。即当 u I 1 > 0 V u_{\scriptscriptstyle I1}>0\,\textrm V uI1>0V 时， u O ′ < 0 V u'_{\scriptscriptstyle O}<0\,\textrm V uO′<0V；而 u I 1 < 0 V u_{\scriptscriptstyle I1}<0\,\textrm V uI1<0V 时， u O ′ > 0 V u'_{\scriptscriptstyle O}>0\,\textrm V uO′>0V。由于 u O u_{\scriptscriptstyle O} uO 与 u I 1 u_{\scriptscriptstyle I1} uI1 反相，故要求 u O ′ u'_{\scriptscriptstyle O} uO′ 与 u O u_{\scriptscriptstyle O} uO 同符号。因此，当模拟乘法器的 k k k 小于零时， u I 2 u_{\scriptscriptstyle I2} uI2 应小于零；而 k k k 大于零时， u I 2 u_{\scriptscriptstyle I2} uI2 应大于零；即 u I 2 u_{\scriptscriptstyle I2} uI2 与 k k k 同符号。同理，若模拟乘法器的输出端通过电阻接集成运放的同相输入端，则为保证电路引入的是负反馈， u I 2 u_{\scriptscriptstyle I2} uI2 与 k k k 的符号应当相反。
在图7.2.10所示电路中。设集成运放为理想运放，则 u N = u P = 0 u_{\scriptscriptstyle N}=u_{\scriptscriptstyle P}=0 uN=uP=0，为虚地， i 1 = i 2 i_1=i_2 i1=i2，即 u I 1 R 1 = − u O ′ R 2 = − k u I 2 u O R 2 \frac{u_{\scriptscriptstyle I1}}{R_1}=-\frac{u'_{\scriptscriptstyle O}}{R_2}=-\frac{ku_{\scriptscriptstyle I2}u_{\scriptscriptstyle O}}{R_2} R1uI1=−R2uO′=−R2kuI2uO整理上式，得出输出电压 u O = − R 2 k R 1 ⋅ u I 1 u I 2 ( 7.2.15 ) u_{\scriptscriptstyle O}=-\frac{R_2}{kR_1}\cdot\frac{u_{\scriptscriptstyle I1}}{u_{\scriptscriptstyle I2}}\kern 40pt(7.2.15) uO=−kR1R2⋅uI2uI1(7.2.15)由于 u I 2 u_{\scriptscriptstyle I2} uI2 的极性受 k k k 的限制，故图7.2.10所示电路为两象限除法运算电路。对于一个确定的除法运算电路，模拟乘法器 k k k 的极性是唯一的，故 u I 2 u_{\scriptscriptstyle I2} uI2 的极性是唯一的，其运算关系式也是唯一的；换言之，若 k k k 或 u I 2 u_{\scriptscriptstyle I2} uI2 的极性变化，则电路的接法应遵循引入负反馈的原则产生相应的变化。
3、开放运算电路
利用乘方运算电路作为集成运放的负反馈通路，就可构成开方运算电路。在除法运算电路中，令 u I 2 = u O u_{\scriptscriptstyle I2}=u_{\scriptscriptstyle O} uI2=uO，就构成平方根运算电路，如图7.2.11所示。
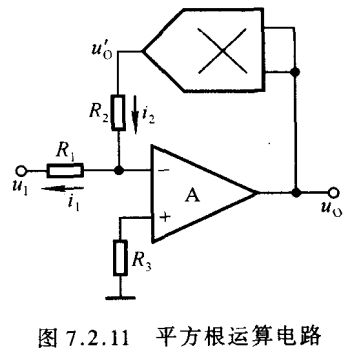
若电路引入的是负反馈，则 u N = u P = 0 u_{\scriptscriptstyle N}=u_{\scriptscriptstyle P}=0 uN=uP=0，为虚地， i 1 = i 2 i_1=i_2 i1=i2，即 − u I R 1 = u O ′ R 2 \frac{-u_{\scriptscriptstyle I}}{R_1}=\frac{u'_{\scriptscriptstyle O}}{R_2} R1−uI=R2uO′ u O ′ = − R 2 R 1 ⋅ u I = k u O 2 ( 7.2.16 ) u'_{\scriptscriptstyle O}=-\frac{R_2}{R_1}\cdot u_{\scriptscriptstyle I}=ku^2_{\scriptscriptstyle O}\kern 30pt(7.2.16) uO′=−R1R2⋅uI=kuO2(7.2.16)故 ∣ u O ∣ = − R 2 u I k R 1 ( 7.2.17 ) |u_{\scriptscriptstyle O}|=\sqrt{-\frac{R_2u_{\scriptscriptstyle I}}{kR_1}}\kern 40pt(7.2.17) ∣uO∣=−kR1R2uI(7.2.17)为了使根号下为正数， u I u_{\scriptscriptstyle I} uI 与 k k k 必须符号相反。因此，由于 u O u_{\scriptscriptstyle O} uO 与 u I u_{\scriptscriptstyle I} uI 极性相反，故当 u I > 0 u_{\scriptscriptstyle I}>0 uI>0、 k < 0 k<0 k<0 时运算关系应为 u O = − − R 2 u I k R 1 ( 7.2.18 ) u_{\scriptscriptstyle O}=-\sqrt{-\frac{R_2u_{\scriptscriptstyle I}}{kR_1}}\kern 35pt(7.2.18) uO=−−kR1R2uI(7.2.18)当 u I < 0 u_{\scriptscriptstyle I}<0 uI<0、 k > 0 k>0 k>0 时运算关系应为 u O = − R 2 u I k R 1 ( 7.2.19 ) u_{\scriptscriptstyle O}=\sqrt{-\frac{R_2u_{\scriptscriptstyle I}}{kR_1}}\kern 39pt(7.2.19) uO=−kR1R2uI(7.2.19)与除法运算电路相同，因为当模拟乘法器选定后 k k k 的极性就唯一地被确定，因此实际电路的运算关系式只可能是（7.2.18）和（7.2.19）中的一个。
在图7.2.11中，若 u I < 0 u_{\scriptscriptstyle I}<0 uI<0、 k > 0 k>0 k>0，则图中所标注的电流方向是在上述条件下电流的实际方向。如果因某种原因使 u I u_{\scriptscriptstyle I} uI 大于零，则必然导致 u O ′ u'_{\scriptscriptstyle O} uO′ 大于零，从而使反馈极性变正，最终使集成运放电路内部的晶体管工作到截止区或饱和区，输出电压接近电源电压，以至于即使 u I u_{\scriptscriptstyle I} uI 变得小于零，集成运放也不能回到线性区，电路不能恢复正常工作，运放出现闭锁或称锁定现象。为了防止闭锁现象的出现，实用电路中常在输出回路串联一个二极管，如图7.2.12所示。
按照平方根运算电路的组成思路，将 3 次方电路作为集成运放的反馈
通路，就可实现立方根运算电路，如图7.2.13所示。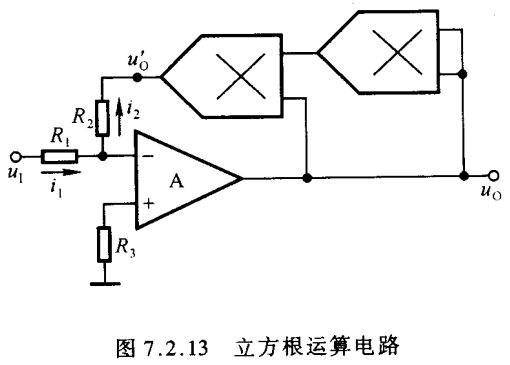
图中有 u O ′ = k 2 u O 3 u'_{\scriptscriptstyle O}=k^2u^3_{\scriptscriptstyle O} uO′=k2uO3由于 k 2 k^2 k2 大于零，且 u O 3 u^3_{\scriptscriptstyle O} uO3 与 u I u_{\scriptscriptstyle I} uI 反相，所以不管 k k k 值为正还是为负，电路均引入了负反馈。电路中 u N = u P = 0 u_{\scriptscriptstyle N}=u_{\scriptscriptstyle P}=0 uN=uP=0，为虚地， i 1 = i 2 i_1=i_2 i1=i2，即 u I R 1 = − u O ′ R 2 \frac{u_{\scriptscriptstyle I}}{R_1}=-\frac{u'_{\scriptscriptstyle O}}{R_2} R1uI=−R2uO′ u O ′ = − R 2 R 1 ⋅ u I = k 2 u O 3 u'_{\scriptscriptstyle O}=-\frac{R_2}{R_1}\cdot u_{\scriptscriptstyle I}=k^2u^3_{\scriptscriptstyle O} uO′=−R1R2⋅uI=k2uO3整理，可得 u O = − R 2 k 2 R 1 ⋅ u I 3 ( 7.2.20 ) u_{\scriptscriptstyle O}=\sqrt[3]{-\frac{R_2}{k^2R_1}\cdot u_{\scriptscriptstyle I}}\kern 30pt(7.2.20) uO=3−k2R1R2⋅uI(7.2.20)与乘方运算电路相类似，当多个模拟乘法器串联实现高次根的运算时，将产生较大的误差。因此，为了提高精度，也可采用如图7.2.9所示电路。从式（7.2.14）可以看出，若 k 1 = 10 k_1=10 k1=10， k 2 = 0.1 V − 1 k_2=0.1\,\textrm V^{-1} k2=0.1V−1，则 k = 1 k=1 k=1；故 N < 1 N<1 N<1 时，电路为开方运算电路。当 N = 0.1 N=0.1 N=0.1 时， u O = k 3 u I 10 u_{\scriptscriptstyle O}=k_3\sqrt[10]{u_{\scriptscriptstyle I}} uO=k310uI；当 N = 0.5 N=0.5 N=0.5 时， u O = k 3 u I u_{\scriptscriptstyle O}=k_3\sqrt{u_{\scriptscriptstyle I}} uO=k3uI。
【例7.2.1】运算电路如图7.2.14所示。已知模拟乘法器的运算关系式为 u O ′ = k u X u Y = − 0.1 V − 1 u X u Y u'_{\scriptscriptstyle O}=ku_{\scriptscriptstyle X}u_{\scriptscriptstyle Y}=-0.1\,\textrm V^{-1}u_{\scriptscriptstyle X}u_{\scriptscriptstyle Y} uO′=kuXuY=−0.1V−1uXuY。
（1）电路对 u I 3 u_{\scriptscriptstyle I3} uI3 的极性是否有要求，简述理由；
（2）求解电路的运算关系式。
解： （1）只有电路中引入负反馈，才能实现运算。而只有 u I 1 u_{\scriptscriptstyle I1} uI1 与 u O ′ u'_{\scriptscriptstyle O} uO′ 符号相反，电路引入的才是负反馈；已知 u O u_{\scriptscriptstyle O} uO 与 u I 1 u_{\scriptscriptstyle I1} uI1 反相，故 u O ′ u'_{\scriptscriptstyle O} uO′ 应与 u O u_{\scriptscriptstyle O} uO 同符号。因为 k < 0 k<0 k<0，所以 u I 3 u_{\scriptscriptstyle I3} uI3 应小于零。
（2） P \textrm P P 点电位 u P = R 2 R 1 + R 2 ⋅ u I 2 = u N u_{\scriptscriptstyle P}=\frac{R_2}{R_1+R_2}\cdot u_{\scriptscriptstyle I2}=u_{\scriptscriptstyle N} uP=R1+R2R2⋅uI2=uN N \textrm N N 点的电流方程为 u I 1 − u N R 1 = u N − u O ′ R 2 \frac{u_{\scriptscriptstyle I1}-u_{\scriptscriptstyle N}}{R_1}=\frac{u_{\scriptscriptstyle N}-u'_{\scriptscriptstyle O}}{R_2} R1uI1−uN=R2uN−uO′将 u N u_{\scriptscriptstyle N} uN 的表达式代入上式，整理得出 u O ′ = R 2 R 1 ( u I 2 − u I 1 ) = k u O u I 3 u'_{\scriptscriptstyle O}=\frac{R_2}{R_1}(u_{\scriptscriptstyle I2}-u_{\scriptscriptstyle I1})=ku_{\scriptscriptstyle O}u_{\scriptscriptstyle I3} uO′=R1R2(uI2−uI1)=kuOuI3所以输出电压 u O = R 2 k R 1 ⋅ u I 2 − u I 1 u I 3 = 100 ⋅ u I 1 − u I 2 u I 3 u_{\scriptscriptstyle O}=\frac{R_2}{kR_1}\cdot \frac{u_{\scriptscriptstyle I2}-u_{\scriptscriptstyle I1}}{u_{\scriptscriptstyle I3}}=100\cdot\frac{u_{\scriptscriptstyle I1}-u_{\scriptscriptstyle I2}}{u_{\scriptscriptstyle I3}} uO=kR1R2⋅uI3uI2−uI1=100⋅uI3uI1−uI2